1289. 下降路径最小和 II

题目描述：

给你一个 n x n 整数矩阵 grid ，请你返回 非零偏移下降路径 数字和的最小值。

非零偏移下降路径 定义为：从 grid 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

示例 1：

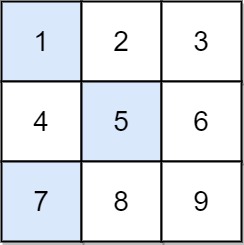
输入：grid = [[1,2,3],[4,5,6],[7,8,9]]
输出：13
解释：
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。

示例 2：

输入：grid = [[7]]
输出：7

提示：

n == grid.length == grid[i].length
1 <= n <= 200
-99 <= grid[i][j] <= 99

实现代码与解析：

动态规划

class Solution {
public:int minFallingPathSum(vector<vector<int>>& grid) {int n = grid.size(), m = grid[0].size();vector<vector<int>> f(n,vector<int>(m, 0x3f3f3f3f));for (int i = 0; i < m; i++)f[0][i] = grid[0][i];for (int i = 1; i < n; i++)for (int j = 0; j < m; j++)for (int k = 0; k < m; k++){if (j == k) continue;f[i][j] = min(f[i][j], f[i - 1][k] + grid[i][j]);}int res = 0x3f3f3f3f;for (int i = 0; i < m; i++)res = min(res, f[n - 1][i]);// for (int i = 0; i < n; i++)// {//     for (int j = 0; j < m; j++)//     {//         cout << f[i][j] << " ";//     }//     cout << endl;// }      return res;}
};