1.前言
创始人 :Duranton and Overman(2005)
目前应用较多的产业集聚度量指数主要基于两类,一是根据不同空间地理单元中产业经济规模的均衡性进行构造,如空间基尼系数与EG指数;二是基于微观企业地理位置信息形成的产业空间分布进行构造,其中代表性方法是DO指数。DO指数旨在利用行业内企业的微观地理位置信息,通过计算企业两两之间的地理距离,得到经济规模加权的企业间距离密度分布,从而获得产业集聚程度关于空间距离的函数。另一方面,通过随机化处理样本企业位置进行的反事实实验可以帮助构造DO指数的假设检验问题与置信区间,DO指数的统计性质更完备。

图像理解
举个具体的例子,假设在某个城市中心,有很多大型科技公司总部设在相邻的几个街区里,每家公司都有成千上万的员工,而城郊则散布着一些小型初创公司。DO指数分析会发现,城市中心区域由于大公司密集且相互之间距离近,加上它们的经济规模大,在计算中占比重高,因此这个区域的DO指数会显示高度的产业集聚。相比之下,城郊的小型公司虽然数量可能不少,但由于它们分散且经济规模小,导致该区域的DO指数较低,反映产业集聚程度较弱。这样,政策制定者或者投资者就可以通过DO指数来识别和理解经济活动的地理分布特征。
再来一个例子
DO指数是一种衡量产业集聚现象的空间分析工具,它通过分析一个行业中不同企业之间的相对位置和聚集情况来评估产业的区域集中度。简单来说,就是看看哪些地方的企业扎堆在一起,以及这些集群的紧密程度如何。
想象一下,你在一个地图上标出所有咖啡店的位置,这些咖啡店就代表了某个行业的企业。DO指数会计算每两家咖啡店之间的距离,并且考虑到每家咖啡店的大小或重要性(比如销售额、员工数量等,这就是经济规模加权),来决定它们在计算中的影响力。如果很多大咖啡店都紧挨着开在一起,那么这个地区的DO指数就会比较高,意味着这里有一个很强的咖啡产业集聚区。
2.实现步骤
step1:计算核密度函数
假定行业 I I I存在n家企业,运营每家企业的经纬度数据,可以估计 n ( n − 1 ) / 2 n(n-1)/2 n(n−1)/2个俩俩企业的空间距离。计算两两企业彼此距离的核密度估计公式:
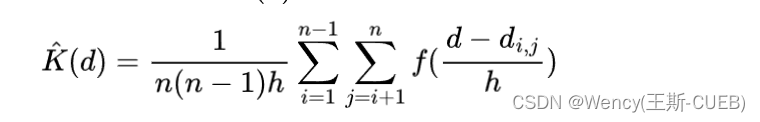
- d d d两两企业的空间距离
- d i j d_{ij} dij企业 i i i和企业 j j j的距离值
- f f f是高斯核密度函数
- h h h是带宽
考虑到企业规模大小会明显影响企业的分布特征,所以本文采用企业就业人数作为规模的权重进入核密度函数,加入权重后的公式:
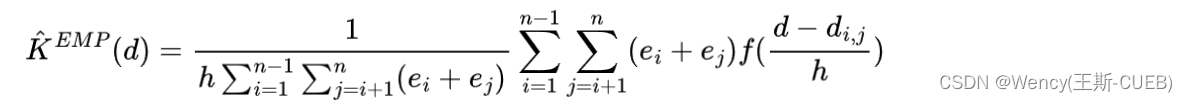
- e i 和 e j e_i和e_j ei和ej企业 i i i和 j j j的就业人数。
step2:反事实实验
为了识别行业 I I I的空间分布模式,在计算该行业两两企业彼此距离的核密度函数后,再将其与无约束条件下企业随机分布假定的核密度函数进行比较。
将考察区域所有企业的位置信息表示为总集 S S S,从中随机地抽取 n n n家企业位置数据代替行业 I I I 的企业进行空间分布的模拟 ,运用这 n n n个模拟的经纬度数据, 再计算出一次反事实的核密度函数。重复反事实实验 1000 次。
step3:构造置信区间
构造置信区间。根据固定距离 d d d,获得的行业 I I I的 1000 次反事实的核密度按升序进行排序,并选择 5%与 95%作为置信区间的下限与上限,伴随着距离的增加可得到置信带,该置信带一般被称为局部置信区间。
3.代码实现
下面是基于python实现的代码。
但是是不含加权版本。
import pandas as pd
from scipy.spatial.distance import pdist, squareform# 假设我们有一个数据框,列名为'Company', 'Latitude', 'Longitude', 'EconomicSize'
# 其中'EconomicSize'代表每个公司的经济规模(可以是销售额、员工数等)
data = {'Company': ['Company A', 'Company B', 'Company C', 'Company D'],'Latitude': [40.7128, 40.7129, 40.7282, 40.7088], # 以纽约市附近为例'Longitude': [-74.0060, -74.0059, -73.9946, -74.0102],'EconomicSize': [1000, 2000, 1500, 3000] # 仅为示例数值
}df = pd.DataFrame(data)# 将经纬度转换为可以用于距离计算的格式
coords = df[['Latitude', 'Longitude']].values# 计算所有企业两两之间的距离矩阵
dist_matrix = pdist(coords, metric='euclidean')# 将距离矩阵转换为方阵,便于后续处理
dist_matrix_square = squareform(dist_matrix)# 这里简化处理,没有直接进行经济规模加权,实际应用中应根据'EconomicSize'调整距离值
# 例如,可以通过乘以每个公司的'EconomicSize'来加权,但这需要更复杂的处理来确保可比性# 简化示例:计算平均距离作为基础的"密度"指标(这不是真正的DO指数,仅作说明)
average_distance = dist_matrix_square.mean()print(f"简化计算的平均距离(非严格DO指数): {average_distance}")





![[Unity常见小问题]打包ios后无法修改模型透明度](https://img-blog.csdnimg.cn/direct/99a63fd3c84040c5ba841a02c2714f30.png)