C. Assembly via Remainders

思路:
我们可以注意到,数组的长度只有 500 500 500 ,并且每个数的大小都在 500 500 500 以内,再看向这题,容易知道,当第一个数确定之后,之后所有的数字都会确定下来,我们枚举第一个数,然后得到整个序列,去判断序列是否合法即可。
#include <bits/stdc++.h>using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
typedef pair<int, int> pll;
typedef array<ll, 3> p3;
// int mod = 998244353;
const int maxv = 4e6 + 5;
// #define endl "\n"void solve()
{ int n;cin>>n;vector<int> a(n);for(int i=1;i<n;i++) cin>>a[i];vector<int> ans(n);for(int i=1;i<=500+5;i++){ans[0]=i;for(int j=1;j<n;j++) ans[j]=ans[j-1]+a[j];int f=1;for(int j=1;j<n;j++){if(ans[j]%ans[j-1]!=a[j]){f=0;break;}}if(f){for(auto x: ans) cout<<x<<" ";cout<<endl;return ;}}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;cin >> t;while (t--){solve();}system("pause");return 0;
}
D. Permutation Game

思路:
容易知道,最优解一定是走到某个格子然后呆在该格子上即可,所以我们可以直接枚举走到的格子,然后取最大值。
#include <bits/stdc++.h>using namespace std;
const int N = 2e5 + 5;
typedef long long ll;
typedef pair<int, int> pll;
typedef array<ll, 3> p3;
// int mod = 998244353;
const int maxv = 4e6 + 5;
#define endl "\n"vector<int> e[N];
vector<ll> a(N);
int n,k;void add(int u,int v){e[u].push_back(v);
}bool st1[N],st2[N];
ll ans1=0,ans2=0;
void dfs1(int x,int time,ll sum)
{ll res=0;st1[x]=1;res=sum+a[x]*time;ans1=max(ans1,res);for(auto u: e[x]){if(st1[u]) continue;if(time==1) return ;dfs1(u,time-1,sum+a[x]);}
}
void dfs2(int x,int time,ll sum)
{ll res=0;st2[x]=1;res=sum+a[x]*time;ans2=max(ans2,res);for(auto u: e[x]){if(st2[u]) continue;if(time==1) return ;dfs2(u,time-1,sum+a[x]);}
}void solve()
{ int s1,s2;cin>>n>>k>>s1>>s2;// k=min(k,n);memset(st1,0,sizeof st1);memset(st2,0,sizeof st2);ans1=ans2=0;for(int i=1;i<=n;i++) e[i].clear();vector<int> p(n+5);for(int i=1;i<=n;i++){cin>>p[i];add(i,p[i]);}for(int i=1;i<=n;i++) cin>>a[i];// cin>>s1>>s2;dfs1(s1,k,0);dfs2(s2,k,0);// cout<<ans1<<" "<<ans2<<endl;if(ans1>ans2) cout<<"Bodya"<<endl;else if(ans1<ans2 ) cout<<"Sasha"<<endl;else cout<<"Draw"<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;cin >> t;while (t--){solve();}system("pause");return 0;
}
E. Cells Arrangement

思路:
**构造没什么好说的。
#include <bits/stdc++.h>using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
typedef pair<int, int> pll;
typedef array<ll, 3> p3;
// int mod = 998244353;
const int maxv = 4e6 + 5;
// #define endl "\n"void solve()
{ int n;cin>>n;if(n==2){cout<<1<<" "<<1<<endl;cout<<1<<" "<<2<<endl;}else{for(int i=1;i<=n;i++){if(i==n-1){cout<<n-1<<" "<<n<<endl;}else cout<<i<<" "<<i<<endl;}}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;cin >> t;while (t--){solve();}system("pause");return 0;
}
F. Equal XOR Segments

思路
题目要求我们把给定的区间划分成 k k k 个,保证每一部分的异或值都相同, q q q 次询问,涉及到多次询问,还有区间异或问题,我们很容易想到,需要把异或前缀和数组给处理出来。
进而,我们考虑最简单的一种情况,即,整个区间的异或和为 0 0 0 时,这时候肯定是一个好数组,那么若区间异或和不为 0 0 0 ,这种时候,我们肯定只能把数组划分成奇数段,同时我们也会发现,当 k = 3 , 5 , 7 , 9 k=3,5,7,9 k=3,5,7,9 等等都是等效的,拿 5 5 5 来举例,我们可以将两个合并成一个 0 0 0 ,然后这样就只剩下三个部分。所以综上所述,这题只存在划分成两段或者是三段的情况。
再来考虑三段的情况如何进行处理:
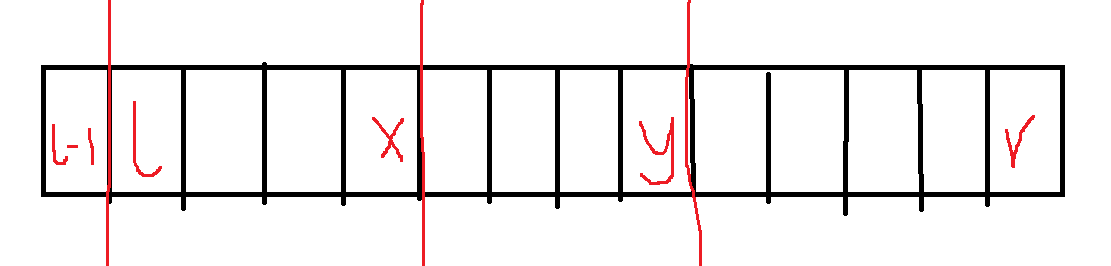
如图,很容易得到, s [ x ] = s [ r ] s[x]=s[r] s[x]=s[r], s [ l − 1 ] = s [ y ] s[l-1]=s[y] s[l−1]=s[y],所以我们可以把前缀异或值相同的下标放入一个桶中,然后我们去二分查找对应的 x , y x,y x,y 是否合法即可,即 l ≤ x < y ≤ r − 1 l\leq x<y\leq r-1 l≤x<y≤r−1。
#include <bits/stdc++.h>using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
typedef pair<int, int> pll;
typedef array<ll, 3> p3;
// int mod = 998244353;
const int maxv = 4e6 + 5;
#define endl "\n"void solve()
{ int n,q;cin>>n>>q;vector<ll> a(n+5),s(n+5);map<ll,vector<int> > mp;mp[0].push_back(0);for(int i=1;i<=n;i++){cin>>a[i];s[i]=s[i-1]^a[i];mp[s[i]].push_back(i);}while(q--){int l,r;cin>>l>>r;if((s[l-1]^s[r])==0){cout<<"YES"<<endl;continue;}auto &v1=mp[s[l-1]];auto &v2=mp[s[r]];int y=lower_bound(v1.begin(),v1.end(),r)-v1.begin()-1;int x=lower_bound(v2.begin(),v2.end(),l)-v2.begin();if(y==v1.size()||y<0||x<0||x==v2.size()){cout<<"NO"<<endl;continue;}if(v1[y]<r&&v2[x]>=l&&v1[y]>v2[x]){cout<<"YES"<<endl;}else cout<<"NO"<<endl;}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;cin >> t;while (t--){solve();}system("pause");return 0;
}
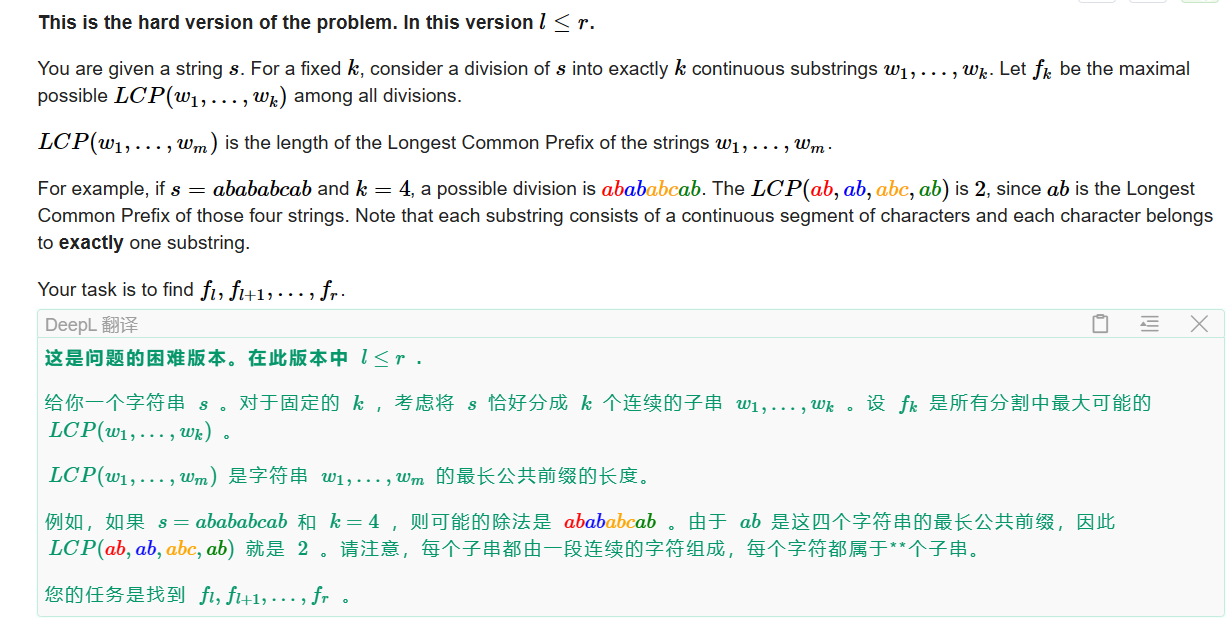
G2. Division + LCP (hard version)
思路:
首先考虑简单版本,即 l = r l=r l=r 的情况,首先我们对整个字符串求出其 z z z 函数,其表示为从当前位置 i i i 开始与整个字符串 s s s 的最长公共前缀,那么接下来我们可以去二分 l c p lcp lcp 的长度,得到二分后的段数 c n t cnt cnt ,然后将 c n t cnt cnt 和 l l l ,进行比较即可,很明显这个东西具有单调性,当我们二分的长度越小时,得到的 c n t cnt cnt 一定是越大的。
#include <bits/stdc++.h>using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
typedef pair<int, int> pll;
typedef array<ll, 3> p3;
// int mod = 998244353;
const int maxv = 4e6 + 5;
// #define endl "\n"vector<int> z_algorithm(const string &s)
{int n = s.size();vector<int> a(n);a[0] = n;for (int i = 1, l = 0, r = 0; i < n; i++){if (i <= r)a[i] = min(a[i - l], r - i + 1);while (i + a[i] < n && s[i + a[i]] == s[a[i]])++a[i];if (i + a[i] - 1 > r)l = i, r = i + a[i] - 1;}return a;
}
void solve()
{int n, kl, kr;cin >> n >> kl >> kr;string s;cin >> s;vector<int> z = z_algorithm(s);int l = 1, r = n;auto check = [&](int x){int cnt = 0;for (int i = 0; i < n; i++){if (z[i] >= x){cnt++;i = i + x - 1;}}return cnt >= kl;};int ans = 0;while (l <= r){int mid = (l + r) / 2;if (check(mid)){ans = mid;l = mid + 1;}else{r = mid - 1;}}cout << ans << endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;cin >> t;while (t--){solve();}system("pause");return 0;
}
再考虑复杂版本,我们需要求一段区间的 f f f值,我们是否还是可以利用简单版本的做法,当然是可以的,容易发现,最终的一个答案也具有单调性,即随着段数 k k k的上升,我们对应得到的答案一定是越来越小的,即 l c p lcp lcp 的长度一定会越来越小,其长度为 n k n\over k kn 。由此我们完全可以进行根号分治,当 k k k 小于某个阈值时,我们暴力的去运用简单版本的二分得到答案,当 k k k 大于该阈值时,我们就暴力的去枚举 l c p lcp lcp 的长度即可,因为最多只会枚举 n k n\over k kn次。
最终的时间复杂度为 n n l o g n + n n \sqrt nnlogn+n \sqrt n nnlogn+nn 。
#include <bits/stdc++.h>using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
typedef pair<int, int> pll;
typedef array<ll, 3> p3;
// int mod = 998244353;
const int maxv = 4e6 + 5;
// #define endl "\n"vector<int> z_algorithm(const string &s)
{int n = s.size();vector<int> a(n);a[0] = n;for (int i = 1, l = 0, r = 0; i < n; i++){if (i <= r)a[i] = min(a[i - l], r - i + 1);while (i + a[i] < n && s[i + a[i]] == s[a[i]])++a[i];if (i + a[i] - 1 > r)l = i, r = i + a[i] - 1;}return a;
}int cal(int tar,int n,vector<int> &z)//二分暴力计算
{int l = 1, r = n;auto check = [&](int x){int cnt = 0;for (int i = 0; i < n; i++){if (z[i] >= x){cnt++;i = i + x - 1;}}return cnt >= tar;};int ans = 0;while (l <= r){int mid = (l + r) / 2;if (check(mid)){ans = mid;l = mid + 1;}else{r = mid - 1;}}return ans;
}void solve()
{int n, kl, kr;cin >> n >> kl >> kr;string s;cin >> s;vector<int> z = z_algorithm(s);//计算z函数int bk=(int)sqrt(n);//阈值vector<int> f(n+5);for(int len=1;len<=bk;len++){//大于阈值,暴力枚举长度int cnt=0;for(int i=0;i<n;i++){if(z[i]>=len){i=i+len-1;cnt++;}}f[cnt]=len;}for(int i=n;i>=0;i--) f[i]=max(f[i],f[i+1]);//后缀取最大值即可,因为具有单调性for(int i=kl;i<=kr;i++){if(i<=bk){cout<<cal(i,n,z)<<" ";}else cout<<f[i]<<" ";}cout<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;cin >> t;while (t--){solve();}system("pause");return 0;
}

![[Android]四大组件简介](https://img-blog.csdnimg.cn/direct/71b3a93b94a84f6b930bc79e3279fa5c.png)