预备

符号定义

${\left(\cdot \right)}^w$表示世界坐标系下的表示，Z轴与重力方向重合。
${\left(\cdot \right)}^b$表示体坐标系下的表示，与IMU坐标系绑定。
${\left(\cdot \right)}^c$表示相机坐标系下的表示。
$q_b^w$和$p_b^w$分别表示imu 体坐标系下转换到世界坐标系下对应的旋转和平移。
$q_c^b$和$p_c^b$分别表示相机坐标系下转换到体坐标系下对应的旋转和平移。
${\left(\cdot \right)}^{b_k}$ 表示第k帧图像对应的体坐标系。
${\left(\cdot \right)}^{c_k}$ 表示第k帧图像对应的体坐标系。
$\left(\hat{\cdot }\right)$表示带误差的观测值/估计值(带噪声)。
$\bar{p}.$表示不带尺度的视觉位移估计量。

代码中常用的容器：

feature_buf存放feature_tracker_node.cpp发布的特征点信息
imu_buf存放imu_msg

measurements 中配套存放新图像帧特征点信息及其时间戳对应的IMU预积分数据。

IntegrationBase预积分结构体：
 result_delta_q/p/v指中值预积分；
 jacobian存放预积分变量的雅可比
 covariance协方差矩阵。

map<int, vector<pair<int, Eigen::Matrix<double, 7, 1>>>> image：帧特征点属性管理map
 每个特征点属性包括：(camera_id,[x,y,z,u,v,vx,vy])，索引为feature_id
 xyz_uv_velocity << x, y, z, p_u, p_v, velocity_x, velocity_y;
 image[feature_id].emplace_back(camera_id, xyz_uv_velocity);

all_image_frame存放所有图像帧数据(包含了特征点及IMU积分数据)。

f_manager存放管理特征点信息，包含各类特征点相关接口。

sfm_f统计各特征点在各帧中的观测。

pre_integrations 存放预积分量，与图像关键帧对应。

Estimator 为VIO结构体，包含各类接口及变量。

初始化原理及步骤

初始化目的

由于单目视觉的尺度信息缺失，采用IMU的位姿积分数据与通过视觉获得的位姿数据及逆行对比，从而估计出尺度信息，从而进一步得到所有特征点的坐标。
然而，完成IMU数据与相机数据的结合，需要知道相机坐标系与IMU坐标系之间的关系($q_c^b$和$p_c^b$)，而此可以通过标定数据或者带IMU相机的工厂参数获得。
通常，相机与IMU之间的角度差异带来的影响较大，而其较小的位置差异对整个里程计的位置估计影响较小，因而，其位置差异$(p_c^b)$可以被忽略。

此外，IMU数据存在零偏(零偏变化)，加速度计中包含重力加速度。

初始化原理

初始化原理核心：
通过将相机视觉得到的角度信息与IMU角度信息对比，可以估计陀螺仪零偏，以及在线估计IMU与相机之间的角度差异。

通过将相机视觉得到的位置信息于IMU加速度积分的位置信息进行对比，从而估计出尺度信息，以及修正重力加速度。

初始化步骤

 预处理：
（1） 特征点提取。IMU预积分(基于IMU的时间戳)
（2） IMU与图像时间戳对齐与关联

 关联：
（3） (若无)则估计外参

 VINS初始化:
（4） (视觉)SFM求解。
（5） 视觉惯性对齐
     陀螺仪零偏估计
     尺度，重力加速度，速度计算

初始化详细流程、原理及代码。

 预处理：
（1）特征点提取；IMU预积分。
光流法提取跟踪特征点。IMU预积分(基于IMU的时间戳)，二者分别运行于ROS两个node（feature_tracker_node.cpp和estimator_node.cpp）

1. 光流法提取跟踪特征点：feature_tracker_node.cpp
   核心函数：img_callback()：readImage()：
  createCLAHE->apply(): 首先对(太亮或太暗EQUALIZE=1)图像进行灰度直方图均衡化处理
     calcOpticalFlowPyrLK(): 使用LK光流法跟踪特征点
     outliers rejectWithF(): 通过基本矩阵剔除;
     setMask(): 设置mask保证提取特征点的均匀分布;
     goodFeaturesToTrack(): 查看是否需要提取特征点，并提取；
     undistortedPoints(): 对特征点坐标进行去畸变矫正，转换到归一化坐标系上，并计算每个角点的速度。
2. IMU预积分：estimator_node.cpp和factor/integration_base.h
imu_callback()：调用predict()发布高频PVQ，与IMU数据频率一致；
   核心函数：predict()通过中值积分计算当前时刻的PVQ,
   $${{\bar{\hat{a}}}_i}^{\prime }=\frac{1}{2}[{\hat{q}}_i({\hat{a}}_i-{\hat{b}}_{a_i})+{\hat{q}}_{i+1}({\hat{a}}_{i+1}-{\hat{b}}_{a_i})]$$$${{\bar{\hat{\omega }}}_i}^{\prime }=\frac{1}{2}({\hat{\omega }}_i+{\hat{\omega }}_{i+1})-{\hat{b}}_{\omega }$$
   
   $$\begin{array}{c}{\hat{R}}_w^{b_k}{\hat{p}}_{b_{k+1}}^w={\hat{R}}_w^{b_k}\left({\hat{p}}_{b_k}^w+{\hat{v}}_{b_k}^w\mathrm{\Delta }{t}_k-\frac{1}{2}{g}^w\mathrm{\Delta }{t}_k^2\right)+{\hat{\alpha }}_{b_{k+1}}^{b_k}\\ {\hat{R}}_w^{b_k}{\hat{v}}_{b_{k+1}}^w={\hat{R}}_w^{b_k}({\hat{v}}_{b_k}^w-g^w\mathrm{\Delta }{t}_k)+{\hat{\beta }}_{b_{k+1}}^{b_k}\\ {\hat{q}}_w^{b_k}\otimes {\hat{q}}_{b_{k+1}}^w={\hat{\gamma }}_{b_{k+1}}^{b_k}\end{array}$$
   详细参见https://blog.csdn.net/weixin_41469272/article/details/138505746

---

步骤（2）及以后都对应estimator_node.cpp的代码，核心函数process()。
imu_callback()和feature_callback()分别打包imu预积分数据及特征点数据。并通过锁机制触发process()中的操作。

estimator_node.cpp: imu_callback()/feature_callback()/process()

process()：VIO线程主函数
|–getMeasurements()： 搜集image及其时间戳附近的imu数据，打包存放到measurement。

|–estimator.processIMU()：线性插值IMU数据，使之对齐图像时间戳。
  |–new IntegrationBase
  |–IntegrationBase->push_back(): propagate(): midPointIntegration() 中值积分，得到PVQ/协方差/雅可比

|–estimator.setReloFrame()： 重定位函数。

|–estimator.processImage(): 关键帧判定；外参标定；视觉惯性对齐；初始化等
  |–f_manager.addFeatureCheckParallax(): 判断是否为关键帧，选择marg帧。
  |–f_manager.getCorresponding(): 得到两帧的共视特征点。
  |–CalibrationExRotation()：标定相机IMU外参。
    |–solveRelativeR(): 通过计算F阵解算R。

  |–initialStructure(): 初始化/初始化失败执行滑窗。
    |–relativePose(): 寻找滑窗中的枢纽帧。
    |–sfm.construct()：求解滑窗口中的所有图像帧的位姿和特征点坐标。
      |–solveFrameByPnPPnP求解帧间位姿。
      |–triangulateTwoFrames(): 三角化特征点。
    |–visualInitialAlign()初始化核心函数，通过联合视觉IMU数据，求解尺度，重力，等等。
      |–VisualIMUAlignment: 计算陀螺仪偏置，尺度，重力加速度和速度。
        |–solveGyroscopeBias(): 陀螺仪零偏估计。
        |–LinearAlignment(): 尺度，重力加速度，速度计算。
          |–RefineGravity:固定重力幅值，进一步求解重力加速度及尺度等。

  |–slideWindow(): 滑窗计算。

|–update(): 获取滑动窗口当前图像帧的imu更新项[$P,Q,V,b_a,b_{\omega },a,g$]; 更新imu_buf中的PVQ

---

|process() start-------------------------------------------------------------:

（2）IMU与图像时间戳对齐与关联

1. 打包特征点数据及其前后发布的IMU积分数据
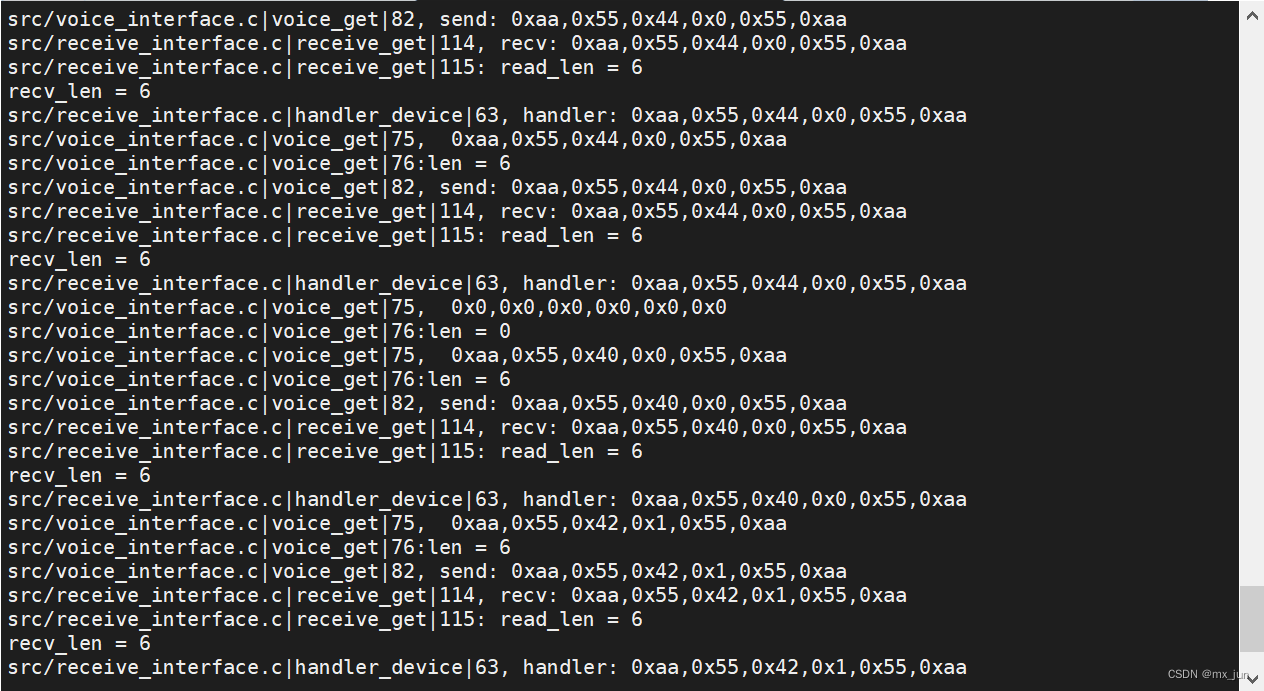
   核心函数getMeasurements()搜集image及其时间戳附近的imu数据，可出现以下两种情况:
   
   对IMU数据进行线性插值，对齐图像帧。
   将新图像帧特征点信息及其时间戳对应的IMU预积分数据配套存放在measurements 中
   measurements 中配套存放新图像帧特征点信息及其时间戳对应的IMU预积分数据。

2. IMU积分对齐图像时间戳(时间插值)
   核心函数estimator.processIMU() 计算imu数据与图像数据之间的时间差，利用中值积分及插值估算与图像帧时间戳对应的IMU积分值。
   processIMU()：new IntegrationBase对象，并通过IntegrationBase->push_back->propagate->midPointIntegration()完成与图像帧对应的中值预积分(result_delta_q/p/v)，以及预积分的雅可比(jacobian)及协方差矩阵(covariance)。

3. 创建特征点特征管理器（map）
   每个特征点属性包括：(camera_id,[x,y,z,u,v,vx,vy])s，索引为feature_id
 
map<int, vector<pair<int, Eigen::Matrix<double, 7, 1>>>> image;
   xyz_uv_velocity << x, y, z, p_u, p_v, velocity_x, velocity_y;
   image[feature_id].emplace_back(camera_id, xyz_uv_velocity);

---

以下功能均在processImage()的函数内容：关键帧判定；外参标定；初始化；VIO等
all_image_frame存放所有图像帧数据(包含了特征点及IMU积分数据)
f_manager中存放管理特征点信息，包含各类特征点相关接口
f_manager.addFeatureCheckParallax()检测视差并选择添加关键帧

---

  |processImage() start-------------------------------------------------------------:
 关联：

若需要估计外参，则估计外参$q_c^b$; 首先通过f_manager.getCorresponding()得到两帧之间的共视点。
执行核心函数CalibrationExRotation()：构建$Ax=0$问题，使用SVD方法进行求解。

原理：联合视觉帧间角度估计(solveRelativeR()通过F矩阵计算得到)与IMU角度积分值(对应图像帧)得到。
$$q_{b_{k+1}}^{b_k}\otimes q_c^b=q_c^b\otimes q_{c_{k+1}}^{c_k}$$
上式可写为
$$\left({\left[q_{b_{k+1}}^{b_k}\right]}_L-{\left[q_{c_{k+1}}^{c_k}\right]}_R\right)q_c^b=Q_{k+1}^k\cdot q_c^b=0$$
从而滑窗中的多组帧间约束，并利用鲁棒核函数构建问题：
$$\left[\begin{array}{c}{w}_1^0\cdot Q_1^0\\ w_2^1\cdot Q_2^1\\ ⋮\\ w_N^{N-1}\cdot Q_N^{N-1}\end{array}\right]q_c^b=Q_N\cdot q_c^b=0$$
其中鲁棒核函数权重：
$$w_{k+1}^k=\{\begin{array}{cc}1,& r_{k+1}^k<\delta \\ \frac{\delta }{r_{k+1}^k},& otherwise\end{array}$$
从而以上为$AX=0$的经典问题，可使用SVD方法进行求解，原理参考：https://blog.csdn.net/weixin_41469272/article/details/123696963

    |initialStructure() start---------------------------------------------------------:
 VINS初始化initialStructure()
（1）SFM求解

1. 通过计算加速度的标准差，判断是否存在足够的偏移运动，从而使得三角化更加可信；

2. 统计各特征点在各帧中的观测，存放在sfm_f中。

3. 寻找滑窗中的最后一帧有足够视差的且足够多共视点的帧作为枢纽帧，与最后一帧完成三角化及PnP。核心函数relativePose():
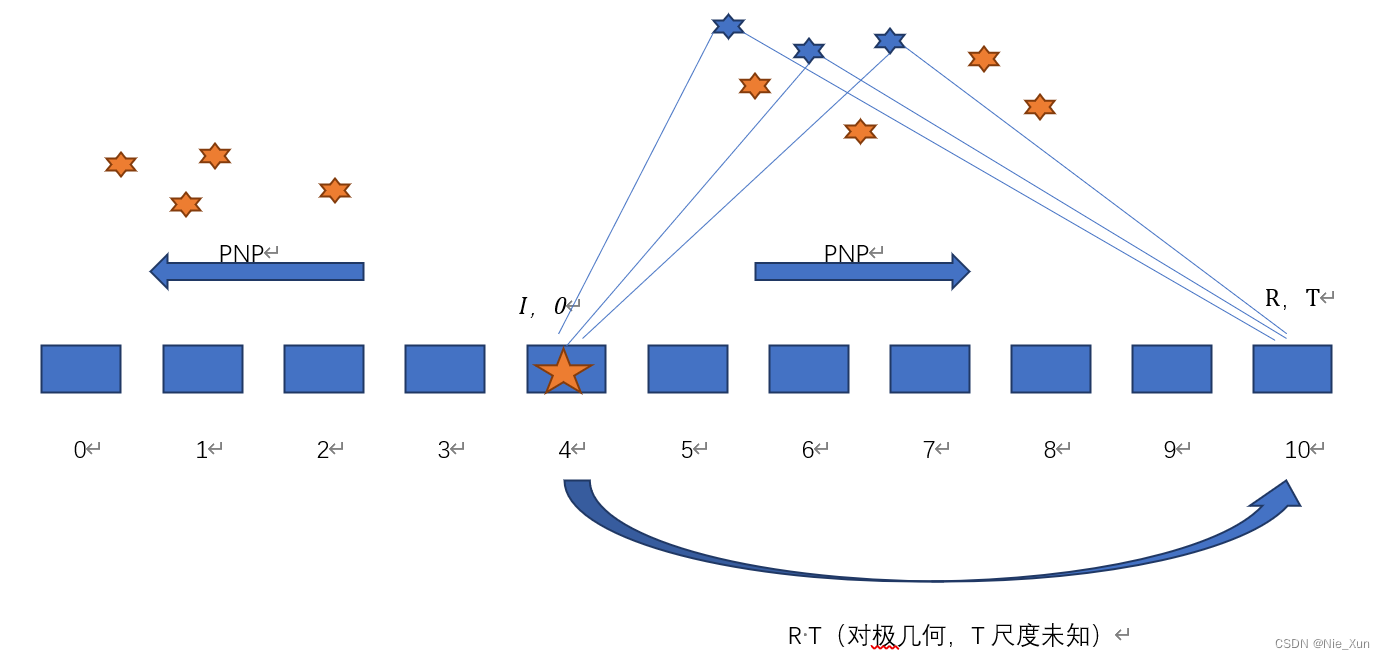   五角星指选出的枢纽帧，遍历滑窗中的帧，计算其与滑窗最后一帧之间的视差和RT，当视差足够，且计算的RT对应的内点数足够时(solveRelativeRT=true)时，则认定该帧为枢纽帧。

4. 通过上一步得到的特征点进一步使用SFM计算出滑窗中所有帧的位姿及特征点。
   核心函数sfm.construct()：求解滑窗口中的所有图像帧的位姿和特征点坐标。
    
   首先设立枢纽帧的位姿为单位阵(以枢纽帧为原点进行三角化及PNP)，叠加relativePose()的结果得到滑窗最后一帧的位姿；
    
   遍历滑窗内的帧(先从枢纽帧向后遍历，再向前遍历)，分别三角化其与滑窗中最后一帧的共视特征点(triangulateTwoFrames())，及PNP求解该帧位姿(solveFrameByPnP())；
   同时也三角化一下滑窗中相邻帧的之间的共视特征点。
   solveFrameByPnP调用cv::solvePnP函数实现；
   triangulateTwoFrames()采用构造$AX=0$，而后使用SVD方法实现三角化，原理见https://blog.csdn.net/weixin_41469272/article/details/123696963
    
   遍历所有帧(all_image_frame包括非滑窗帧)，调用cv::solvePnP函数实现得到各帧的位姿。

（2）视觉惯性对齐visualInitialAlign()
核心函数VisualIMUAlignment()
      |VisualIMUAlignment start---------------------------------------------------------：

1. 陀螺仪零偏估计solveGyroscopeBias()
   联合视觉帧间角度估计(上文SFM中得到)与IMU角度积分值(对应图像帧)得到。
   约束公式如下：
   
   $${\gamma }_{b_{k+1}}^{b_k}\approx {\hat{\gamma }}_{b_{k+1}}^{b_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{\mathbf{J}}_{b_{\omega }}^{\gamma }\delta {\mathbf{b}}_{\omega }\end{array}\right]$$
   其中:
   $${q_{b_{k+1}}^{c_0}}^{-1}\otimes q_{b_k}^{c_0}\otimes {\gamma }_{b_{k+1}}^{b_k}={q_{b_{k+1}}^{c_0}}^{-1}\otimes q_{b_k}^{c_0}\otimes {\hat{\gamma }}_{b_{k+1}}^{b_k}\otimes \left[\begin{array}{c}1\\ \frac{1}{2}{\mathbf{J}}_{b_{\omega }}^{\gamma }\delta {\mathbf{b}}_{\omega }\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]$$
   $$\left[\begin{array}{c}1\\ \frac{1}{2}{\mathbf{J}}_{b_{\omega }}^{\gamma }\delta {\mathbf{b}}_{\omega }\end{array}\right]={{\hat{\gamma }}_{b_{k+1}}^{b_k}}^{-1}\otimes {q_{b_k}^{c_0}}^{-1}\otimes q_{b_{k+1}}^{c_0}={{\hat{\gamma }}_{b_{k+1}}^{b_k}}^{-1}\otimes q_{b_{k+1}}^{b_k}$$
   只考虑虚部，从而得到AX=b的问题。
   
   其中$J_{b_w}^{\gamma }为{\gamma }_{b_{k+1}}^{b_k}$对$\delta b_w$的雅可比矩阵，作者从IntegrationBase对象的jacobian中截取。

2. 尺度，重力加速度，速度计算LinearAlignment()
   通过对比加速度积分值与相机SFM得到的偏移，计算得到尺度，重力加速度，以及速度信息
   待求解变量：
   
   约束公式如下：
   
   通过整理上式，将待求解量提取出来，可将上式化为以下形式：
   
   其中：
   
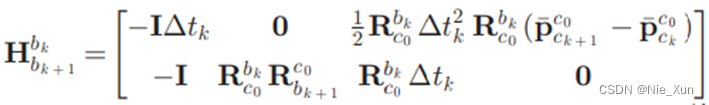
   从而可构成最小二乘问题：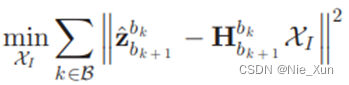
   如此问题变为$Ax=b$的问题，使用x = A.ldlt().solve(b)进行求解。
    
   RefineGravity()通过固定重力加速度幅值，从而将重力加速度变为2维参数，再次对重力加速度进行优化。
   
   图中：$\bar{\hat{g}}$表示经过上式得到的重力加速度的单位方向向量，$\left|g\right|$为指定的重力加速度的幅值，待求解$w_1,w_2$。
   此时，待优化变量变为：
   
   同时：
   
   同样的方法进行求解Ax=b问题。
   VisualIMUAlignment--------------------------------------------------end|

3. 得到重力加速度后，重新三角化及积分
   f_manager.triangulate()
pre_integrations[i]->repropagate()

4. 使用尺度信息恢复视觉偏移及特征点深度；

5. 使世界坐标系z轴对齐重力加速度方向，并将特征点转换到世界坐标系下。

…
    initialStructure--------------------------------------------------end|
…
  processImage--------------------------------------------------end|
…
process--------------------------------------------------end|

参考文献

《VINS 论文推导及代码解析 崔华坤》
《VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator》
《Quaternion kinematics for the error-state Kalman filter》