文章目录
- 题目描述
- 算法原理
- 1.状态表示(经验+题目)
- 2.状态转移方程
- 3.初始化
- 4.填表顺序
- 5.返回值
- 代码实现
- C++
- Java
题目描述
题目链接:931.下降路径最小和
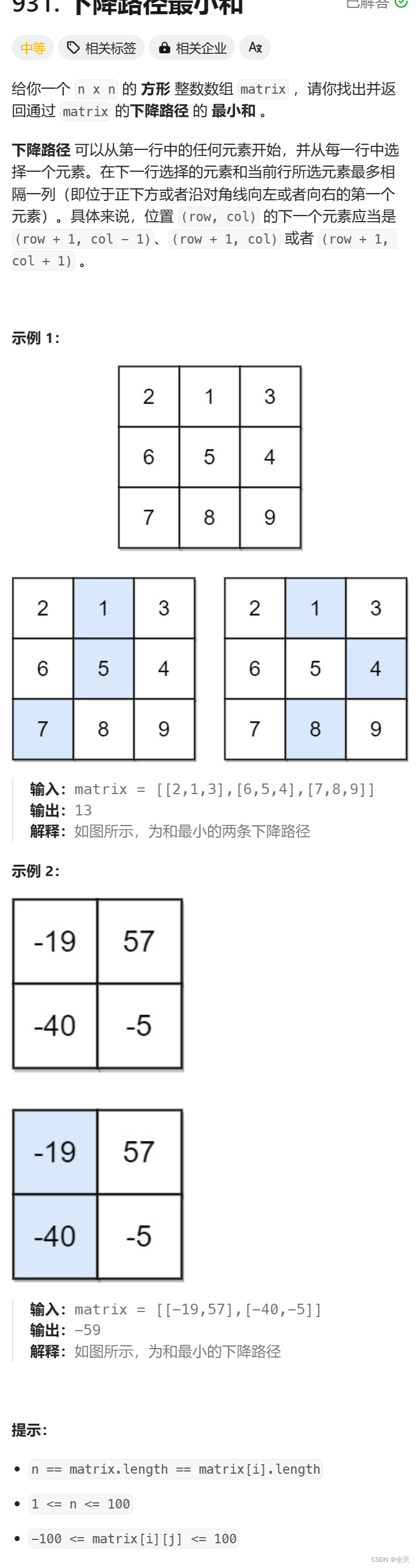
关于这⼀类题,看过我之前的博客的朋友对于状态表示以及状态转移是⽐较容易分析出来的。比较难的地方可能就是对于边界条件的处理。
算法原理
1.状态表示(经验+题目)
对于这种路径类的问题,我们的状态表示⼀般有两种形式:
- 从 [i, j] 位置出发,到达⽬标位置有多少种方式;
- 从起始位置出发,到达 [i, j] 位置,⼀共有多少种方式。
这⾥选择第⼆种定义状态表示的方式:
dp[i][j] 表示:到达 [i, j] 位置时,所有下降路径中的最小和。
2.状态转移方程
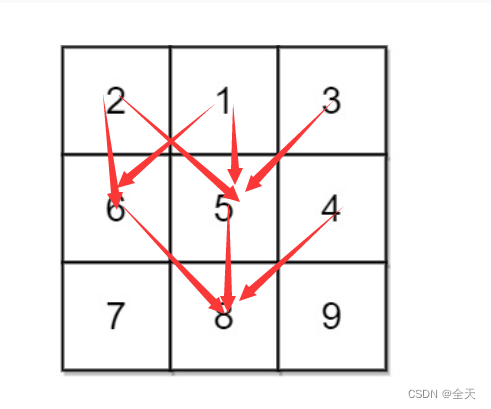
根据最近的一步划分问题。对于普遍位置 [i, j] ,根据题意得,到达 [i, j] 位置可能有三种情况:
- 从正上方 [i - 1, j] 位置转移到 [i, j] 位置;
- 从左上方 [i - 1, j - 1] 位置转移到 [i, j] 位置;
- 从右上方 [i - 1, j + 1] 位置转移到 [i, j] 位置;
我们要的是三种情况下的最小值,然后再加上矩阵在 [i, j] 位置的值。
所以得出状态转移方程:
dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j +
1])) + matrix[i - 1][j - 1]
3.初始化
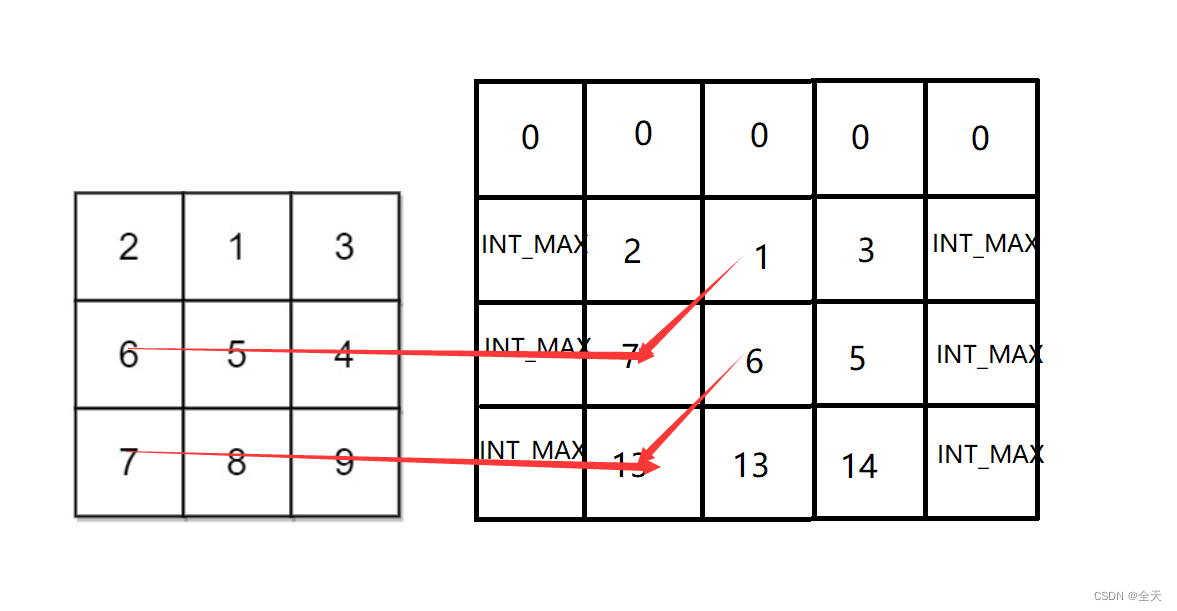
可以在最前面加上⼀个辅助结点,帮助我们初始化。使用这种技巧要注意两个点:
- 辅助结点里面的值要保证后续填表是正确的;
- 下标的映射关系。
在本题中,需要加上一行,并且加上两列。所有的位置都初始化为INT_MAX,然后将第⼀行初始化为 0 即可。
4.填表顺序
根据状态表示,填表的顺序是从上往下即可,同一行的顺序可以随意。
5.返回值
注意这⾥不是返回 dp[m][n] 的值!题⽬要求只要到达最后一行就行了,因此这⾥应该返回 dp 表中最后一行的最小值。
代码实现
C++
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {//1.创建一个dp表int n = matrix.size();vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));//2.初始化for(int k = 0;k <= n + 1;++k)dp[0][k] = 0;//3.填表for(int i = 1;i <= n;++i)for(int j = 1;j <= n;++j)dp[i][j] = min(min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + matrix[i - 1][j - 1];//这边要注意一下下标的映射关系//4.返回值int ret = INT_MAX;for(int m = 1;m <= n;++m)ret = min(ret, dp[n][m]);return ret;}
};
Java
class Solution {public int minFallingPathSum(int[][] matrix) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回结果int n = matrix.length;int[][] dp = new int[n + 1][n + 2];for (int i = 1; i <= n; i++)dp[i][0] = dp[i][n + 1] = Integer.MAX_VALUE;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i - 1][j - 1],dp[i - 1][j + 1])) + matrix[i - 1][j - 1];int ret = Integer.MAX_VALUE;for (int j = 1; j <= n; j++)ret = Math.min(ret, dp[n][j]);return ret;}
}

![[C++初阶]string的几道oj题](https://img-blog.csdnimg.cn/direct/2ec63ccb4fa34c23adeb466117060d78.png)


![【实验3.1]使用Scrapy采集豆瓣读书评分在9分以上的图书数据。 要求采集每本图书的数据,包括图书名、评分、作者、出版社和出版年份。](https://img-blog.csdnimg.cn/direct/b2b170ca58cd468faa1acbb4155242be.png)
