自适应调节Q和R的自适应UKF（AUKF_QR）的MATLAB程序-编程知识

自适应调节Q和R的自适应UKF（AUKF_QR）的MATLAB程序

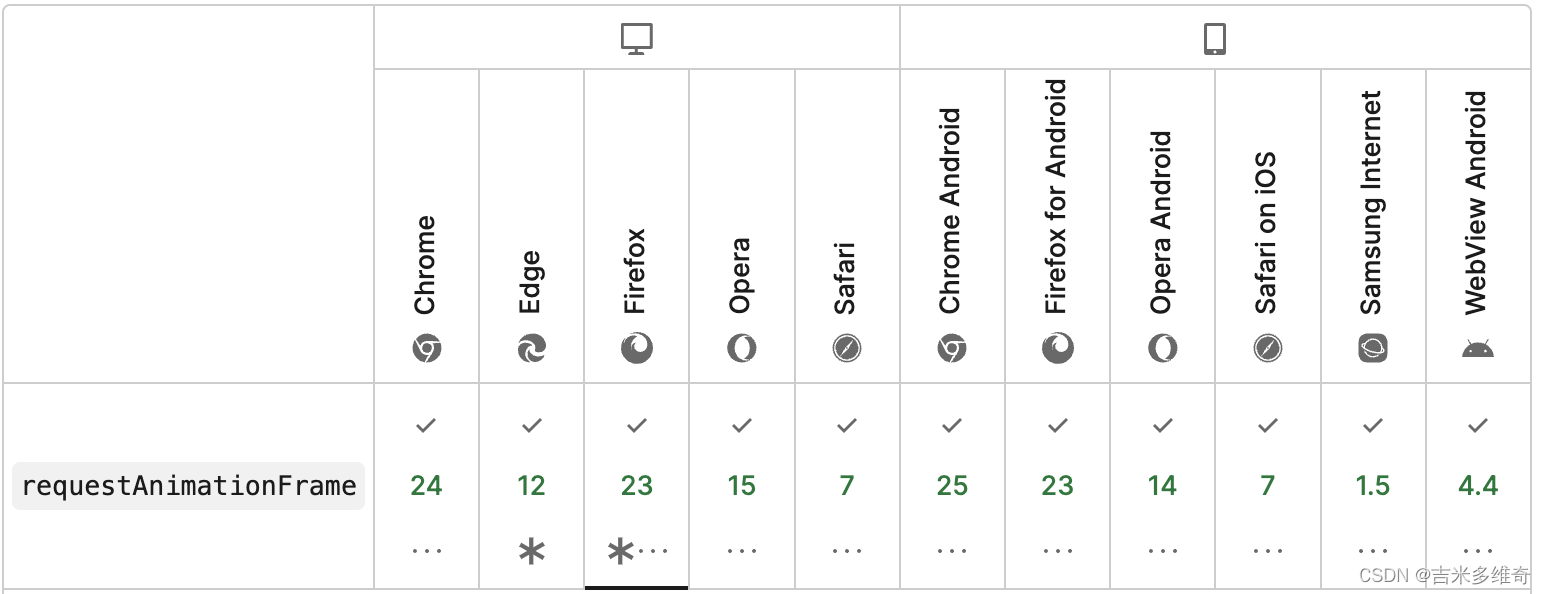
简述

基于三维模型的UKF，设计一段时间的输入状态误差较大，此时通过对比预测的状态值与观测值的残差，在相应的情况下自适应调节系统协方差Q和观测协方差R，构成自适应无迹卡尔曼滤波（AUKF），与传统的UKF相比，三轴误差的平均值得到了降低，带经典UKF的误差对比、无滤波情况下的UKF对比。带中文注释。

运行截图

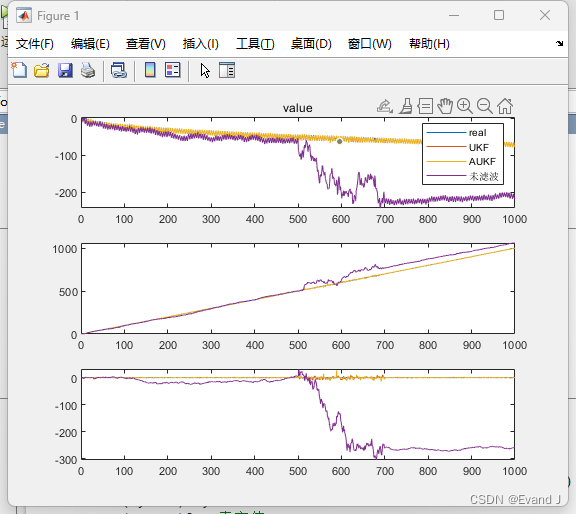
在这里插入图片描述
误差图：

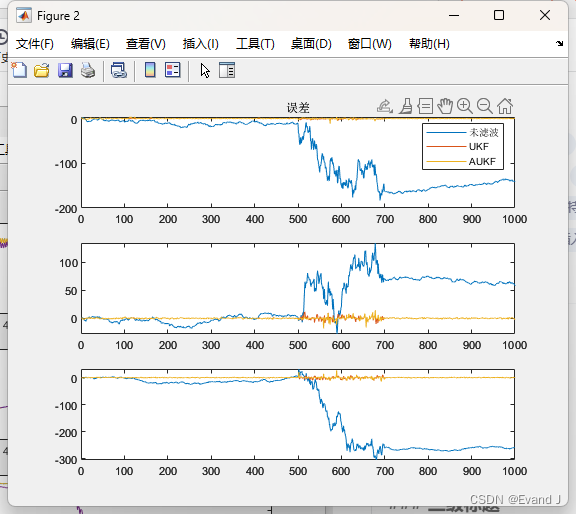
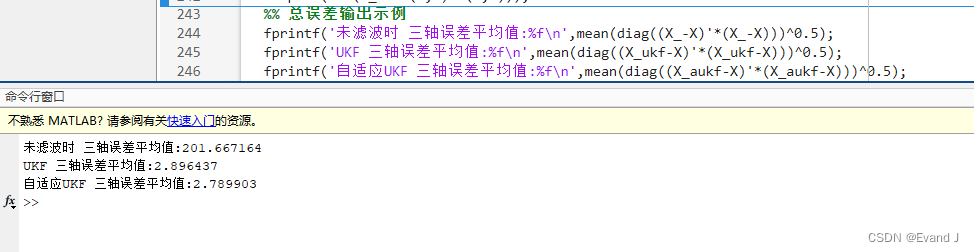
平均误差输出的结果图：

部分源代码

% 自适应调节Q和R的UKF与传统UKF效果对比
% author:Evand
% 作者联系方式：evandjiang@qq.com（除前期达成一致外，付费咨询）
% 2024-5-5/Ver1
clear;clc;close all;
%% 滤波模型初始化
t = 1:1:1000;
Q = 1*diag([1,1,1]);w=sqrt(Q)*randn(size(Q,1),length(t));
R = 1*diag([1,1,1]);v=sqrt(R)*randn(size(R,1),length(t));
P0 = 1*eye(3);
X=zeros(3,length(t));
Z=zeros(3,length(t)); %定义观测值形式
Z(:,1)=[X(1,1)^2/20;X(2,1);X(3,1)]+v(:,1); %观测量
residue_tag = 0;
%% 运动模型
X_=zeros(3,length(t));
X_(:,1)=X(:,1);
for i1 = 2:length(t)X(:,i1) = [X(1,i1-1) + (2.5 * X(1,i1-1) / (1 + X(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));X(2,i1-1)+1;X(3,i1-1)]; %真实值if i1>500 && i1<700 %设定IMU误差较大的时间段w(:,i1) = 10*w(:,i1);Z(:,i1) = [X(1,i1).^2 / 20;X(2,i1);X(3,i1)] + 10*v(i1); %观测值elsew(:,i1) = w(:,i1);endX_(:,i1) = [X_(1,i1-1) + (2.5 * X_(1,i1-1) / (1 + X_(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));X_(2,i1-1)+1;X_(3,i1-1)] + w(:,i1);%未滤波的值Z(:,i1)=[X(1,i1)^2/20;X(2,i1);X(3,i1)]+v(:,i1); %观测量
end%% UKF
P = P0;
X_ukf=zeros(3,length(t));
X_ukf(:,1)=X(:,1);
for k = 2 : length(t)Xpre = X_ukf(:,k-1);% sigma点和权重apha = 0.1; %【自己可以设置，取值：0.001~1】% calculateSigPntsandWeightsn = size(X,1);State_aug = Xpre;lambda = 3;% sigma点Sigma_Points = zeros(n, 2*n+1);Sigma_Points(:,1) = State_aug;A = chol(P,'lower');for i = 1:nSigma_Points(:,i+1) = State_aug + sqrt(lambda+n)*A(:,i);Sigma_Points(:,i+1+n) = State_aug -sqrt(lambda+n)*A(:,i);endWeights_m = zeros(2*n+1,1);for i = 1:2*n+1if i==1Weights_m(i,1) = lambda / (lambda+n);Weights_c(i,1) = lambda / (lambda+n)+1-apha^2+2;elseWeights_m(i,1) = 0.5 / (lambda+n);Weights_c(i,1) = 0.5 / (lambda+n);endend% 预测for i = 1:size(Weights_m)Sigma_pred(:,i) = [Sigma_Points(1,i)+2.5*Sigma_Points(1,i)/(1+Sigma_Points(1,i)^2)+8*cos(1.2*(k-1));Sigma_Points(2,i)+1;Sigma_Points(3,i)]+w(:,k);end% State_predXpre = Sigma_pred*Weights_m;n = size(Xpre,1);P_pred = zeros(n, n);for i = 1:size(Weights_m)x_diff = Sigma_pred(:,i) - Xpre;P_pred = P_pred + Weights_c(i,1)*x_diff*transpose(x_diff);end% 由各个状态量的点来求观测量for i = 1:size(Weights_m)Z_sigma(:,i) = [Sigma_pred(1,i)^2/20;Sigma_pred(2,i);Sigma_pred(3,i)];endZ_pred = Z_sigma*Weights_m;P_pred = P_pred+Q;X_ukf(:,k) = Xpre;% 观测更新nx = size(Xpre,1);nz = size(Z_pred,1);S = zeros(nz, nz);for i = 1:size(Weights_m)z_diff = Z_sigma(:,i) - Z_pred;S = S + Weights_c(i,1)*z_diff*transpose(z_diff);endS = S+R;TC = zeros(nx, nz);for i = 1:size(Weights_m)z_diff = Z_sigma(:,i) - Z_pred;x_diff = Sigma_pred(:,i) - Xpre;TC = TC + Weights_c(i,1)*x_diff*transpose(z_diff);endK = TC/S;% 更新P和滤波的状态量residue = Z(:,k) - Z_pred;Xpre = Xpre + K*residue;P = P_pred - K*S*transpose(K);X_ukf(:,k) = Xpre;end
%% AUKF
P = P0;
X_aukf=zeros(3,length(t));
X_aukf(:,1)=X(:,1);