x264 帧类型决策模块 x264_slicetype_decide 函数原理分析
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/687772.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
玩游戏专用远程控制软件
玩游戏专用远程控制软件:实现远程游戏的新体验
随着网络技术的不断发展和创新,远程控制软件已经逐渐渗透到我们生活的方方面面,尤其是在游戏领域。玩游戏专用远程控制软件,作为这一趋势下的产物,为玩家提供了全新的游…
全套停车场管理系统报价多少钱?停车场管理系统由哪些设备组成?
随着城市化进程的加快,汽车保有量的不断攀升,停车场的管理和运营成为城市基础设施建设的重要组成部分。一个高效、智能的停车场收费系统不仅能提升停车效率,还能增强用户体验,对城市的交通管理起到关键作用。本文将为您详细介绍全…
三下乡社会实践投稿攻略在这里
在当今信息爆炸的时代,如何让自己的声音被更多人听到,成为许多人和企业所关心的问题。其中,向各大媒体网站投稿,成为了一种常见的宣传方式。但是,如何投稿各大媒体网站?新闻媒体发文策略又有哪些呢…
论文研读 Disentangled Information Bottleneck
解耦信息瓶颈 摘要: 信息瓶颈方法是一种从源随机变量中提取与预测目标随机变量相关的信息的技术,通常通过优化平衡压缩和预测项的IB拉格朗日乘子f来实现,然而拉格朗日乘子很难优化,需要多次实验来调整拉格朗日乘子的值,…
从零开始构建现代深度学习框架:数据支持、网站链接与代码步骤
文章目录 一、数据支持二、网站链接三、代码步骤1. 导入必要的库和模块2. 加载和预处理数据(以MNIST为例)3. 定义模型结构4. 编译模型5. 训练模型6. 评估模型 一、数据支持
在构建深度学习框架的过程中,数据是不可或缺的。以下是一些可能用到…
【JavaEE网络】用Form与Ajax构建HTTP请求
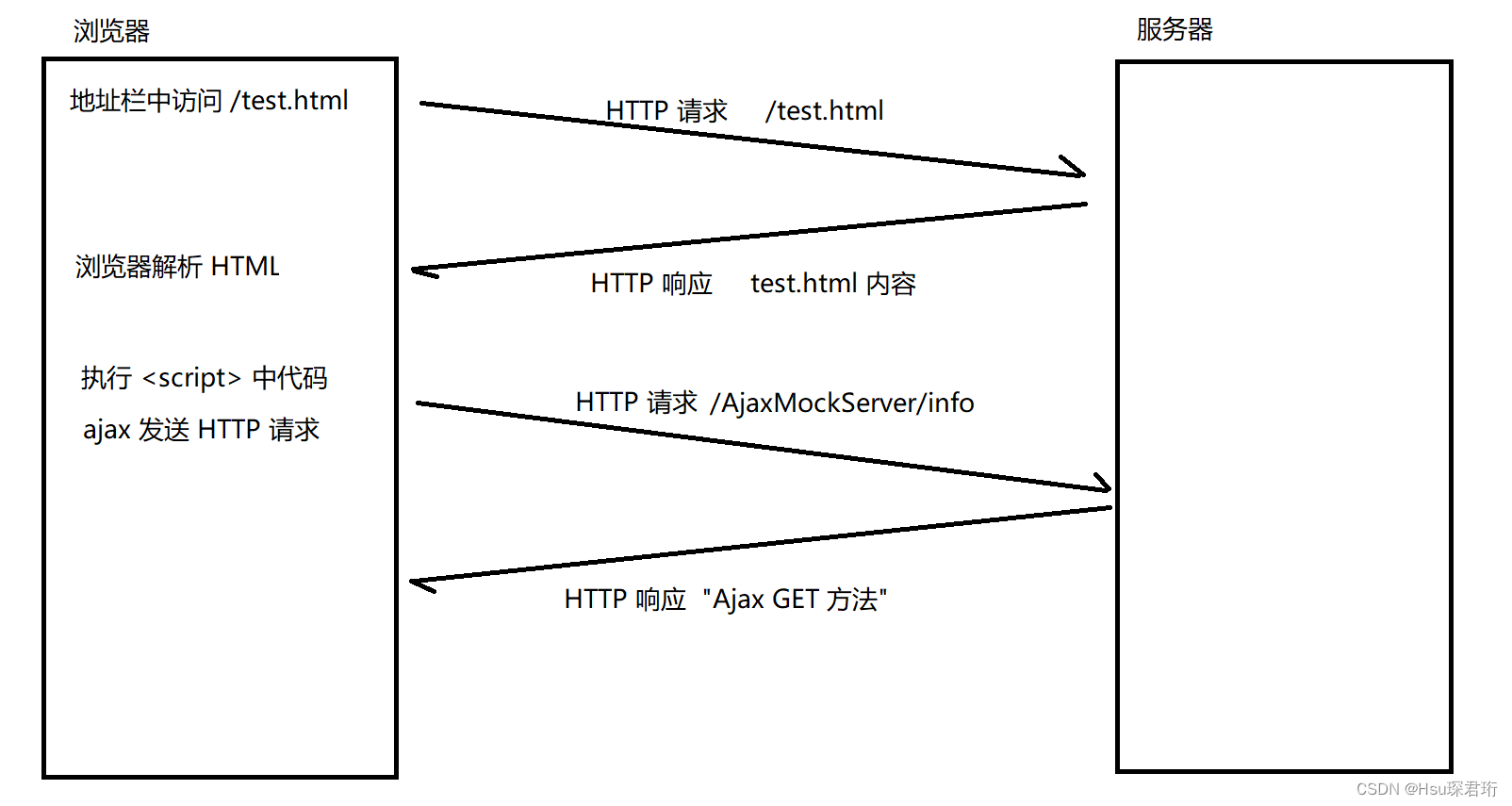
目录 通过 form 表单构造 HTTP 请求form 发送 GET 请求form 发送 POST 请求 通过 ajax 构造 HTTP 请求发送 GET 请求发送 POST 请求发送 application/json 数据封装 ajax 方法 通过 form 表单构造 HTTP 请求
form (表单) 是 HTML 中的一个常用标签. 可以用于给服务器发送 GET …
能聚合各站热点的DailyHot
什么是 DailyHot ? 今日热榜(DailyHot)是一个获取各大热门网站热门头条的聚合网站,能追踪全网热点、实现简单高效阅读。项目分为前、后端,其中后端提供了一个聚合热门数据的 API 接口。 🚩 后端 API 特性
极快响应&a…
一些Webshell-Bypass的思路
——
经过这一段时间的研究,针对webshell-Bypass我也有了一些自己的技巧,于是决定写下这篇文章,阅读前提是需要有一点PHP的语言基础。
在讲解代码之前,需要简单了解一下不同查杀平台webshell查杀的查杀原理。对于一些较传统的We…
GEE数据集——高分辨率全球树冠高度地图(1 米)Meta 公司
高分辨率 1 米全球树冠高度地图
简介
全球树冠高度地图数据集提供了对全球树冠高度的全面了解,有助于对森林生态系统、碳固存和气候变化减缓工作进行精确监测。该数据集由 Meta 和世界资源研究所合作开发,是了解森林结构和动态的基石。通过融合最先进的卫星图像和先进的人工…
Springboot+Vue项目-基于Java+MySQL的车辆管理系统(附源码+演示视频+LW)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:Java毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计 &…
下载源代码并交叉编译riscv FreeBSD系统和内核
RISCV系统曾经让人神秘到无法接触,交叉编译更是只有耳闻,现在随着RISCV的普及,它们神秘的面纱已经被慢慢揭开。
交叉编译作为RISCV系统中的一个重要环节,也随着RISCV的普及而变得更加容易理解和操作。交叉编译允许开发者在一个平…
F. Circle Perimeter
思路:线性时间复杂度就可以解决,不用二分,我们枚举横坐标,然后看当前横坐标情况下多少个纵坐标满足条件。
代码:
void solve(){int r;cin >> r;int y r, ans 0;for(int x 0;x < r;x ){ //枚举横坐标x&am…