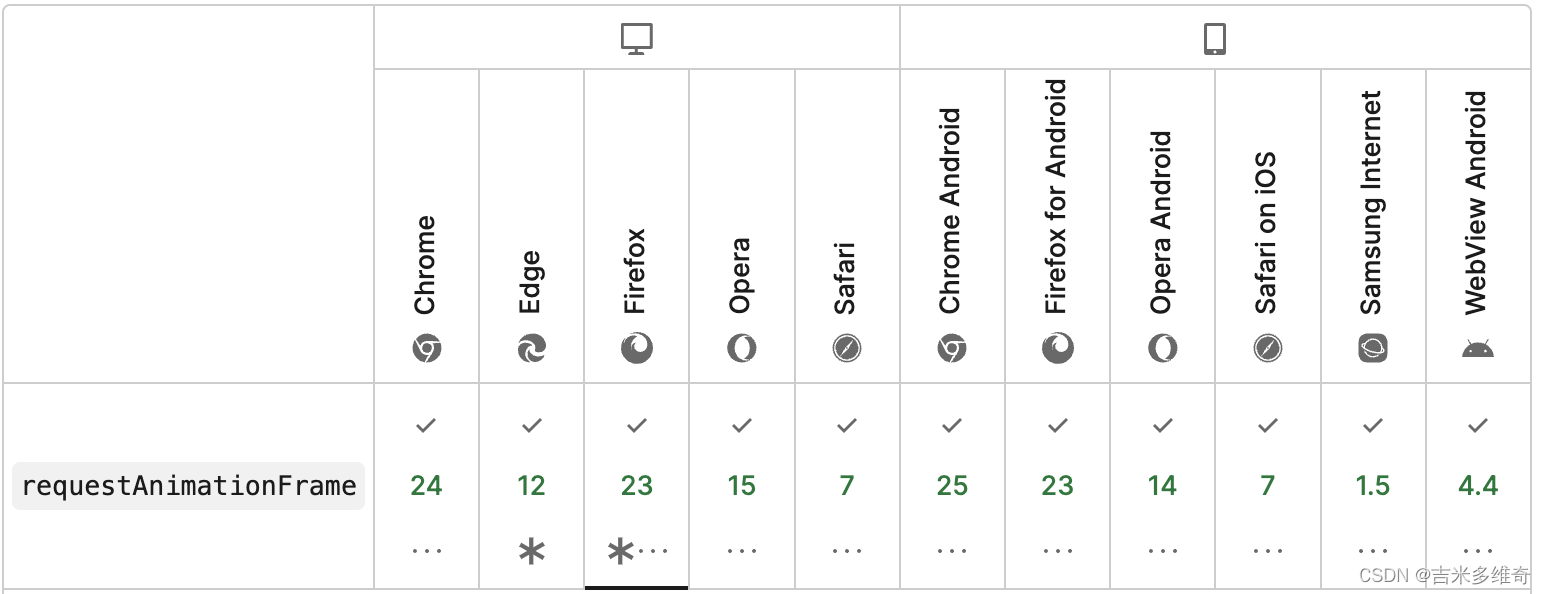
前言:今天开始学习极客时间的课程《数据结构与算法之美》。为撒要学习这个?因为做力扣题太费劲了,自己的基础太差了!所以要学习学习。开一个系列记录一下学习笔记。认真学吧,学有所获才不负韶华!之前就学过视频课《JavaScript版数据结构与算法》,稍微有了一些基础,但是还是觉得不够深入,所以又继续进行这门新课程的学习。就是不知道前端开发学习这个会不会有什么限制,且学且看吧。
一、学习的痛点
在我自己日常学习的过程中,自己总结的几个学习路上的痛点:
第一个就是学习一个东西,学着学着就容易产生一种无意义感,因为工作中基本上也用不太到。如果是工作中用到的东西,只学表层用法甚至百度都够用了,这就让自己觉得有时候深入地去看源码、学习原理,有点浪费时间,也感觉可能排不上用场。但是在我学习完 Vue的Diff算法的原理 之后,我发现真的挺神奇的,当时正好学完 diff 算法,就正好有一个 对比节点 的需求,和 Vue 中的 diff 算法的场景非常的相似,用起来也非常的契合以及快速。其实如果我没有学习 diff 算法,对于这个需求,用其他的笨方法,大概也能做出来。所以说就像这门课程的作者王争老师提到的,不管是数据结构与算法,还是其他的原理性的知识、提高性的知识,你不学,就永远觉得没用,但是你学了,总有一天你会应用上,并且比普通的笨方法更优雅。所以说,学习的过程某些意义上,就是开拓自己眼界的过程,它锻炼的不是某一个能力,而是整体思维的提升。就像健身,练腿练的不只是腿,还会锻炼到全身的力量。
然后不容易坚持的另一个原因,就是太难太枯燥🥹🥹🥹。首先要对自己拥有信心,我一定能学会!然后就是要多写,多总结,多思考,多写博客。看着自己的博客越来越多,粉丝和点赞越来越多,是一件很有成就感的事情,所以说可以让自己更加能够坚持下去。其次我觉得方法很重要,之前我刷力扣,漫无目的,基本上就随便刷,就感觉刷了也记不住,好像没啥用。后来学了 《JavaScript 版数据结构与算法》,知道了刷题最好是一个类型一个类型的刷,相似题放在一起刷,就好很多。后来跟着 《代码随想录》一起刷。但是还是觉得基础知识不足,所以继续学习。所以多向优秀的人学习,自学真的更加枯燥更加困难。
还有我觉得比较有帮助的一点就是,多看别人写的文章,这也是和别人沟通交流的一种方式。在学习的时候,多看看评论区,也是很好的交流方式。我之前学习 Monaco Editor ,就会搜一些相关的文章来看。其实大部分都写的比较浅显,没有什么原理性的东西,但是偶尔确实会发现宝藏,特别值得探索。
这个系列主要记录《数据结构与算法之美》这门课程的学习过程。但是在学习这门课程的时候,也会继续刷力扣,所以会穿插着一些自己感觉比较有用的知识点,主要来自 代码随想录
二、KMP算法
跟着代码随想录做到了 28. 找出字符串中第一个匹配项的下标 这道题,本来以为挺简单的,结果写完之后修修补补半天没做出来,看了解析发现这么复杂,涉及到我以前从来没听过的 KMP 算法。所以就来先把这个算法学一学吧。
1、名称来源
其实就是发明这个算法的三人的首字母:Knuth,Morris和Pratt
2、KMP算法解决了什么问题?
解决的就是字符串匹配的问题。
具体例子:
从 aabaabaafa 中找是否存在子串 aabaaf。
我们把 aabaabaafa 这个总的字符串叫做文本串,要找的目标子串叫做模式串。
KMP就是用来解决此类字符串匹配的问题的。
3、必知名词
- 前缀。一个字符串的前缀是包含头部字符,不包含尾部字符的所有子串
以aabaaf为例,它所有的前缀是
a
aa
aab
aaba
aabaa - 后缀。后缀和前缀相反,就是不包含头部字符,包含尾部字符的所有子串
以aabaaf为例,它所有的后缀是(从第二个字符a开始)
f
af
aaf
baaf
abaaf - 最长相等前后缀
一个字符串的最长相等前后缀,指的是先对所有的子串求得相等的前缀和后缀,然后取其中最长的结果
以aabaaf为例,咱们看一下它的子串的所有的相等前后缀
| 子串 | 相等前后缀 | 相等前后缀的长度 |
|---|---|---|
a | 没有前缀和后缀 | 0 |
aa | a | 1 |
aab | 无 | 0 |
aaba | a | 1 |
aabaa | aa | 2 |
aabaaf | 无 | 0 |
最长相等前后缀就是子串的相等前后缀中最长的,也就是 aa
- 前缀表
前缀表就是上面所有的子串的相等前后缀的长度组成的数组,就是[0, 1, 0, 1, 2, 0] - 前缀表的用法
从aabaabaafa中找是否存在子串aabaaf,肯定是需要从模式串的开头往后依次进行匹配。可以发现前面五个字符都是一样的,也就是说到f的时候匹配失败了。那么此时,不需要从头再开始匹配,因为前缀表中存储的有相等前后缀的信息。匹配失败的是f,那么就找f的前面的字符串的最长相等前后缀,就是aa。那么我们只需要从前缀aa的后面一个字符,也就是b开始,继续匹配即可,下标就是 最长相等前后缀aa的长度 2。 next数组
有些 KMP 算法中都会使用到next数组。next数组是基于 前缀表 的,原理是一样的,只是具体实现不一样,有的会将前缀表依次减1,作为next数组,有的会把前缀表整体右移作为next数组,例如上面的前缀表,右移之后就变成了[-1, 0, 1, 0, 1, 2, 0]但是原理都是一样的,只是实现上不一样。直接将前缀表作为next数组也没毛病。
4、构造 next 数组
上面我们已经讲过,aabaaf 的前缀表是 [0, 1, 0, 1, 2, 0]。关于 next 数组的构造,这里就使用前缀表作为 next 数组。这一小节来实现以下构造 next 数组的方法 getNext()。
① 初始化
getNext() 接收的参数分别是 next 数组和目标字符串。
next 数组记录的是相等先后缀的长度,那么我们首先需要两个指针,一个 i 指向后缀的末尾位置;一个 j 指向前缀的末尾位置
由于 i 指向后缀的末尾位置,其实就是 for 循环中的循环变量的作用,所以 i 不用在额外的考虑它的初始化。而 当 i = 0 的时候,j 肯定也是0,所以j初始化为0。
function getNext(str) {let next = [];let j = 0;next[0] = j;for (let i = 0; i < str.length; i++) {}
}
② 处理前后缀相同的情况
假设此时的已经遍历到了 aaba ,此时的 i 指向的是 尾部的 a,j 指向的是 头部的 a ,此时头尾相同,那么 j 就需要往前移动,去找 aa 能不能作为相等前后缀,此时的 j 是1,push到 next 数组中。
function getNext(str) {let next = [];let j = 0;next[0] = j;for (let i = 0; i < str.length; i++) {// 如果 i 和 j 指向的数值相等if(str[i] == str[j]){j++;}}
}
③ 处理前后缀不相同的情况
接着上面的 aabaa,此时 j = 2,下一次,字符串就会变成 aabaaf,i 就会 指向 f,j 指向 b,此时已经不能相等了,那么就要回退 j ,此时要回退到 next[j-1] 的位置。这就是应用前缀表。但是!回退不能只进行一步,因为回退完,可能还不相等,所以要使用 while 进行回退
function getNext(str) {let next = [];let j = 0;next[0] = j;for (let i = 0; i < str.length; i++) {while (j > 0 && str[i] != str[j]) {j = next[j - 1]}// 如果 i 和 j 指向的数值相等if (str[i] == str[j]) {j++;}next[i] = j}
}
为什么要先处理不相等的情况?因为回退完可能找到了!
相关力扣试题:28. 找出字符串中第一个匹配项的下标
三、复杂度分析
每次做算法题,分析时间复杂度和空间复杂度都有那么七八分是靠猜测。那么今天就细致的研究总结一下,究竟怎么清晰地分析复杂度。
数据结构与算法,解决的就是代码运算过程中的 “快” 和 “省” 的问题,我们不断地优化算法,就是为了让代码运行的时间更短,更加节省空间。那么就需要一个标准去衡量我们的算法是不是真的更快、更省。所以复杂度这个概念应运而生。
(一)代码执行时间
我们需要通过分析代码知道代码的执行时间。当然我们不可能知道真实的执行时间,因为没有运行环境、网络环境等。但是我们可以知道相对的执行时间。对于 cpu 来说,执行一行代码所需的时间基本是相等的。那么我们可以假设这个事件为 unitTime。那么看一下下面这段代码
int cal(int n) {int sum = 0; // 1int i = 1; // 1for (; i <= n; ++i) {sum = sum + i;} // 2nreturn sum;
}
这个方法,前两行都是 1 * unitTime,for 循环要执行 n 次,并且还有一个 ++i 的隐藏行,所以需要的时间是 2n * unitTime ,那么总共需要的时间为 (2 + 2n) * unitTime
根据这个逻辑,再看一下复杂一点的代码
int cal(int n) {int sum = 0;int i = 1;int j = 1;for (; i <= n; ++i) {j = 1;for (; j <= n; ++j) {sum = sum + i * j;}}
}
前三行都是 1 * unitTime,外层 for 循环 是 2n * unitTime,内层 for 循环 是 n * 2n * unitTime
总共就是 (3 + 2n + 2n^2) * unitTime
虽然说我们没有办法获取真实的代码执行时间,但是可以知道一个规律:代码执行时间和每行代码的执行次数总和成正比。
我们用 T(n) 表示代码执行时间,用 f(n)表示每行代码的执行次数,引入 O 表示法,可以得到
T(n) = O(f(n))
n 表示数据规模,O 就表示代码执行时间和代码执行的总次数之间的正比关系,
那么第一个例子中的代码执行时间就可以表示为 T(n) = O(2 + 2n) ;第二个例子中的代码执行时间就可以表示为 T(n) = O(3 + 2n + 2n^2)
O 表示代码执行时间随着数据规模增长的变化趋势,所以,也叫作渐进时间复杂度,简称 时间复杂度
当 n 很大的时候,公式中的低阶、常量、系数三部分对代码执行时间的增长趋势影响不大,所以可以忽略。
那么,第一个例子的时间复杂度可以写作 T(n) = O(n) ,第二个时间复杂度可以写做 T(n) = O(n^2)
(二)时间复杂度分析
关于分析时间复杂度,这里有分析法则
- 只关注循环次数最多的一段代码
时间复杂度表示的只是一种变化趋势,在分析的时候,会忽略低阶、常量、系数这三部分内容,所以我们只需要关注循环次数最多的一段代码就可以了,拿上面的例子
int cal(int n) {int sum = 0;int i = 1;for (; i <= n; ++i) {sum = sum + i;}return sum;}
常量级别的执行过程可以忽略,只需要看 for 循环的执行次数为 O(2n),然后再忽略系数就是 O(n)
- 加法法则:总的时间复杂度等于量级最大的那段代码的复杂度
还是找一段示例代码
int cal(int n) {int sum_1 = 0;int p = 1;for (; p < 100; ++p) {sum_1 = sum_1 + p;}int sum_2 = 0;int q = 1;for (; q < n; ++q) {sum_2 = sum_2 + q;}int sum_3 = 0;int i = 1;int j = 1;for (; i <= n; ++i) {j = 1; for (; j <= n; ++j) {sum_3 = sum_3 + i * j;}}return sum_1 + sum_2 + sum_3;}
一行一行的常量级代码就可以直接忽略不看
第一个 for 循环,执行的是100 次,但是它也是一个有大小的常量,所以也忽略
第二个 for 循环,时间复杂度是 O(n)
第三个 for 循环,时间复杂度是 O(n^2)
低阶的时间复杂度也可以忽略,所以这段代码的时间复杂度是 O(n^2)
所以可以得出结论,两个时间复杂度相加的结果就等于那个更大的时间复杂度。作者大大的公式:
如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n))).
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
其实这个法则在上边的代码分析的过程中已经用到了
int cal(int n) {int sum = 0;int i = 1;int j = 1;for (; i <= n; ++i) {j = 1;for (; j <= n; ++j) {sum = sum + i * j;}}
}
for 循环嵌套得到的时间复杂度就是外层的执行次数 O(n) 乘以内层的 O(2n) ,结果就是 O(n^2)
也就是说,两个时间复杂度相乘的结果,其实就是将O里面的公式相乘
类比加法法则的公式,可以得出乘法法测的公式如下:
如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n)).
(三)几种常见的时间复杂度分析
总结常见的时间复杂度,按照量级从小到大排列

上面的时间复杂度量级可以分为两类:多项式量级和非多项式量级。飞多项式量级是两个画波浪线的指数阶和阶乘阶,它们的时间复杂度非常高,这类算法问题叫做NP(Non-Deterministic Polynomial,非确定多项式)问题,通常可用性都比较差,因为执行时间随着数据规模的增长,会快速的变得很长,因此尽量不要使用这种算法。
其他的多项式量级的算法是我们可以经常使用的。
🧞♀️ O(1)
常量级时间复杂度,只要代码执行时间不随数据规模的增大而增大,时间复杂度都是 O(1)。例如下面的代码:
int i = 8;
int j = 6;
int sum = i + j;
一般来说,只要没有循环、递归,即便代码再长,时间复杂度也是 O(1)
🧞♀️ O(logn)、O(nlogn)
对数阶时间复杂度是比较常见的一种时间复杂度,也是比较难分析的一种。
以下面的代码为例:
i=1;
while (i <= n) {i = i * 2;
}
这段代码的时间复杂度怎么算呢?其实就是循环里面的代码执行的次数。循环结束的条件是 2^x = n,那么 x = log2(n) 以2为底的对数。
即时间复杂度就是 O(log2(n))
那么再分析下面一段代码
i=1;
while (i <= n) {i = i * 3;
}
它的时间复杂度其实就是 O(log3(n)) 以3为底的对数
不管底数是多少,只要是对数级别,统统将其记为 O(logn),也就是以 10 为底的对数
因为对数之间是可以这样转化的:
log3(n) 就等于 log3(2) * log2(n),所以 O(log3(n)) = O(C * log2(n)),其中 C 是一个常量,在计算时间复杂度的时候可以忽略。所以,O(log3(n)) = O(log2(n))。因此对数级时间复杂度我们可以直接忽略底数,记作 O(logn)
对于 O(nlogn) 而言,根据之前讲到的乘法法则,代码循环 n 次,时间复杂度就乘以 n,那么对数级的运算执行 n 次的情况下,时间复杂度就是 O(nlogn)
🧞♀️ O(m+n)、O(m*n)
这两种时间复杂度由两个数据规模决定,由于无法确定两个数据规模的大小,所以都不能直接忽略
第一种代码示例
int cal(int m, int n) {int sum_1 = 0;int i = 1;for (; i < m; ++i) {sum_1 = sum_1 + i;}int sum_2 = 0;int j = 1;for (; j < n; ++j) {sum_2 = sum_2 + j;}return sum_1 + sum_2;
}
两次循环分别是 m 次和 n 次,时间复杂度为 O(m+n)
第二种
int cal(int m, int n) {int sum_1 = 0;int i = 1;int sum_2 = 0;int j = 1;for (; i < m; ++i) {sum_1 = sum_1 + i;for (; j < n; ++j) {sum_2 = sum_2 + j;}}return sum_1 + sum_2;
}
嵌套循环,时间复杂度为 O(m*n)
(四)空间复杂度
时间复杂度的全称是渐进时间复杂度,表示代码执行时间和数据规模之间的增长关系。与之类似的,空间复杂度全称为渐进空间复杂度,表示的是算法的存储空间与数据规模之间的增长关系。来看一下一段简单的示例代码
void print(int n) {int i = 0; // 常量级int[] a = new int[n];for (i; i <n; ++i) {a[i] = i * i;}for (i = n-1; i >= 0; --i) {print out a[i]}
}
和时间复杂度类似,空间复杂度中的常量级、低阶、系数可以忽略,上述示例的空间复杂度由第三行代码决定,创建了一个长度为 n 的数组,即整段代码的空间复杂度为 O(n)
和时间复杂度相比,空间复杂度的分析很简单。常见的空间复杂度就是 O(1)、O(n)、O(n^2 ),其他的并不多见,不需要花费太多时间学习。
(五)四种时间复杂度分析
通过上面的学习我们掌握的基本的时间复杂度的算法,这一小节我们再来稍微拓展一丢丢,学习四种时间复杂度的分析:
最好情况时间复杂度(best case time complexity)
最坏情况时间复杂度(worst case time complexity)
平均情况时间复杂度(average case time complexity)
均摊时间复杂度
先看一下示例代码
// n表示数组array的长度
// n表示数组array的长度
int find(int[] array, int n, int x) {int i = 0;int pos = -1;for (; i < n; ++i) {if (array[i] == x) {pos = i;break;}}return pos;
}
这段代码是在数组中寻找 x,如果能找到 x 就停止循环,返回 x 的位置。
- 最好情况时间复杂度、最坏情况时间复杂度
那么这段代码的时间复杂度怎么求呢?如果在第一个索引为 0 的位置就找到了 x,那么循环中的代码只需要执行一次;如果在最后的位置才找到 x 或者没有找到 x,循环中的代码就需要执行 n 次。对于这种情况,我们就需要使用最好情况时间复杂度和最坏情况时间复杂度。最好情况时间复杂度是在最理想情况下的时间复杂度,在这段代码中就是 O(1);最坏情况时间复杂度就是最糟糕的情况下的时间复杂度,在这段代码中就是 O(n)。
- 平均情况时间复杂度
上面的最好的情况和最糟糕的情况其实都不多见,我们还需要分析一下平均情况时间复杂度
首先,x 可能在数组中,也可能不在数组中,这两种情况,虽然概率不一样,但是可以简化一下,认为各占二分之一。另外,对于在数组中的情况,可能在 0 ~ n-1 位置的概率,都是 1/n,那么占总体的概率的 1/(2n)。时间复杂度就应该是出现在某位置的概率 * 出现在某位置处需要执行的次数,就是
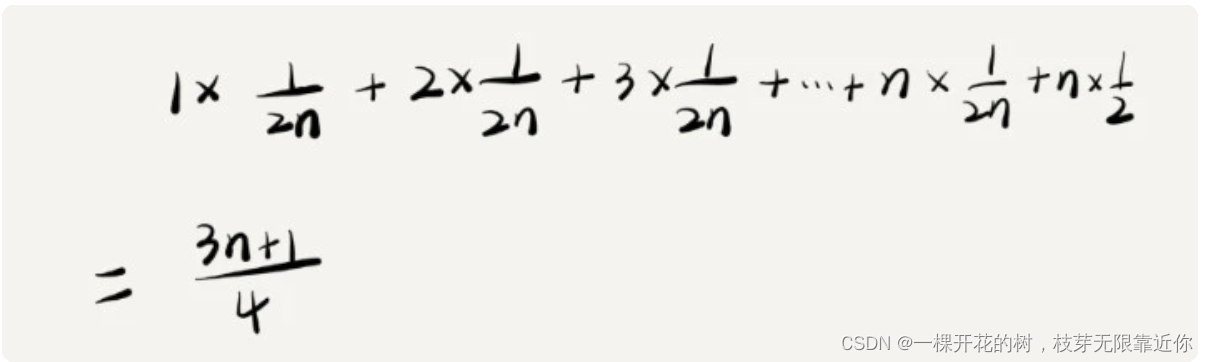
这个值在概率论中叫做加权平均值,也叫做期望值;平均情况时间复杂度也叫做加权时间复杂度,或者期望时间复杂度
忽略系数和常量,平均情况时间复杂度就是 O(n)
- 均摊时间复杂度
下面再学习一个更加高级的概念–均摊时间复杂度
均摊时间复杂度和平均情况时间复杂度比较容易弄混,它的应用场景比较有限,简单的了解一下。
看一下下面的示例代码
// array表示一个长度为n的数组// 代码中的array.length就等于n
int[] array = new int[n];
int count = 0;void insert(int val) {if (count == array.length) {int sum = 0;for (int i = 0; i < array.length; ++i) {sum = sum + array[i];}array[0] = sum;count = 1;}array[count] = val;++count;
}
上述代码实现了往数组中插入元素的功能,数组的长度为 n,调用 insert() 往数组中插入元素,count 表示实际插入了多少个元素,如果当前数组没有满, 就直接插入到 count 的位置;如果数组长度大于等于 n ,就将数组元素求和,放在第一个位置,再插入元素。
那么这段代码的时间复杂度是多少呢?我们分别分析一下,上面讲到的三种时间复杂度。
首先如果数组没有满,只需要把元素插入到 count 的位置,最好情况时间复杂度为 O(1);如果数组已经满了,那么就需要遍历数组求和,循环中的代码执行的次数为 n,最坏情况时间复杂度为 O(n);
平均时间复杂度的分析稍微复杂一些。
首先大的情况分为两种,一种是数组没满,count 可能是 0 ~ n-1 任意一个数字,共有 n 种情况;另外一种是数组满了,count 就等于 n + 1;当数组没满时时间复杂度都是 O(1),数组已经满时时间复杂度是 O(n),因此平均情况时间复杂度的计算如下
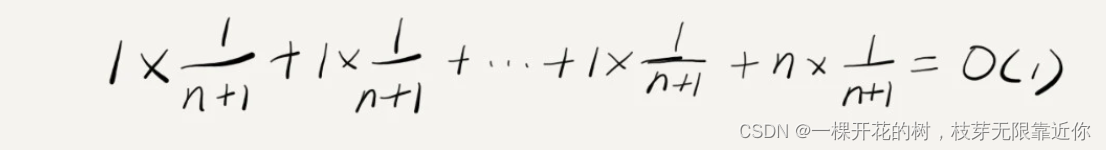
对于这个例子来说,时间复杂度的计算有一些特殊的地方,首先就是绝大部分时候的时间复杂度都是 O(1),只有个别情况时间复杂度是 O(n);另外时间复杂度的出现是一个循环过程,先是 n 次的 O(1),然后是一次 O(n),然后又是 n-1 次的O(1)……如此这般循环往复
针对这种特殊的场景,我们引入了一种特殊的分析方法:摊还分析法;通过摊还分析得到的时间复杂度我们称之为 均摊时间复杂度
每一次 O(n)的操作后面都跟随着 n-1 次的 O(1) 操作。所以把耗时多的操作,均摊到耗时少的 O(1) 操作上,均摊下来,这一组连续操作的均摊时间复杂度就是 O(1)
均摊时间复杂度的应用场景比较少,只需要稍微理解一下这个概念就行。简单总结一下它的应用场景:
对一组数据结构进行连续操作时,大部分情况下时间复杂度都很低,只有个别情况时间复杂度比较高,并且在高时间复杂度后面,跟着连续的低时间复杂度的操作,此时就可以将一组操作放到一块儿进行分析,将高时间复杂度平均到低时间复杂度上,能够使用均摊分析的场景中,一般均摊时间复杂度就等于最好情况时间复杂度。
![[蓝桥杯]真题讲解:AB路线(BFS+分层图)](https://img-blog.csdnimg.cn/direct/75f3e9de755a4956bc72cb08e1bdb3e6.png)


![[Bug]:由于中国防火墙,无法连接 huggingface.co](https://img-blog.csdnimg.cn/direct/acd03f89821d49a49fd6e95843385919.jpeg)