完全背包理论基础

​ 完全背包和0-1背包的最大区别在于完全背包里的每个物品的数量都是无限个，而0-1背包每个物品只有一个；

内嵌循环遍历顺序

​ 回顾一维数组0-1背包的遍历递推公式：

	for (int i = 0； i < weight.size(); i++) {for (int j = bagSize; j >= weight[i]; j--) {dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}

​ dp[i][j]是由dp[i - 1][j]以及dp[i - 1][j - weight[i]] + value[i]推导出来的，所有状态都依赖于上一层的状态,

​ 当二维数组压缩为一维数组，失去了i维度的辅助，根据递推公式，此时dp[j]只和左边的以及自己本身有关；

​ 如果正序遍历，由于依赖上一时刻状态，此时前面的数值已经被更新为了当前时刻的状态，后续值会出错；

​ 因此从右向左递推可以保证后面的数据还是基于未被修改的数据计算得到的，因此必须倒序遍历；

​ 所以内嵌循环选择倒序遍历可以确保每个数只添加一次；

​

​ 而完全背包由于没有这种物品数量的限制，那么完全背包就可以正序遍历：

	for (int i = 0; i < weight.size(); i++) {for (int j = weight[i]; j <= bagSize; j++) {dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}

​ 此处完全背包严格意义上来说，对应的递推公式应该是：

	dp[i][j] = max(dp[i - k][j], dp[i][j - k * weight[i]] + k * value[i])//其中，k是取值范围从0到j/weight[i]的整数(闭区间)，表示对于第i个物品，在for循环的过程中其实已经实现了取不同k的这个功能

​ dp[j]更新用的值全都是基于本行的左侧的元素进行更新，所以完全背包能也只能正序遍历；

​ 如果采用倒序遍历，那么在内层循环中对状态的更新将会影响后续更小容量背包的状态计算，从而导致错误的解。

遍历背包和物品的先后顺序

​ 对于01背包：

​ 二维dp数组的两个for遍历的先后循序是可以颠倒的；

​ 一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量；

​ 对于纯完全背包：

​ 因为dp[j] 是根据下标j之前所对应的dp[j]计算出来的；

​ 只要保证下标j之前的dp[j]都是经过计算的就可以了，颠倒是不会影响结果的；

​ 以下例说明：

​ 背包最大重量为4。

​ 物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

​ 遍历物品在外层循环，遍历背包容量在内层循环，状态如图：

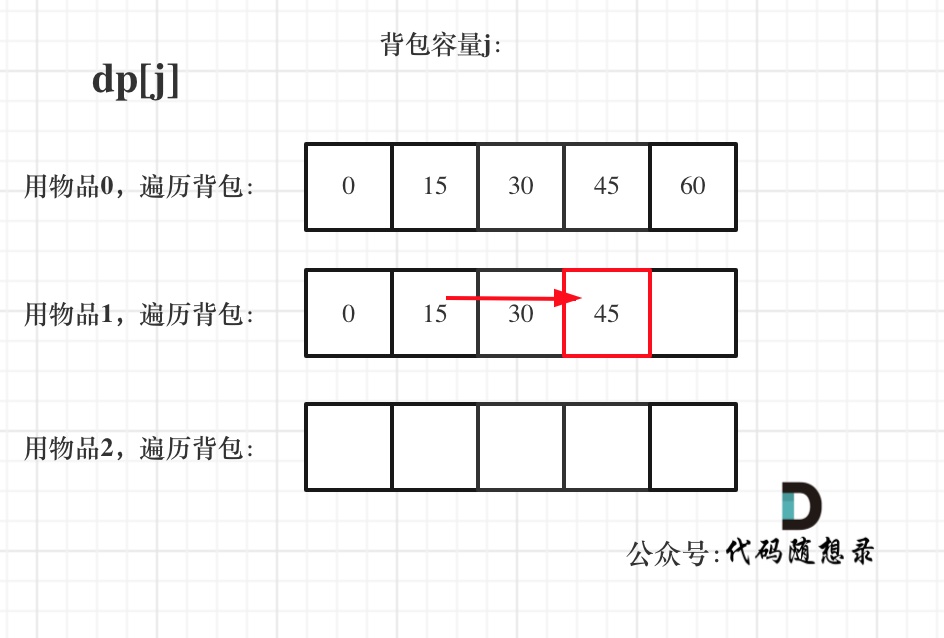
遍历背包容量在外层循环，遍历物品在内层循环，状态如图：

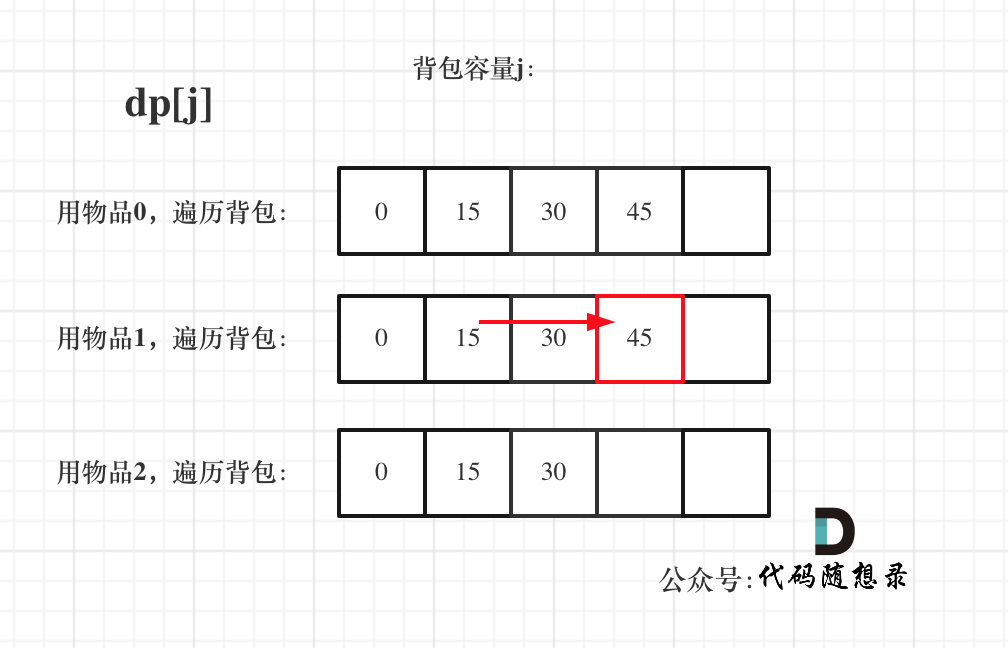
int completePack(vector<int>& weight, vector<int>& value, int bagweight) {vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}return dp[bagWeight];
}

零钱兑换Ⅱ

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

示例 1:

• 输入: amount = 5, coins = [1, 2, 5]
• 输出: 4

解释: 有四种方式可以凑成总金额:

• 5=5
• 5=2+2+1
• 5=2+1+1+1
• 5=1+1+1+1+1

示例 2:

• 输入: amount = 3, coins = [2]
• 输出: 0
• 解释: 只用面额2的硬币不能凑成总金额3。

示例 3:

• 输入: amount = 10, coins = [10]
• 输出: 1

注意，你可以假设：

• 0 <= amount (总金额) <= 5000
• 1 <= coin (硬币面额) <= 5000
• 硬币种类不超过 500 种
• 结果符合 32 位符号整数

​ 若将本体视为一个背包问题，则amount就是背包的容量，coins[i]既是weight[i]又是value[i];

​ 由于硬币可以重复选取，既可以视为完全背包问题；

​ 动规五部曲：
​ 1.确定dp数组下标及其含义：
​ dp[j]表示总金额为j时有dp[j]种方式可以凑成；

​ 2.dp数组递推公式：
​ dp[j] += dp[j - coins[i]];

​ 这里的递推公式和494.目标和的递推公式是一样的；

​ 3.初始化：

​ dp[0] = 1;这里的dp[0] = 1严格意义来说是解释不通的，但是由于递推公式的存在，所以只能取dp[0] = 1;

​ 4.遍历顺序：

​ 注意此题要求求的是组合数，下面写出两种遍历方式：

	for (int i = 0; i < coins.size(); i++) {for (int j =0; j <= amount; j++) {//以[1,2]为例//先放coins[0] = 1进去遍历，再放coins[1] = 2进去遍历//所以只会出现集合{1，2}，不会出现{2，1}//即此时出现的是组合数}}for (int j = 0; j <= amount; j++) {for (int i =0; i < coins.size(); i++) {//以[1,2,5]为例//遍历背包，则每一个容量下都会遍历所有的元素//即既会出现{1，2},也会出现{2，1}//即此时出现的是排列数}}

​ 5.打印数组：

​

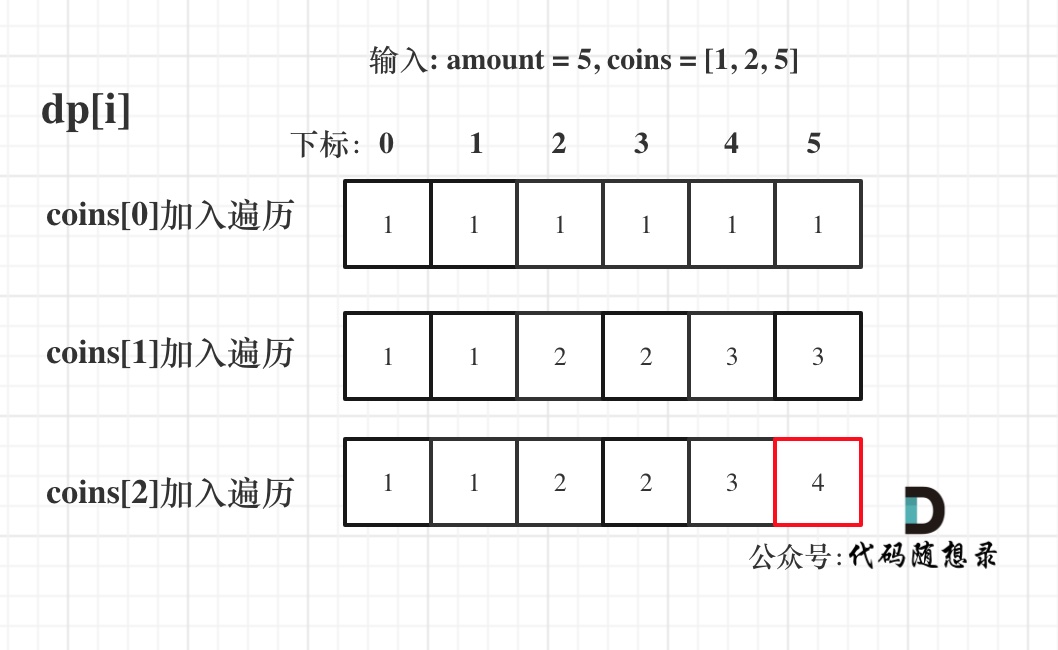
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);dp[0] = 1;for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包dp[j] += dp[j - coins[i]];}}return dp[amount];}
};

组合总和Ⅳ

给定一个由正整数组成且不存在重复数字的数组，找出和为给定目标正整数的组合的个数。

示例:

• nums = [1, 2, 3]
• target = 4

所有可能的组合为： (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)

请注意，顺序不同的序列被视作不同的组合。

因此输出为 7。

​ 和上题一样的思路，只是这里{1，3}和{3，1}视为两个组合，改变遍历顺序即可；

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target + 1, 0);dp[0] = 1;for(int j = 0; j <= target; j++){for(int i = 0; i < nums.size(); i++){if (j - nums[i] >= 0 && dp[j] < INT_MAX - dp[j - nums[i]]) {//避免相加超过int型dp[j] += dp[j - nums[i]]; }   }}return dp[target];}
};