目录
- 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
- 第二周:优化算法 (Optimization algorithms)
- 2.1 Mini-batch 梯度下降(Mini-batch gradient descent)
- 2.2 理解 mini-batch 梯度下降法(Understanding mini-batch gradient descent)
第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
第二周:优化算法 (Optimization algorithms)
2.1 Mini-batch 梯度下降(Mini-batch gradient descent)
本周将学习优化算法,这能让你的神经网络运行得更快。机器学习的应用是一个高度依赖经验的过程,伴随着大量迭代的过程,你需要训练诸多模型,才能找到合适的那一个,所以,优化算法能够帮助你快速训练模型。
其中一个难点在于,深度学习没有在大数据领域发挥最大的效果,我们可以利用一个巨大的数据集来训练神经网络,而在巨大的数据集基础上进行训练速度很慢。因此,你会发现,使用快速的优化算法,使用好用的优化算法能够大大提高你和团队的效率,那么,我们首先来谈谈 mini-batch 梯度下降法。

你之前学过,向量化能够让你有效地对所有𝑚个样本进行计算,允许你处理整个训练集,而无需某个明确的公式。
所以我们要把训练样本放大巨大的矩阵𝑋当中去,𝑋 = [ x ( 1 ) x ( 2 ) x ( 3 ) … … x ( m ) ) x^{(1)} x^{(2)} x^{(3)} … … x^{(m)}) x(1)x(2)x(3)……x(m))]。𝑌也是如此,𝑌 = [ y ( 1 ) y ( 2 ) y ( 3 ) … … y ( m ) y^{(1)} y^{(2)} y^{(3)} … … y^{(m)} y(1)y(2)y(3)……y(m)]。
所以𝑋的维数是(𝑛𝑥, 𝑚),𝑌的维数是(1, 𝑚),向量化能够让你相对较快地处理所有𝑚个样本。如果𝑚很大的话,处理速度仍然缓慢。比如说,如果𝑚是 500 万或 5000 万或者更大的一个数,在对整个训练集执行梯度下降法时,你要做的是,你必须处理整个训练集,然后才能进行一步梯度下降法,然后你需要再重新处理 500 万个训练样本,才能进行下一步梯度下降法。所以如果你在处理完整个 500 万个样本的训练集之前,先让梯度下降法处理一部分,你的算法速度会更快,准确地说,这是你可以做的一些事情。
你可以把训练集分割为小一点的子集训练,这些子集被取名为 mini-batch,假设每一个子集中只有 1000 个样本,那么把其中的 x ( 1 ) x^{(1)} x(1)到 x ( 1000 ) x^{(1000)} x(1000)取出来,将其称为第一个子训练集,也叫做 mini-batch,然后你再取出接下来的 1000 个样本,从 x ( 1001 ) x^{(1001)} x(1001)到 x ( 2000 ) x^{(2000)} x(2000),然后再取 1000个样本,以此类推。
接下来我要说一个新的符号,把 x ( 1 ) x^{(1)} x(1)到 x ( 1000 ) x^{(1000)} x(1000)称为 X 1 X^{{1}} X1, x ( 1001 ) x^{(1001)} x(1001)到 x ( 2000 ) x^{(2000)} x(2000)称为 X 2 X^{{2}} X2,如果你的训练样本一共有 500 万个,每个 mini-batch 都有 1000 个样本,也就是说,你有 5000 个mini-batch,因为 5000 乘以 1000 就是 5000 万。
你共有 5000 个 mini-batch,所以最后得到是 X 5000 X^{{5000}} X5000,对𝑌也要进行相同处理,你也要相应地拆分𝑌的训练集,所以这是 Y 1 Y^{{1}} Y1,然后从 y ( 1001 ) y^{(1001)} y(1001)到 y ( 2000 ) y^{(2000)} y(2000),这个叫 Y 2 Y^{{2}} Y2,一直到 Y 5000 Y^{{5000}} Y5000。mini-batch的数量𝑡组成了 X t X^{{t}} Xt和 Y t Y^{{t}} Yt,这就是1000个训练样本,包含相应的输入输出对。
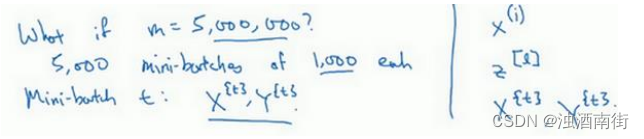
在继续课程之前,先确定一下我的符号,之前我们使用了上角小括号(𝑖)表示训练集里的值,所以 x ( i ) x^{(i)} x(i)是第𝑖个训练样本。我们用了上角中括号[𝑙]来表示神经网络的层数, z [ l ] z^{[l]} z[l]表示神经网络中第𝑙层的𝑧值,我们现在引入了大括号𝑡来代表不同的mini-batch,所以我们有 X t X^{{t}} Xt和 Y t Y^{{t}} Yt,检查一下自己是否理解无误。

X t X^{{t}} Xt和 Y t Y^{{t}} Yt的维数:如果 X 1 X^{{1}} X1是一个有 1000 个样本的训练集,或者说是 1000 个样本的𝑥值,所以维数应该是(𝑛𝑥, 1000), X 2 X^{{2}} X2的维数应该是(𝑛𝑥, 1000),以此类推。因此所有的子集维数都是(𝑛𝑥, 1000),而这些( Y t Y^{{t}} Yt的维数都是(1,1000)。
解释一下这个算法的名称,batch 梯度下降法指的是我们之前讲过的梯度下降法算法,就是同时处理整个训练集,这个名字就是来源于能够同时看到整个 batch 训练集的样本被处理,这个名字不怎么样,但就是这样叫它。
相比之下,mini-batch 梯度下降法,指的是我们在下一张幻灯片中会讲到的算法,你每次同时处理的单个的 mini-batch X t X^{{t}} Xt和 Y t Y^{{t}} Yt,而不是同时处理全部的𝑋和𝑌训练集。
那么究竟 mini-batch 梯度下降法的原理是什么?在训练集上运行 mini-batch 梯度下降法,你运行 for t=1……5000,因为我们有 5000 个各有 1000 个样本的组,在 for 循环里你要做得基本就是对 X t X^{{t}} Xt和 Y t Y^{{t}} Yt执行一步梯度下降法。假设你有一个拥有1000个样本的训练集,而且假设你已经很熟悉一次性处理完的方法,你要用向量化去几乎同时处理 1000 个样本。

首先对输入也就是 X t X^{{t}} Xt,执行前向传播,然后执行 z [ 1 ] = W [ 1 ] X + b [ 1 ] z^{[1]} = W^{[1]}X + b^{[1]} z[1]=W[1]X+b[1],之前我们这里只有,但是现在你正在处理整个训练集,你在处理第一个 mini-batch,在处理 mini-batch 时它变成了 X t X^{{t}} Xt,即 z [ 1 ] = W [ 1 ] X ( t ) + b [ 1 ] z^{[1]} = W^{[1]}X^{(t)} + b^{[1]} z[1]=W[1]X(t)+b[1],然后执行 A [ 1 ] k = g [ 1 ] ( Z [ 1 ] ) A^{[1]k} = g^{[1]}(Z^{[1]}) A[1]k=g[1](Z[1]),之所以用大写的𝑍是因为这是一个向量内涵,以此类推,直到 A [ L ] = g [ L ] ( Z [ L ] ) A^{[L]} = g^{[L]}(Z^{[L]}) A[L]=g[L](Z[L]),这就是你的预测值。注意这里你需要用到一个向量化的执行命令,这个向量化的执行命令,一次性处理 1000 个而不是 500 万个样本。
接下来你要计算损失成本函数𝐽,因为子集规模是 1000, J = 1 1000 ∑ i = 1 l L ( y ^ ( i ) , y ( i ) ) J =\frac{1}{1000}\sum_{i=1}^l{L(\hat{y}^{(i)},y^{(i)})} J=10001∑i=1lL(y^(i),y(i)) ,说明一下,这 L ( y ^ ( i ) , y ( i ) ) L(\hat{y}^{(i)},y^{(i)}) L(y^(i),y(i))指的是来自于 mini-batch X t X^{{t}} Xt和 Y t Y^{{t}} Yt中的样本。
如果你用到了正则化,你也可以使用正则化的术语:
J = 1 1000 ∑ i = 1 l L ( y ^ ( i ) , y ( i ) ) + λ 2 ∗ 1000 ∑ l ∣ ∣ w [ l ] ∣ ∣ F 2 J =\frac{1}{1000}\sum_{i=1}^l{L(\hat{y}^{(i)},y^{(i)})} + \frac{λ}{2*1000}\sum_{l}{||w^{[l]}||_F^2} J=10001∑i=1lL(y^(i),y(i))+2∗1000λ∑l∣∣w[l]∣∣F2,因为这是一个 mini-batch 的损失,所以我将𝐽损失记为上角标𝑡,放在大括号里( J = 1 1000 ∑ i = 1 l L ( y ^ ( i ) , y ( i ) ) + λ 2 ∗ 1000 ∑ l ∣ ∣ w [ l ] ∣ ∣ F 2 J =\frac{1}{1000}\sum_{i=1}^l{L(\hat{y}^{(i)},y^{(i)})} + \frac{λ}{2*1000}\sum_{l}{||w^{[l]}||_F^2} J=10001∑i=1lL(y^(i),y(i))+2∗1000λ∑l∣∣w[l]∣∣F2)。
你也会注意到,我们做的一切似曾相识,其实跟之前我们执行梯度下降法如出一辙,除了你现在的对象不是𝑋,𝑌,而是 X t X^{{t}} Xt和 Y t Y^{{t}} Yt。接下来,你执行反向传播来计算𝐽{𝑡}的梯度,你只是使用 X t X^{{t}} Xt和 Y t Y^{{t}} Yt,然后你更新加权值,𝑊实际上是 W [ l ] W^{[l]} W[l],更新为 W [ l ] : = W [ l ] − α d W [ l ] W^{[l]}: = W^{[l]} − αdW^{[l]} W[l]:=W[l]−αdW[l],对𝑏做相同处理, b [ l ] : = b [ l ] − α d b [ l ] b[l]: = b^{[l]} − αdb^{[l]} b[l]:=b[l]−αdb[l]。
这是使用 mini-batch 梯度下降法训练样本的一步,我写下的代码也可被称为进行“一代”(1 epoch)的训练。一代这个词意味着只是一次遍历了训练集。

使用 batch 梯度下降法,一次遍历训练集只能让你做一个梯度下降,使用 mini-batch 梯度下降法,一次遍历训练集,能让你做 5000 个梯度下降。当然正常来说你想要多次遍历训练集,还需要为另一个 while 循环设置另一个 for 循环。所以你可以一直处理遍历训练集,直到最后你能收敛到一个合适的精度。
如果你有一个丢失的训练集,mini-batch 梯度下降法比 batch 梯度下降法运行地更快,所以几乎每个研习深度学习的人在训练巨大的数据集时都会用到,下一个视频中,我们将进一步深度讨论 mini-batch 梯度下降法,你也会因此更好地理解它的作用和原理。
2.2 理解 mini-batch 梯度下降法(Understanding mini-batch gradient descent)
在上周视频中,你知道了如何利用 mini-batch 梯度下降法来开始处理训练集和开始梯度下降,即使你只处理了部分训练集,即使你是第一次处理,本视频中,我们将进一步学习如何执行梯度下降法,更好地理解其作用和原理。
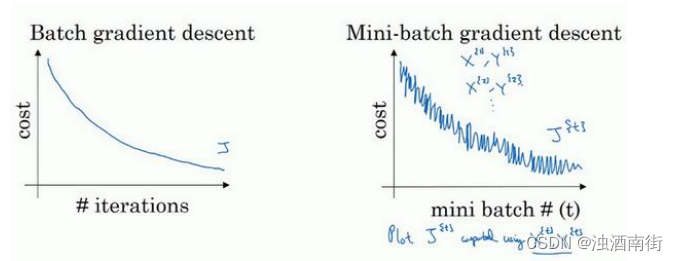
使用 batch 梯度下降法时,每次迭代你都需要历遍整个训练集,可以预期每次迭代成本都会下降,所以如果成本函数𝐽是迭代次数的一个函数,它应该会随着每次迭代而减少,如果𝐽在某次迭代中增加了,那肯定出了问题,也许你的学习率太大。
使用 mini-batch 梯度下降法,如果你作出成本函数在整个过程中的图,则并不是每次迭代都是下降的,特别是在每次迭代中,你要处理的是 X t X^{{t}} Xt和 Y t Y^{{t}} Yt,如果要作出成本函数 J t J^{{t}} Jt的图,而 J t J^{{t}} Jt只和 X t X^{{t}} Xt, Y t Y^{{t}} Yt有关,也就是每次迭代下你都在训练不同的样本集或者说训练不同的 mini-batch,如果你要作出成本函数𝐽的图,你很可能会看到这样的结果,走向朝下,但有更多的噪声,所以如果你作出 Y t Y^{{t}} Yt的图,因为在训练 mini-batch 梯度下降法时,会经过多代,你可能会看到这样的曲线。没有每次迭代都下降是不要紧的,但走势应该向下,噪声产生的原因在于也许 X t X^{{t}} Xt和 Y t Y^{{t}} Yt是比较容易计算的 mini-batch,因此成本会低一些。不过也许出于偶然, X 2 X^{{2}} X2和 Y 2 Y^{{2}} Y2是比较难运算的 mini-batch,或许你需要一些残缺的样本,这样一来,成本会更高一些,所以才会出现这些摆动,因为你是在运行 mini-batch 梯度下降法作出成本函数图。
你需要决定的变量之一是 mini-batch 的大小,𝑚就是训练集的大小,极端情况下:
如果 mini-batch 的大小等于𝑚,其实就是 batch 梯度下降法,在这种极端情况下,你就有了 mini-batch X 1 X^{{1}} X1和 Y 1 Y^{{1}} Y1,并且该 mini-batch 等于整个训练集,所以把 mini-batch 大小设为𝑚可以得到 batch 梯度下降法。
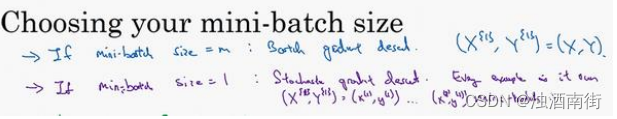
另一个极端情况,假设 mini-batch 大小为 1,就有了新的算法,叫做随机梯度下降法,每个样本都是独立的 mini-batch,当你看第一个 mini-batch,也就是 X 1 X^{{1}} X1和 Y 1 Y^{{1}} Y1,如果 mini-batch 大小为 1,它就是你的第一个训练样本,这就是你的第一个训练样本。接着再看第二个 mini-batch,也就是第二个训练样本,采取梯度下降步骤,然后是第三个训练样本,以此类推,一次只处理一个。
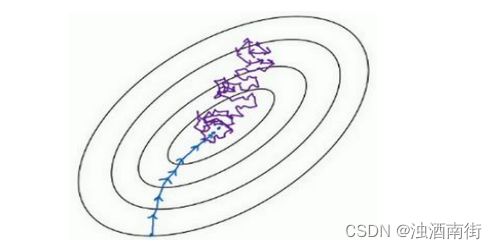
看在两种极端下成本函数的优化情况,如果这是你想要最小化的成本函数的轮廓,最小值在那里,batch 梯度下降法从某处开始,相对噪声低些,幅度也大一些,你可以继续找最小值。
相反,在随机梯度下降法中,从某一点开始,我们重新选取一个起始点,每次迭代,你只对一个样本进行梯度下降,大部分时候你向着全局最小值靠近,有时候你会远离最小值,因为那个样本恰好给你指的方向不对,因此随机梯度下降法是有很多噪声的,平均来看,它最终会靠近最小值,不过有时候也会方向错误,因为随机梯度下降法永远不会收敛,而是会一直在最小值附近波动,但它并不会在达到最小值并停留在此。
实际上你选择的 mini-batch 大小在二者之间,大小在 1 和𝑚之间,而 1 太小了,𝑚太大了,原因在于如果使用 batch 梯度下降法,mini-batch 的大小为𝑚,每个迭代需要处理大量训练样本,该算法的主要弊端在于特别是在训练样本数量巨大的时候,单次迭代耗时太长。如果训练样本不大,batch 梯度下降法运行地很好。

相反,如果使用随机梯度下降法,如果你只要处理一个样本,那这个方法很好,这样做没有问题,通过减小学习率,噪声会被改善或有所减小,但随机梯度下降法的一大缺点是,你会失去所有向量化带给你的加速,因为一次性只处理了一个训练样本,这样效率过于低下,所以实践中最好选择不大不小的 mini-batch 尺寸,实际上学习率达到最快。你会发现两个好处,一方面,你得到了大量向量化,上个视频中我们用过的例子中,如果 mini-batch 大小为1000 个样本,你就可以对 1000 个样本向量化,比你一次性处理多个样本快得多。另一方面,你不需要等待整个训练集被处理完就可以开始进行后续工作,再用一下上个视频的数字,每次训练集允许我们采取 5000 个梯度下降步骤,所以实际上一些位于中间的 mini-batch 大小效果最好。
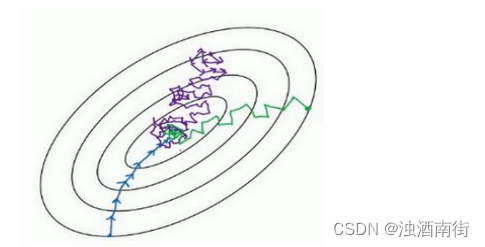
用 mini-batch 梯度下降法,我们从这里开始,一次迭代这样做,两次,三次,四次,它不会总朝向最小值靠近,但它比随机梯度下降要更持续地靠近最小值的方向,它也不一定在很小的范围内收敛或者波动,如果出现这个问题,可以慢慢减少学习率,我们在下个视频会讲到学习率衰减,也就是如何减小学习率。
如果 mini-batch 大小既不是 1 也不是𝑚,应该取中间值,那应该怎么选择呢?其实是有指导原则的。
首先,如果训练集较小,直接使用 batch 梯度下降法,样本集较小就没必要使用 minibatch 梯度下降法,你可以快速处理整个训练集,所以使用 batch 梯度下降法也很好,这里的少是说小于 2000 个样本,这样比较适合使用 batch 梯度下降法。不然,样本数目较大的话,一般的 mini-batch 大小为 64 到 512,考虑到电脑内存设置和使用的方式,如果 minibatch 大小是 2 的𝑛次方,代码会运行地快一些,64 就是 2 的 6 次方,以此类推,128 是 2 的7 次方,256 是 2 的 8 次方,512 是 2 的 9 次方。所以我经常把 mini-batch 大小设成 2 的次方。在上一个视频里,我的 mini-batch 大小设为了 1000,建议你可以试一下 1024,也就是2 的 10 次方。也有 mini-batch 的大小为 1024,不过比较少见,64 到 512 的 mini-batch 比较常见。
最后需要注意的是在你的 mini-batch 中,要确保𝑋{𝑡}和𝑌{𝑡}要符合 CPU/GPU 内存,取决于你的应用方向以及训练集的大小。如果你处理的 mini-batch 和 CPU/GPU 内存不相符,不管你用什么方法处理数据,你会注意到算法的表现急转直下变得惨不忍睹,所以我希望你对一般人们使用的 mini-batch 大小有一个直观了解。事实上 mini-batch 大小是另一个重要的变量,你需要做一个快速尝试,才能找到能够最有效地减少成本函数的那个,我一般会尝试几个不同的值,几个不同的 2 次方,然后看能否找到一个让梯度下降优化算法最高效的大小。希望这些能够指导你如何开始找到这一数值。
你学会了如何执行 mini-batch 梯度下降,令算法运行得更快,特别是在训练样本数目较大的情况下。不过还有个更高效的算法,比梯度下降法和 mini-batch 梯度下降法都要高效的多,我们在接下来的视频中将为大家一一讲解。