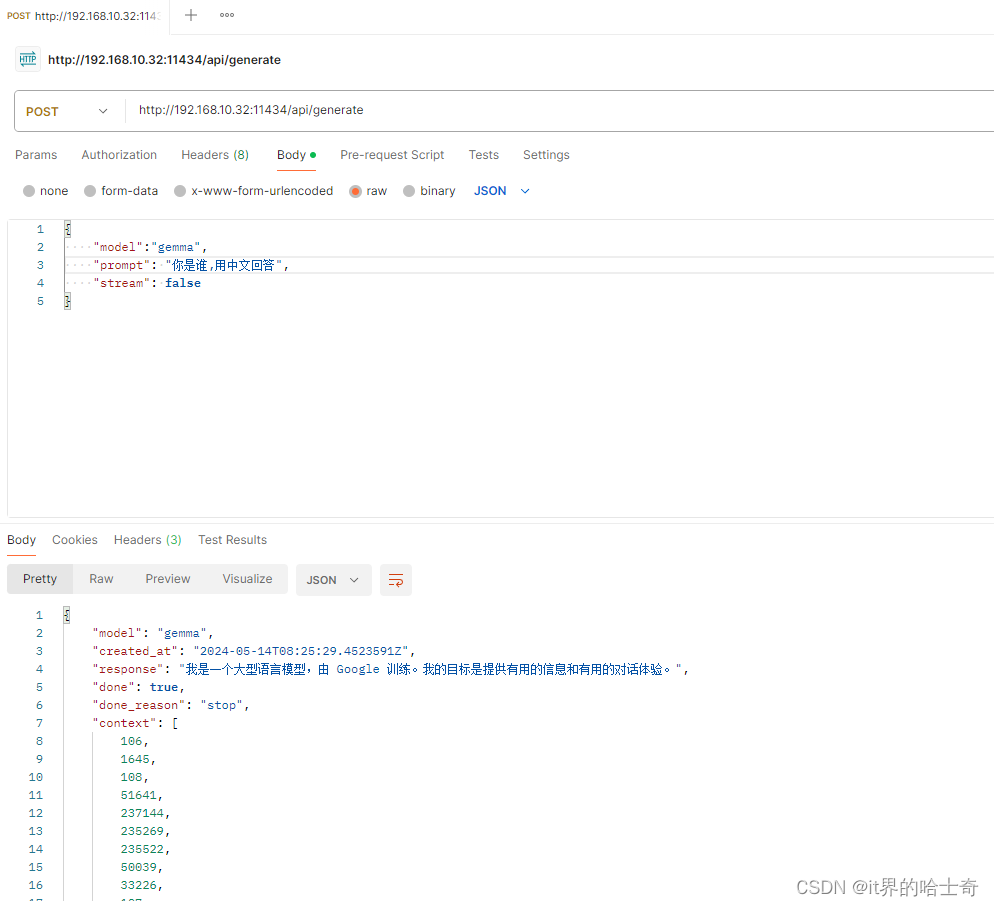
比赛经历:2024.5.14简单vp了一个小时只写出了签到题4个然后跑路了

补题:感觉其他题有点太抽象了主要补了一题,在区间问题中数据结构的使用
比赛链接[点我即可]
目录
A.欢迎来到辽宁省赛
B.胜率
F.隔板与水槽
H.取石子
L.区间与绝对值
M.让二追三
A.欢迎来到辽宁省赛
void solve(){cout << 27 << endl;return ;
}没啥好说的直接输出即可
B.胜率
我们首先看一下是最后答案是四舍五入保留两位小数,可以判断出来答案一定是在10000局可以做到的,同时小数并不好判断我们直接把小数变成整数跑循环暴力找答案即可
// 数学公式要变形
// 莫急莫急先读题
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&(-x))
#define endl "\n"
#define ios ios::sync_with_stdio(0); cin.tie(0),cout.tie(0);
#define LF(x) fixed<<setprecision(x)// c++ 保留小数
#define den(a) cout << #a << " = " << a << "\n";
#define deg(a) cout << #a << " = " << a << " ";
typedef long long LL;
typedef pair<int, int> PII;
const int N=1000010,M=10010,INF=0x3f3f3f3f,mod=1e9+7;
const double pai=acos(-1.0);// pai
map<int,int> mp;
int t,n,m;
const double esp = 1e-3;
void solve(){int pos = M;double res; cin>>res;int t = res * 100;for(int i=0;i<M;i++){for(int j=1;j<M;j++){double now = 1.0*i/j*100;now += 0.005;int yes = now*100;if(yes==t){pos = min(pos,j);}}}cout << pos << endl;return ;
}
signed main ()
{ios// 不能有printf puts scanfint t=1;while(t--){solve();}
}
F.隔板与水槽
我们观察数据范围可以发现应该在级别,同时左右是独立的,所以我们可以枚举中间位置去记录其左右最大值即可
LL a[N];
LL L[N],R[N];void solve(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];for(int i=2;i<=n;i++){for(int j=1;j<i;j++){L[i]=max(L[i],min(a[i],a[j])*(i-j));}}for(int i=n-1;i>=1;i--){for(int j=n;j>i;j--){R[i]=max(R[i],min(a[i],a[j])*(j-i));}}LL ans = 0;for(int i=2;i<n;i++) ans = max(ans,L[i]+R[i]);cout << ans << endl;return ;
}H.取石子
我们通过对式子分析可以得出,无论如何选择,两个人能取出的石头都是奇数个数,那么结果就之和给出的奇偶有关系了,简单做个判断即可
void solve(){int a,b,n; cin>>a>>b>>n;cout << (n&1? "Alice" : "Bob") << endl;return ;
}L.区间与绝对值
对于区间问题我们如果有式子可以简单推理一下,由式子得到就是区间中的每一个数互相做减法的绝对值之和,我们看一下对于一个区间如何计算贡献,不妨这样想如果我把右端点加一个数如何计算新的区间贡献,可以发现新来的数带来的贡献为
int g[N],a[N];
LL tr[N][2],res[N],ans;
struct code{int l,r,id;bool operator<(const code&t)const{return g[l]==g[t.l] ? r<t.r : l < t.l;}
}Q[N];
void add(int op,int k,int x){for(int i=k;i<N;i+=lowbit(i)) tr[i][op]+=x;
}
LL query(int op,int k){LL res = 0;for(int i=k;i;i-=lowbit(i)) res += tr[i][op];return res;
}
void add(int x){x = a[x];ans += query(0,x-1)*x - query(1,x-1);ans += (query(1,N-1)-query(1,x)) - (query(0,N-1)-query(0,x))*x;add(0,x,1);add(1,x,x);
}
void del(int x){x = a[x];ans -= query(0,x-1)*x - query(1,x-1);ans -= (query(1,N-1)-query(1,x)) - (query(0,N-1)-query(0,x))*x;add(0,x,-1);add(1,x,-x);
}
void solve(){cin>>n>>m;int block = sqrt(n);for(int i=1;i<=n;i++){cin>>a[i];g[i]=(i-1)/block+1;}for(int i=1;i<=m;i++){int l,r; cin>>l>>r;Q[i]={l,r,i};}sort(Q+1,Q+1+m);int L = 1 ,R = 0;for(int i=1;i<=m;i++){auto [l,r,id]=Q[i];while(L<l) del(L++);while(L>l) add(--L);while(R>r) del(R--);while(R<r) add(++R);res[id]=2*ans;}for(int i=1;i<=m;i++) cout << res[i] << endl;return ;
}这样的话我们可以发现实际上维护的就是区间中小于这个数的数量,和小于这个数的和,可以知道树状数组就具有这个功能,但是对于多个区间如何操作,我们可以看到时间是4s,那么对于多个区间问题我们可以考虑使用莫队算法来优化本题
最后时间复杂度就是
M.让二追三
概率可以直接按照一次比赛打五次直接算出来,但是注意的是在n个比赛中,那么当n<5时是无解的,大于5的时候有n-4个符合题意的可以
LL qmi(LL a,LL b,LL p){LL res = 1;while(b){if(b&1) res=res*a%p;b>>=1;a=a*a%p;}return res;
}
LL inv(LL x){return qmi(x,mod-2,mod);
}
void solve(){int a,b,n; cin>>a>>b>>n;if(n<5){cout << 0 << endl;return ;}LL fm = qmi(b,5,mod);LL fz = qmi(b-a,2,mod)*qmi(a,3,mod)%mod;LL ans = fz%mod*inv(fm)%mod*(n-4)%mod; // 每次发生的概率是一样的// 就是cout << ans << endl;return ;
}