LeetCode算法题：11. 盛最多水的容器（Java）（双指针问题总结）-编程知识

LeetCode算法题：11. 盛最多水的容器（Java）（双指针问题总结）

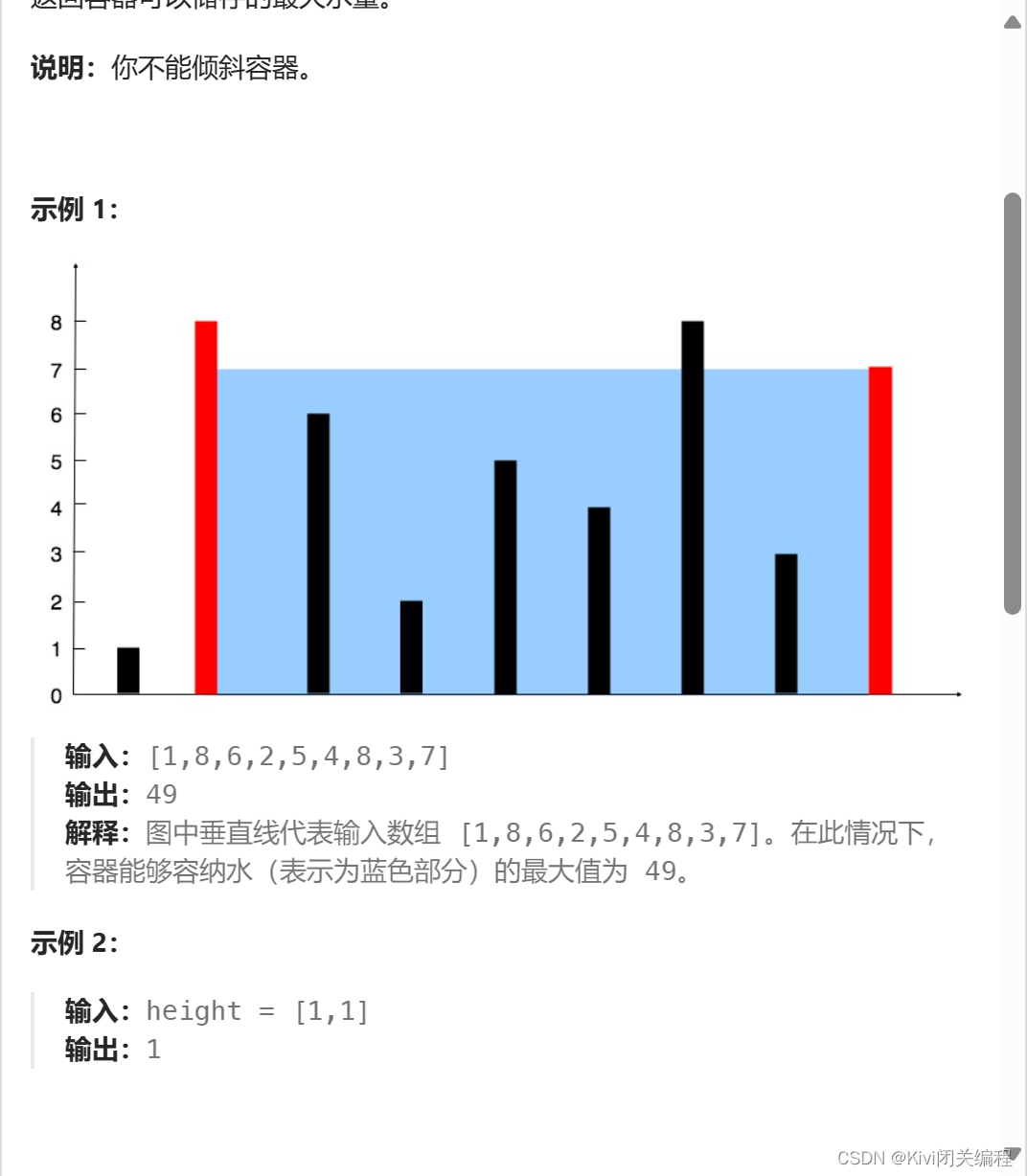
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

在这里插入图片描述

提示：

n == height.length
2 <= n <= 10^5
0 <= height[i] <= 10^4

解题思路：

定义两个指针啊a，b分别指向height数组的第一个元素和第二个元素，表示容器的左边和容器右边，定义一个maxVolume表示记录的最大容量，初始定义为0。定义两层循环，外层循环a指针，内层循环b指针，如果当a，b指针所形成容器的容量大于maxVolume时更新maxVolume。遍历完之后找到最大值。

class Solution {public int maxArea(int[] height) {int maxVolume = 0;for(int a=0;a<height.length;a++){for(int b=a+1;b<height.length;b++){if(((b-a)*Math.min(height[a],height[b]))>maxVolume)maxVolume = (b-a)*Math.min(height[a],height[b]);}}return maxVolume;}
}

时间复杂度为O(n^2),空间复杂度为O(1)。提交报错：
在这里插入图片描述
时间复杂度过高，得想办法降低时间复杂度。

修改思路：

初始化定义两个指针a,b分别指向height数组第一个元素和最后一个元素。初始化maxVolume等于height[a]*height[b]表示当前最大容量，分析一下可以知道，当前状态的容量底宽是最宽的情况了，那么容量的大小，取决于左边和后边较矮的边。例如如果当前是a,b所指高度是a所指高度较矮，那么要做到下一次找到的容器比原来的大，只能是找到一个更高的左边才有可能。同理，如果是右边更矮，则要找到一个更高的右边才行。因此每次移动较矮的那一边，如果是左边更矮，则向右移，找到一个比原来左边高的边，重新计算容量；如果是右边更矮，则向左移，找到一个比原来右边高的边。重新计算容量，如果比之前容量大，则更新maxVolume。直到左边指针越过右边指针，则停下。当前maxVolume是最大的容量。

代码：

class Solution {public int maxArea(int[] height) {int a=0,b=height.length-1;int maxVolume=(b-a)*(Math.min(height[a],height[b]));int maxLeftEdge = height[a],maxRightEdge = height[b];while(a<b){if(height[a]<height[b]){a = a+1;while(height[a]<=maxLeftEdge&&a<b)a=a+1;}else{b = b-1;while(height[b]<=maxRightEdge&&a<b)b=b-1;}if((b-a)*(Math.min(height[a],height[b]))>maxVolume){maxVolume = (b-a)*(Math.min(height[a],height[b]));maxLeftEdge = height[a];maxRightEdge = height[b];}}return maxVolume;}
}

结果：

在这里插入图片描述

上述算法时间复杂度为O(n)，空间复杂度为O(1)。
但是看到时间复杂度依然有改进空间。查看1ms时间复杂度的代码：

class Solution {public int maxArea(int[] height) {int l =0,r =height.length-1;int max =0;while(l<r){if(height[r]>height[l]){max = Math.max(max,(r-l)*height[l]);int tmp = height[l];while(tmp>= height[l]&&l<r) l++;}else{max = Math.max(max,(r-l)*height[r]);int tmp = height[r];while(tmp>= height[r]&&l<r) r--;}}return max;}
}