机器学习中10种损失函数大梳理！建议收藏，你一定用得到-编程知识

机器学习中10种损失函数大梳理！建议收藏，你一定用得到

接上篇：机器学习中10种损失函数大梳理！建议收藏，你一定用得到-CSDN博客

8、希尔伯特-施密特口袋

希尔伯特-施密特口袋（Hinge-Schmidt Pocket）是一种用于支持向量机训练的损失函数。它是一种改进的希尔伯特-施密特损失函数，旨在更好地处理线性可分和线性不可分问题。

在解释希尔伯特-施密特口袋之前，我们先来了解一下标准的希尔伯特-施密特损失函数。

希尔伯特-施密特损失函数

希尔伯特-施密特损失函数是SVM中常用的损失函数之一，用于二分类问题的训练。其主要思想是要找到一个超平面，将两个类别的数据分开，并最大化这个超平面与最近的数据点（支持向量）之间的间隔。

损失函数的公式：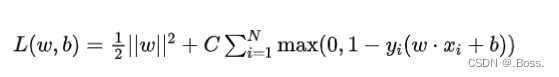

下面我们将演示如何使用Python和Scikit-Learn来执行一个简单的二分类问题，使用交叉熵损失函数来训练一个逻辑回归模型，并绘制决策边界的图形。

首先，我们需要导入必要的库和生成一些模拟数据。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression# 生成模拟数据
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_classes=2, random_state=42)# 创建逻辑回归模型
model = LogisticRegression()# 训练模型
model.fit(X, y)# 用于绘制决策边界的辅助函数
def plot_decision_boundary(X, y, model):xx, yy = np.meshgrid(np.linspace(X[:, 0].min() - 1, X[:, 0].max() + 1, 100),np.linspace(X[:, 1].min() - 1, X[:, 1].max() + 1, 100))Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.8)plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.show()# 绘制决策边界
plot_decision_boundary(X, y, model)

这段代码生成了一个二维的模拟数据集，使用Scikit-Learn的逻辑回归模型进行训练，并绘制了决策边界的图形。决策边界将两个类别的数据分开。

交叉熵损失在逻辑回归模型中是默认的损失函数，它在模型训练过程中最小化损失来找到最佳的参数（权重和偏置）。

9、Huber损失

Huber损失是一种用于回归问题的损失函数，它对异常值不敏感，相比于均方误差（MSE），它对异常值的惩罚较小。Huber损失的主要思想是在距离真实值较近的情况下采用均方误差，而在距离较远的情况下采用绝对误差，这种权衡可以有效减少异常值的影响。

Huber损失的公式：

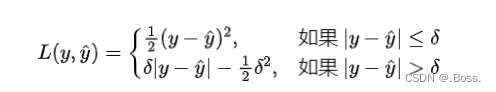
import numpy as np
import matplotlib.pyplot as plt# 定义Huber损失函数
def huber_loss(y_true, y_pred, delta):error = np.abs(y_true - y_pred)if error <= delta:return 0.5 * error**2else:return delta * error - 0.5 * delta**2# 生成一些样本数据
np.random.seed(0)
X = np.linspace(0, 10, 100)
y_true = 2 * X + 1 + np.random.normal(0, 1, 100)# 定义模型预测值
y_pred = 2 * X + 1# 计算不同delta值下的损失
deltas = [1.0, 2.0, 5.0]
losses = []for delta in deltas:loss = [huber_loss(y_true[i], y_pred[i], delta) for i in range(len(X))]losses.append(loss)# 绘制损失曲线
plt.figure(figsize=(10, 6))
for i, delta in enumerate(deltas):plt.plot(X, losses[i], label=f'Huber Loss (delta={delta})')plt.xlabel('X')
plt.ylabel('Loss')
plt.title('Huber Loss for Different Delta Values')
plt.legend()
plt.grid(True)
plt.show()

代码中，首先定义了Huber损失函数，然后生成了一些样本数据，包括真实的目标值和模型的预测值。接下来，我们计算了不同delta值下的损失，并绘制了损失曲线。从图中可以清晰地看出，随着delta值的增大，Huber损失在异常值处的惩罚逐渐减小，这是Huber损失相对于均方误差的一个重要特点。

以上示例说明了Huber损失如何在不同情况下平衡均方误差和绝对误差，以减少异常值对损失的影响。

10、感知器损失

感知器损失函数，也称为0-1损失函数，是一种用于二元分类任务的损失函数。

它的原理非常简单：它将分类问题的输出与真实标签进行比较，如果预测正确则损失为0，否则损失为1。

感知器损失函数的公式：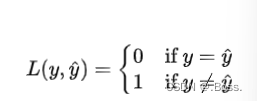

import numpy as np
import matplotlib.pyplot as plt# Generate random binary classification dataset
np.random.seed(0)
X = np.random.rand(100, 2)  # 100 samples with 2 features each
y = (X[:, 0] + X[:, 1] > 1).astype(int)  # Labels: 1 if sum of features > 1, else 0# Assume our model always predicts 1 for demonstration
y_pred = np.ones_like(y)# Calculate perceptron loss
loss = np.mean(np.abs(y - y_pred))# Print the loss value
print(f"Perceptron Loss: {loss}")# Plot data points and decision boundary
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Binary Classification Dataset and Decision Boundary")# Plot the decision boundary (a simple straight line here)
x_line = np.linspace(0, 1.2, 100)
y_line = 1 - x_line
plt.plot(x_line, y_line, 'k--', label="Decision Boundary")
plt.legend()
plt.show()

当然，在特定的场景和条件下，很大情况下需要自定义损失函数~