一、题目描述

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

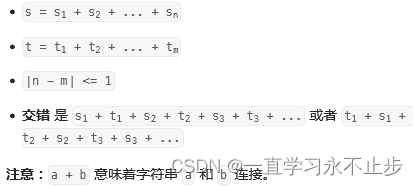
两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空

子字符串：

示例 1：

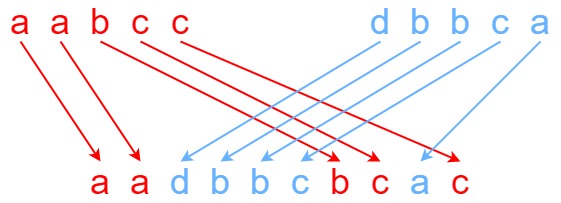
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true

示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出：false

示例 3：

输入：s1 = "", s2 = "", s3 = ""
输出：true

提示：

• 0 <= s1.length, s2.length <= 100
• 0 <= s3.length <= 200
• s1、s2、和 s3 都由小写英文字母组成

二、解题思路

1. 状态定义：创建一个二维布尔数组 dp，其中 dp[i][j] 表示 s1 的前 i 个字符和 s2 的前 j 个字符是否能交错组成 s3 的前 i+j 个字符。

2. 状态转移方程：对于 dp[i][j]，它可以从两个状态转移而来：

• dp[i-1][j] 且 s1[i-1] == s3[i+j-1]，这意味着 s1 的第 i-1 个字符和 s3 的第 i+j-1 个字符相同，那么如果 dp[i-1][j] 为真，dp[i][j] 也为真。
• dp[i][j-1] 且 s2[j-1] == s3[i+j-1]，这意味着 s2 的第 j-1 个字符和 s3 的第 i+j-1 个字符相同，那么如果 dp[i][j-1] 为真，dp[i][j] 也为真。

3. 初始化：dp[0][0] 应该初始化为 true，因为没有字符的情况下，当然可以构成一个空字符串。对于第一行和第一列，我们需要检查 s1 和 s3 以及 s2 和 s3 的对应字符是否相等。

4. 结果：dp[s1.length()][s2.length()] 的值就是最终结果。

三、具体代码

class Solution {public boolean isInterleave(String s1, String s2, String s3) {int len1 = s1.length();int len2 = s2.length();int len3 = s3.length();// 如果 s1 和 s2 的长度之和与 s3 的长度不相等，那么 s3 不能由 s1 和 s2 交错组成if (len1 + len2 != len3) {return false;}// dp[i][j] 表示 s1 的前 i 个字符和 s2 的前 j 个字符是否能交错组成 s3 的前 i+j 个字符boolean[][] dp = new boolean[len1 + 1][len2 + 1];// 初始化 dp 数组dp[0][0] = true;for (int i = 1; i <= len1; i++) {dp[i][0] = dp[i - 1][0] && s1.charAt(i - 1) == s3.charAt(i - 1);}for (int j = 1; j <= len2; j++) {dp[0][j] = dp[0][j - 1] && s2.charAt(j - 1) == s3.charAt(j - 1);}// 状态转移for (int i = 1; i <= len1; i++) {for (int j = 1; j <= len2; j++) {dp[i][j] = (dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(i + j - 1)) ||(dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(i + j - 1));}}// 返回结果return dp[len1][len2];}
}

四、时间复杂度和空间复杂度

1. 时间复杂度

• 初始化 dp 数组的时间复杂度为 O(1)，因为只设置了数组的两个边界。
• 接下来的两个循环用于填充 dp 数组的边界，每个循环的时间复杂度分别为 O(len1) 和 O(len2)。
• 最后的两个嵌套循环用于根据状态转移方程填充 dp 数组的其余部分，时间复杂度为 O(len1 * len2)。
• 综上所述，总的时间复杂度为 O(len1 + len2 + len1 * len2)，由于在实际情况中，len1 * len2 的项通常比 len1 和 len2 大得多，因此可以简化为 O(len1 * len2)。

2. 空间复杂度

• dp 数组的大小为 (len1 + 1) x (len2 + 1)，因此空间复杂度为 O(len1 * len2)。

综上所述，代码的时间复杂度为 O(len1 * len2)，空间复杂度也为 O(len1 * len2)。

五、总结知识点

1. 字符串操作：

• 使用 length() 方法获取字符串的长度。
• 使用 charAt(index) 方法获取字符串中指定索引处的字符。

2. 动态规划（Dynamic Programming）：

• 使用二维数组 dp 来存储子问题的解，避免重复计算。
• 定义状态 dp[i][j] 表示 s1 的前 i 个字符和 s2 的前 j 个字符是否能交错组成 s3 的前 i+j 个字符。
• 状态转移方程基于上一个状态和当前字符的比较。

3. 边界条件处理：

• 检查 s1 和 s2 的长度之和是否等于 s3 的长度，如果不等，直接返回 false。
• 初始化 dp 数组的边界值，即第一行和第一列，这代表了一个字符串为空时的情况。

4. 逻辑运算：

• 使用逻辑与运算符 && 来组合条件表达式。
• 使用逻辑或运算符 || 在状态转移方程中提供两种可能的转移路径。

5. 循环结构：

• 使用嵌套的 for 循环来遍历 s1 和 s2 的所有可能的前缀组合。

6. 数组操作：

• 创建并初始化二维布尔数组 dp。
• 通过索引访问和更新数组中的元素。

7. 算法设计：

• 使用自底向上的方法来填充动态规划表格，这是一种常见的动态规划策略。

8. 问题求解：

• 将给定的问题分解为更小的子问题，并通过组合子问题的解来求解原问题。

以上就是解决这个问题的详细步骤，希望能够为各位提供启发和帮助。