在说多线程操作List之前,我们先看下单线程下产生的问题:
单线程
List<Integer> listA=new ArrayList<>();
listA.add(1);
listA.add(2);
listA.add(3);
listA.add(4);
listA.add(5);
listA.add(6);
for(Integer a:listA){
if (a==3) {
listA.remove(3);
}
}
//再次使用集合就会报错
System.out.println("list元素:" + listA);
该段代码最终会抛出 java.util.ConcurrentModificationException 错误,主要的原因是:
在List循环时,会初始化modCount=0;当该集合进行增加、删除操作值,modCount会自增;而我们使用加强for循环时候,会把modCount初始化的值给迭代器中的expectedModCount,也就是说开始expectedModCount也是为0;但是当集合操作了新增元素,modCount++ ,但是expectedModCount没有新增。导致modCount和expectedModCount不一致,当我们再次访问这个原集合时候,就会抛出java.util.ConcurrentModificationException 错误。
多线程
说明:subList 返回的是 ArrayList 的内部类 SubList,并不是ArrayList ,而是 ArrayList 的一个视图,对于SubList子列表的所有操作最终会反映到原列表上,对SubList操作,其实也是对ArrayList 操作,比如删除SubList中的元素,同时也会删除ArrayList 的元素。 在subList场景中,高度注意对父集合元素的增加或删除,均会导致子列表的遍历、增加、删除产生 ConcurrentModificationException 异常。
List<Integer> arrayList = new ArrayList<>();arrayList.add(1);arrayList.add(2);arrayList.add(3);arrayList.add(4);arrayList.add(5);arrayList.add(6);Thread t1= new Thread(new Runnable() {@Overridepublic void run() {List<Integer> list = arrayList.subList(0, 3);for (Integer integer : list) {System.out.println(" "+integer);if(integer == 2){list.remove(integer);}}System.out.println("进行元素的删除操作");//arrayList.remove(4);System.out.println("list元素:" + list);}});Thread t2= new Thread(new Runnable() {@Overridepublic void run() {List<Integer> list2 = arrayList.subList(4, 6);for (Integer integer : list2) {System.out.println(" "+integer);if(integer == 4){list2.remove(integer);}}System.out.println("进行元素的删除操作");//arrayList.remove(4);System.out.println("list元素:" + list2);}});t1.start();t2.start();
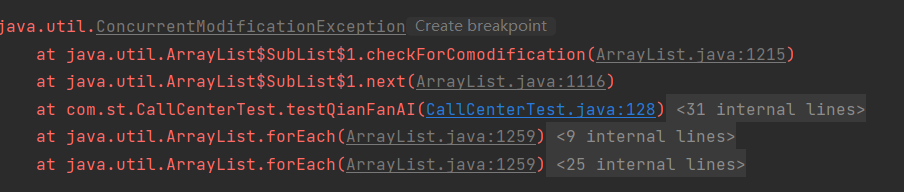
ArrayList中有个protected transient int modCount = 0; 用来记录当前ArrayList被修改的次数。
比如add(),remove()等都会导致modeCount增加: ArrayList.subList()会生成一个SubList的对象,SubList中有个对应modCount同步ArrayList中的modeCount: SubList对象每次再遍历时,会将自己的modeCount与ArrayList的modeCount进行对比,如果两个值不一样就会报异常:ConcurrentModificationException