【Linux】《VMware17搭建Ubuntu.22.04-Rust开发环境》

下载VMware17安装包

下载链接：

创建虚拟机

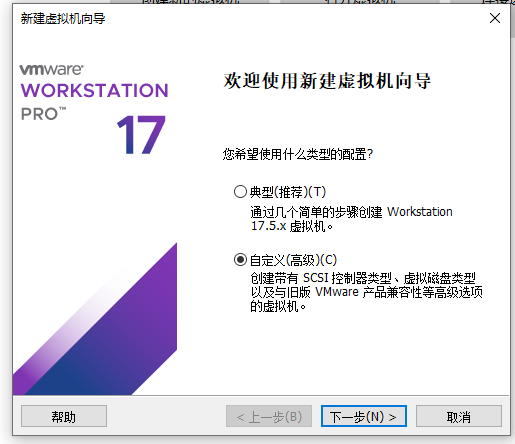
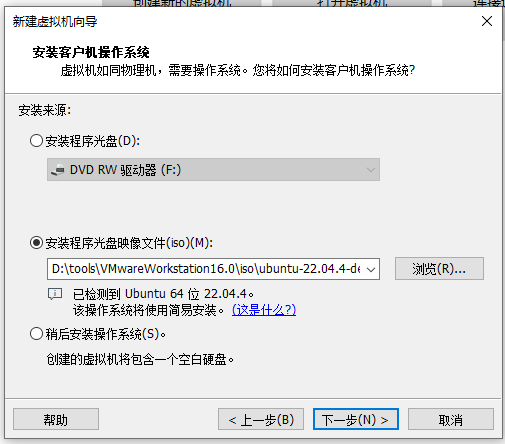
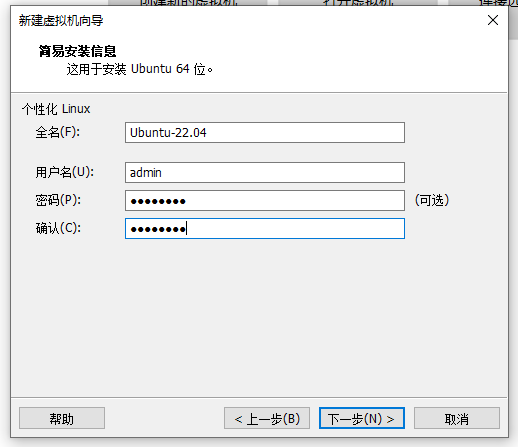
之后都默认就可以了。进入系统设置登录账号和密码以及修改下语言，剩余都默认即可。

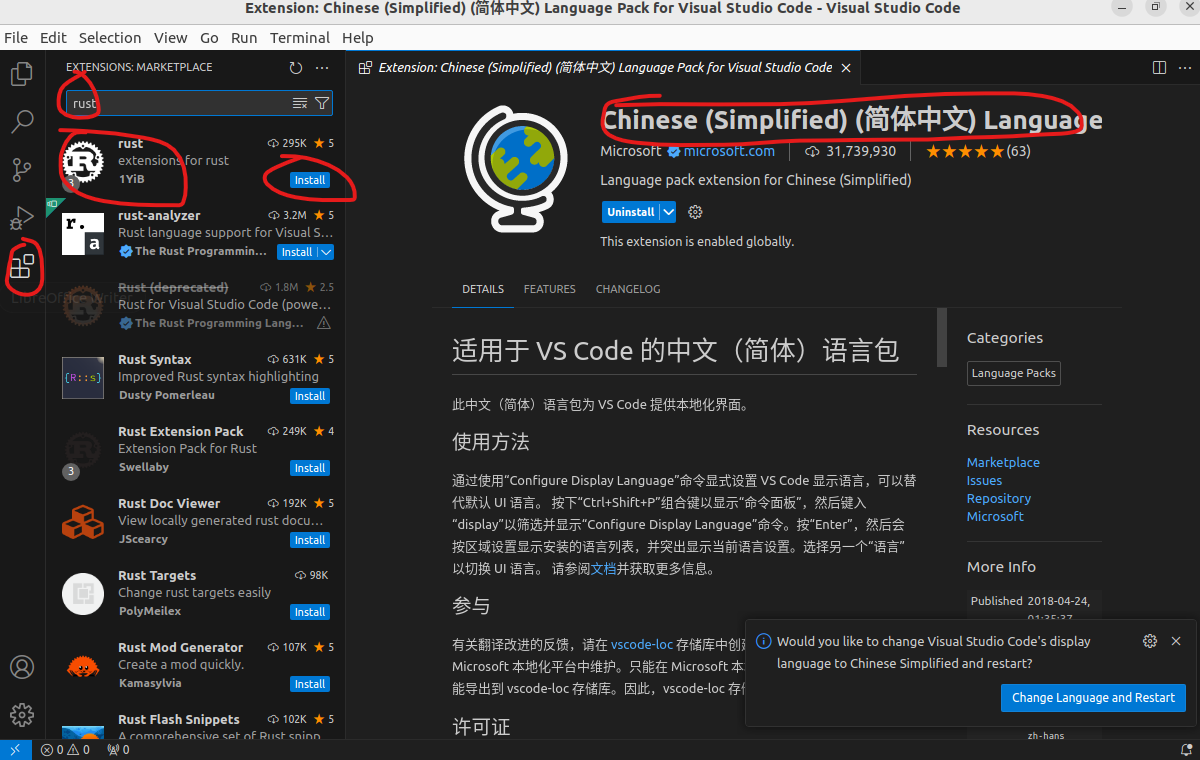
设置中文界面

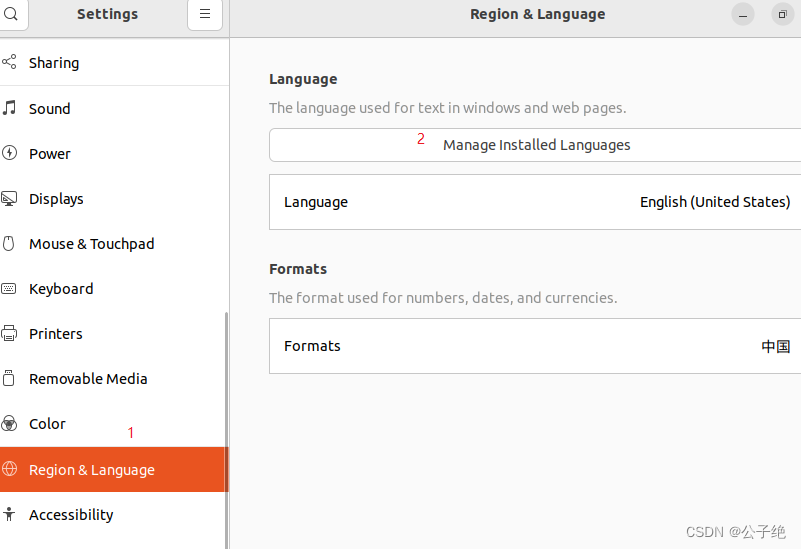
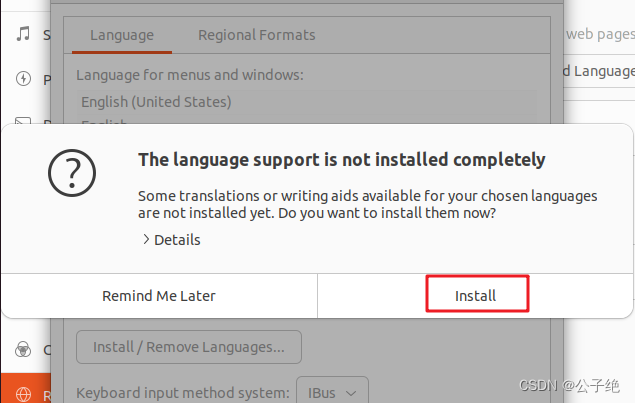
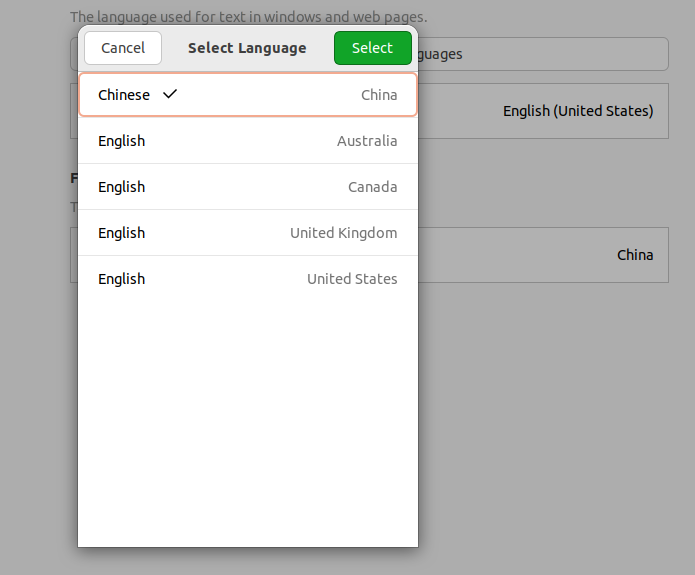
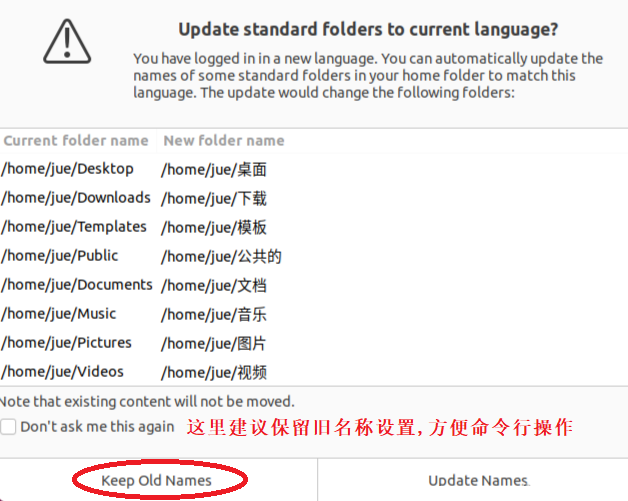
设置中文输入法

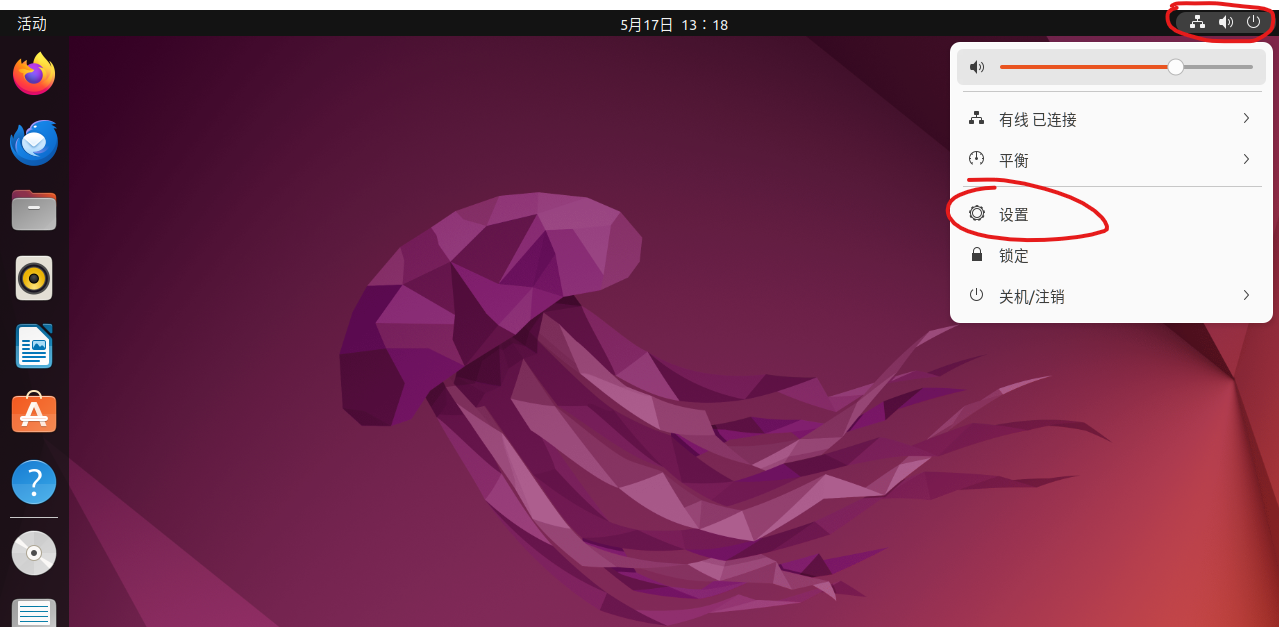
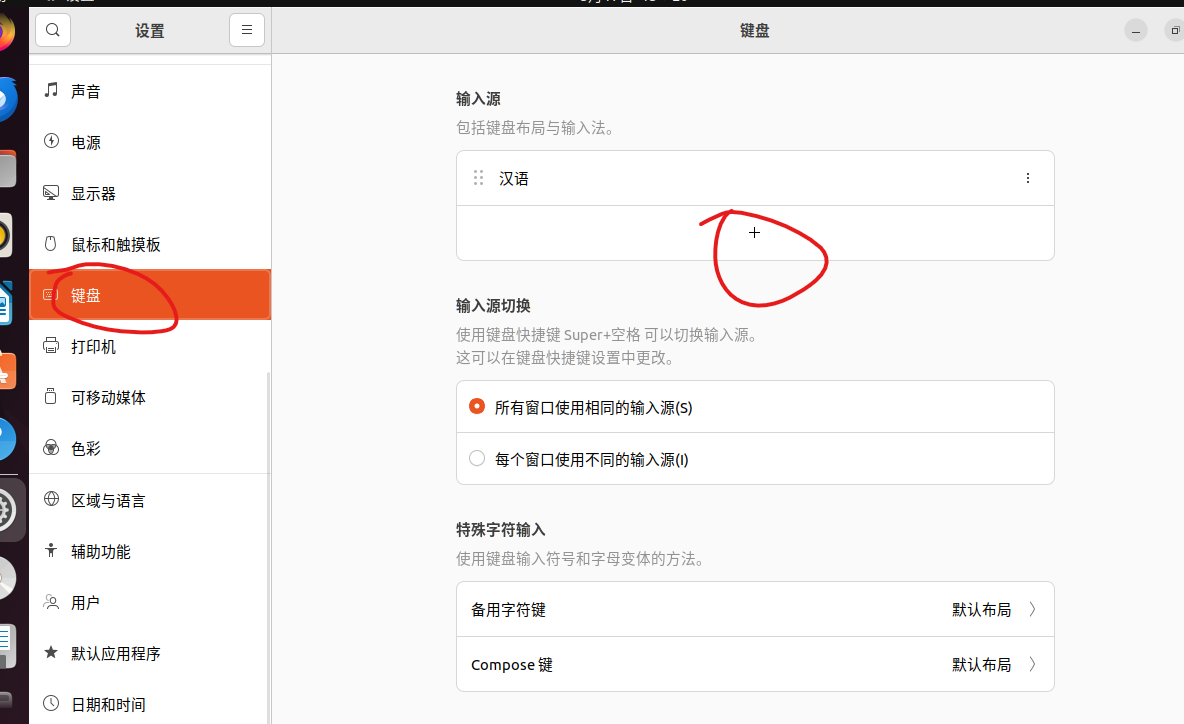
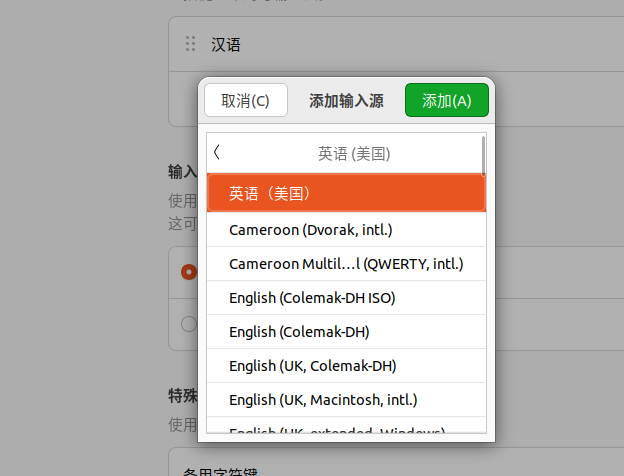
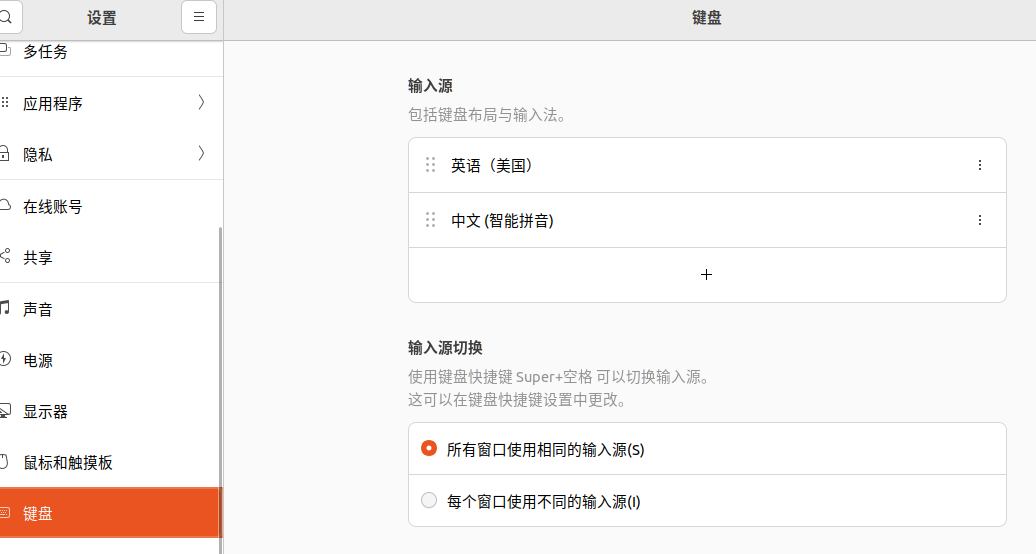
接下来开始设置输入法切换快捷键设置

使用 Ctrl + Alt + T 打开终端，输入 ibus-setup

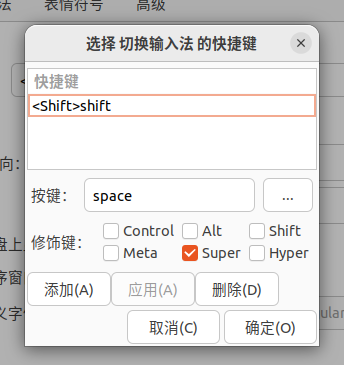
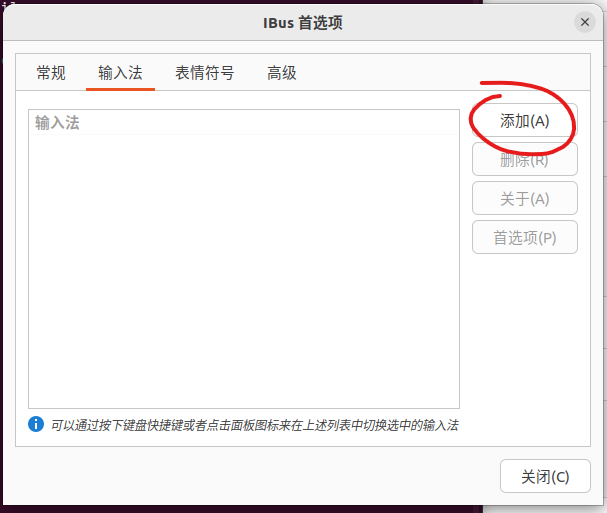
重启，看一下是否有输入法信息

尝试手动点击切换一下输入法，然后再尝试快捷键切换一下。

更换更新源

使用快捷键 Ctrl + Alt + T 打开终端

1. 设置数字签名

sudo apt-key adv --keyserver keyserver.ubuntu.com --recv-keys 3B4FE6ACC0B21F32

2. 更新下载源

sudo sed -i "s@http://.*archive.ubuntu.com@https://mirrors.tuna.tsinghua.edu.cn@g" /etc/apt/sources.list
sudo sed -i "s@http://.*security.ubuntu.com@https://mirrors.tuna.tsinghua.edu.cn@g" /etc/apt/sources.list

3. 开始更新源信息

sudo add-apt-repository "deb http://security.ubuntu.com/ubuntu xenial-security main"
sudo apt update

4. 替换Ununtu自带的vim命令(自带的有问题)

## 先卸载vim命令(操作上下左右键时，打印的是ABCD)
sudo apt-get remove vim-common## 下载新的vim命令
sudo apt-get install vim

设置root账户密码

使用快捷键 Ctrl + Alt + T 打开终端

默认root是没有密码的，直接使用 sudo su 就可以切换root账户；为了安全性可以设置密码

sudo passwd root
## 输入两次一致的密码就可以了

安装Rust环境

先安装curl命令

sudo apt install curl

 

sudo curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh

 下载完成后，尝试使用 rustc --version 命令查看rust版本 ( 有魔法的话可以下载快点 )

安装 Visual Studio Code（VSCode）

安装传输安全层（Transport Layer Security, TLS）软件包

sudo apt install apt-transport-https ca-certificates curl software-properties-common

导入微软GPG密钥

curl -sSL https://packages.microsoft.com/keys/microsoft.asc | sudo gpg --dearmor -o /usr/share/keyrings/packages.microsoft.gpg

添加VSCode仓库

将 Visual Studio Code 的存储库添加到系统中

echo "deb [arch=amd64 signed-by=/usr/share/keyrings/packages.microsoft.gpg] https://packages.microsoft.com/repos/code stable main" | sudo tee /etc/apt/sources.list.d/vscode.list

更新系统软件包列表

#打开终端，并执行以下命令来更新您的系统软件包列表：
sudo apt update

安装VSCode

sudo apt install code

启动VSCode

# 直接在终端输入
code

配置Rust插件工具