本文首发于 [QOJ](https://qoj.ac/blog/skip2004/blog/866)
大家好,我是钱哥,我来写一下 PKUSC2024 最短路径 的题解。没有做过这个题的同学可以先自行做一做。
我们下面来讲解一下如何一步步解决这个题目。
subtask 4
首先,我们来解决第一个具有挑战性的子任务:\(m \leq 2.5 n\),这个点具有一个比较显然的性质,点的度数不大。
大家来发挥一下想象力,由一个点 \(s\) 为根最短路树,几乎是以指数级展开的,因此,我们可以联想到我们普及组就学习过的算法:折半搜索。
在这个题上,我们可以执行双向 dijkstra,由 \(s\) 与 \(t\) 分别开始 dijkstra(当然,\(t\) 在反图上跑)。
当两个点的 dijkstra 相遇了,我们找到了最短路吗?很可惜,并没有。
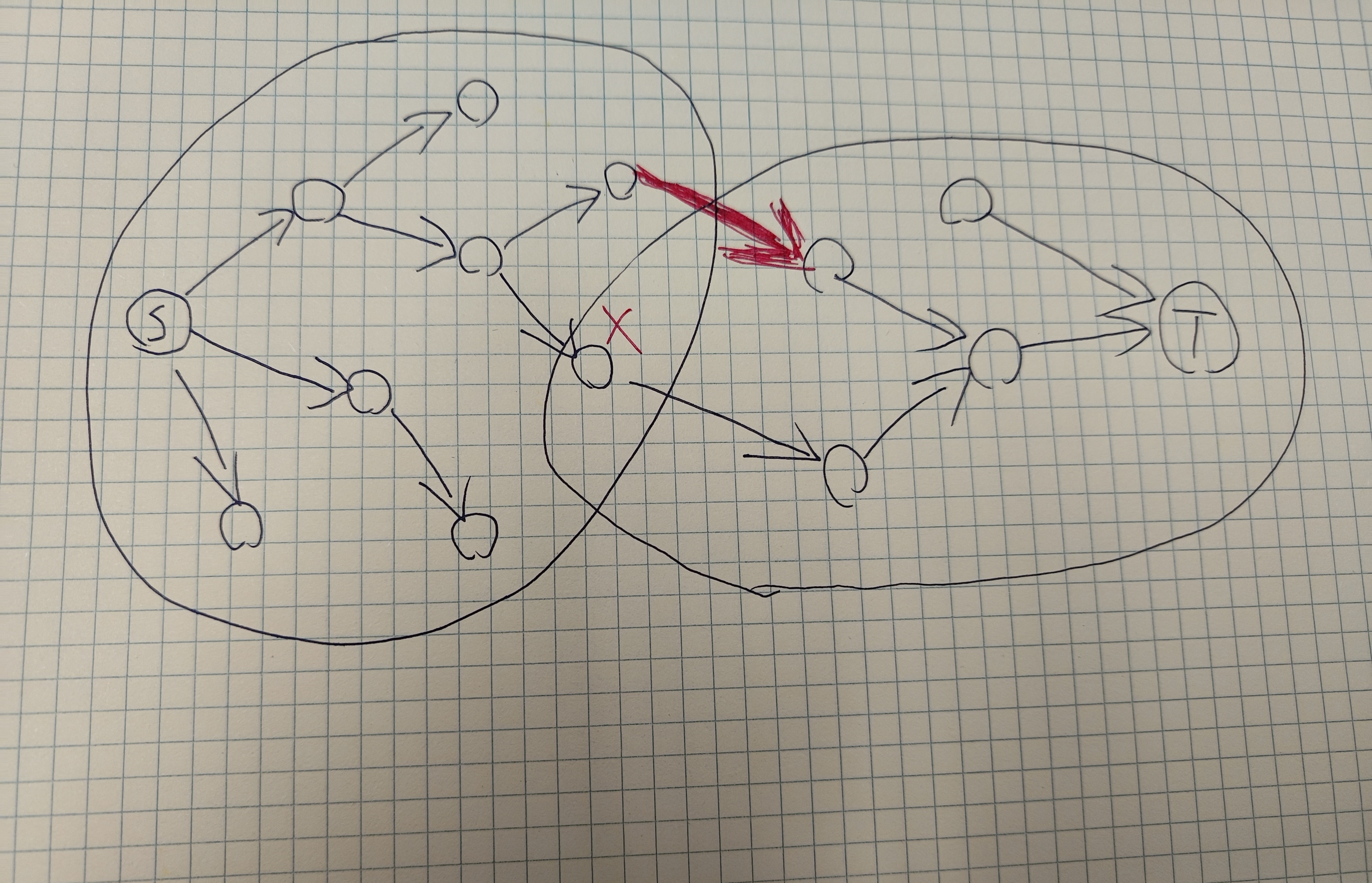
我们发现,即使两边的 dijkstra 相遇在了 \(x\),经过红色边的路径依旧可能是最短路径。
好在,我们简单分析一下,我们可以发现两边相遇过后,最多有一条不在最短路上的边。因此,我们可以枚举一侧的点,枚举它的出边,找到所有可能的路径。
现在我们来分析一下我们算法的复杂度,假设我们双向 dijkstra 一共访问了 \(S\) 个点,如果所有点度数比较平均,那么它们度数都是 \(O(m/n)\) 的,那么经过不严谨的猜测,我们整个算法的复杂度为:\(O(S * m/n + S \log S)\),其中前者是我们 dijkstra 需要松弛的边数(也是我们枚举红色边的条数),后者是堆。
那么问题来了,\(S\) 可以控制到多大呢?
双向 dijkstra
我们来分析一下 dijkstra 的行为:
q.emplace(0, S);
while (!q.empty()) {auto [d, u] = q.top(); q.pop();if (dis[u] != -1) continue;dis[u] = d;for (auto [v, w] : e[u]) {q.emplace(d + w, v);}
}
这份 dijkstra 可能和大家写法并不完全相同,但是完全可以看出是正确的 dijkstra。我们其实可以看到,每条边的目标点,事实上只有在第 \(4\) 行才第一次被用到(尽管它可能很早就在堆里了),在这之前,它完全不会影响整个代码的运行。因此,事实上每次到第 \(4\) 行时候,\(u\) 都是一个在 \([1, n]\) 中均匀独立随机生成的变量!
如果你仔细思考一下,你会发现,在双向 dijkstra 相遇之前,事实上两边也是互相独立的。因此,这个过程就像生日悖论一样,如果每次扩展最短路树上点少的一侧,期望只要扩展 \(O(\sqrt{n})\) 次,我们就可以找到相遇的点。
除此之外,我们可以发现,最短路树的点之间的所有边也是 \(O(\sqrt{n})\) 条(事实上,每次一个元素出堆就对应了一条边,而不是一个点)。
让我们回到 subtask 4,我们可以发现,此时这个算法的时间复杂度大约为 \(O(\sqrt{n} \log{n})\),这足以让我们通过这个子任务。
subtask 2
相信你发现了,上面的算法甚至没有办法通过子任务 \(2\)。虽然这个子任务是给大家各显神通的,但是如果你仔细思考,你就会发现度数在整个题目的影响是非常大的。下面我们来介绍,如何处理 dijkstra 中,每个点度数很大,导致松弛边过多。
如果你做过 \(k\) 短路,或者类似的题,它们都有用到这个技巧:我们注意到由一个点出发的边,肯定是边权小的会先出堆,因此,如果我们预先将每个点的出边按照边权排序,我们可以只往堆中塞入第一条边,当第一条边出堆时候,再把第二条边塞入堆中。如此操作,堆中的边数就线性于出堆次数了,我们也就解决了这个艰难的问题。
你也许想问,到这里,我们还是没有解决枚举中间边的复杂度,事实上,这个子任务我们只要跑单向 dijkstra 就可以了(×),因为每次到的点是独立均匀随机的,因此只有期望 \(O(n)\) 次堆操作,所以复杂度为 \(O(qn\log n + m \log m)\)(如果你写了这个算法被卡常了,那我对不起你  )。
)。
最终算法
下面我们要迎接我们的最终算法了,非常精彩!
我们现在已经可以用 \(O(\sqrt{n} \log{n})\) 的期望时间跑出相遇点了,我们下面要处理如何快速找到可能的中间边的问题。
我们考虑一下这条路径:\(s \rightarrow a \color{red}{\rightarrow} b \rightarrow t\),它的距离是 \(dist_{s, a} + e_{a, b} + dist_{b, t}\),而我们知道,\(dist_{s, a} \leq dist_{s, x}, dist_{b, t} \leq dist_{x, t}\),因此,我们这条边肯定不能太长,\(e_{a, b} \leq (dist_{s, x} - dist_{s, a}) + (dist_{x, t} - dist_{a, t})\),显然,\(e_{a, b} \leq 2 \max(dist_{s, x} - dist_{s, a}, dist_{x, t} - dist_{a, t})\),我们考虑在大的一侧找这条边,假设是 \(a\) 侧,也就是我们要找到 \(a\) 所有边权 \(\leq 2 (dist_{s, x} - dist_{s, a})\) 的出边。
那么边权 \(\leq 2 (dist_{s, x} - dist_{s, a})\) 的出边多不多呢,直觉上是不多的,因为看起来就和边权 \(\leq (dist_{s, x} - dist_{s, a})\) 的出边差不了两倍嘛!后者就是最短路树内部的边,根据我们之前的说法,只有 \(O(\sqrt{n})\) 条,所以我们这么枚举边数肯定不多!
如果你只想感性理解,这里就结束了,时间复杂度为 \(O(q\sqrt{n}\log{n} + m\log{m})\)。但是严谨的来说,我们知道 \(a\) 的出边边权和 \((dist_{s, x} - dist_{s, a})\) 并不独立,我们还得证明 \(\leq 2 (dist_{s, x} - dist_{s, a})\) 的出边不多。
证明
定理:我们有至少 \(1-O(n^{5})\) 的概率,对于任意 \(a, v\),记 \(A\) 为 \(a\) 出边边权 \(\leq v\) 的边数,\(B\) 为 \(\leq 2v\) 的边数,我们有:\(B < 64\log n + 4A\)。
证明:
对于一对固定的 \((a, v)\),我们先掏出 \(a\) 所有边权 \(\leq 2v\) 的出边,一共有 \(B\) 条,在这个前提下,每条边有 \(\frac{1}{2}\) 的概率边权 \(\leq v\),且独立。
如果 \(B < 64 \log_2 n\),显然成立。不然,根据 Chernoff Bound,\(Pr[A \leq \frac{B}{4}] \leq e^{-\frac{B}{8}} \leq e^{8\log_2 n} \leq n^{-8}\),也就是说几乎一定成立。
根据 Union Bound,我们可以得知,所有 \((a, v)\) 成立的概率至少有 \(1 - n^{-8} \times n \times V\),至于怎么把 \(V\) 去掉,我懒得写了。
这个证明多带了一个 \(\log\),确实不太优美,但是并不影响时间复杂度,当然,实测一下还是比较像 \(O(\sqrt{n})\) 的。