题目链接:
来自罗勇军《算法竞赛》书中的习题。
题意:给长度为 \(N\) 的数组和一个整数 \(S\),求总和不小于 \(S\) 的连续子序列的最小长度。
方法一:尺取法
主要思想为:当 \(a_1, a_2 , a_3\) 满足和 \(\geqslant S\),得到一个区间长度 \(3\), 那么去掉开头 \(a_1\),剩下 \(a_2,a_3\), 是否满足 \(\geqslant S\),如果满足,那么区间长度更新,如果不满足,那么尾部向后拓展,判断 \(a_2,a_3,a_4\) 是否满足条件。重复这样的操作。
主要分为四步:
- 如果 \(\rm sum<S\),就不断的放大 \(\rm right\),直到 \(\rm sum \geqslant S\) 或者 \(\rm right>N\)
- 如果第 \(1\) 步循环结束,\(sum<S\),程序结束,不走到 \(3\)
- 满足 \(\rm sum \geqslant S\),更新 \(\rm res=min(res,right-left)\)
- 放大 \(\rm left\) 回到 \(1\)
时间复杂度为 \(O(n)\).
\(\rm eg.\)
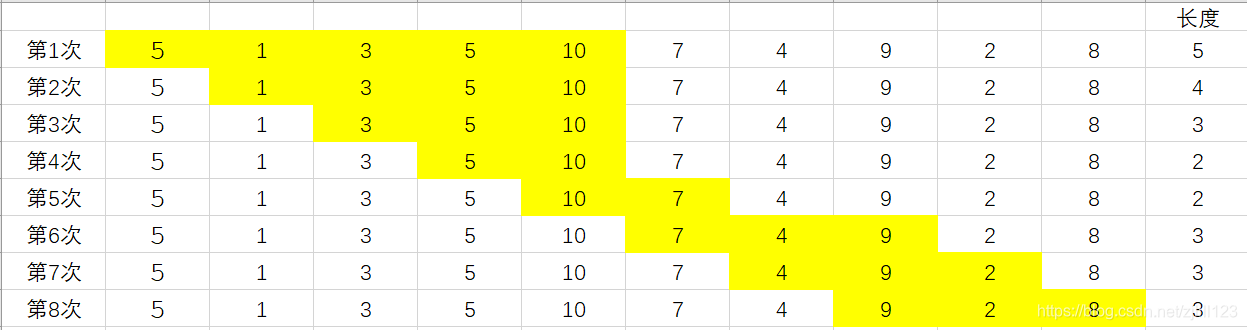
\(\rm ans=2\).
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int s[100005];void solve() {int N, S;cin >> N >> S;for (int i = 1; i <= N; i++) {cin >> s[i];}int l = 1, r = 1, sum = 0, ans = N + 1;while (l <= r) {while (r <= N && sum < S) sum += s[r++];if (sum < S) break;ans = min(ans, r - l);sum -= s[l++];}if (ans == N + 1) cout << 0 << "\n";else cout << ans << "\n";
}int main()
{int t = 1;cin >> t;while (t--) solve();return 0;
}
方法二、前缀和+二分
如果想要求出序列中某个连续子序列的和,我们可以采用前缀和的方式求出。得到前缀和之后,我们可以采取双循环枚举的方式枚举序列的所有子区间,从而得出合适的区间长度。但由于本题数据范围为 \(O(10^5)\),显然这样会超时。
for(int i = 1; i <= n; i ++) {for(int j = i; j <= n; j ++ ){if(sum[j] - sum[i - 1] >= s) {ans = min(ans,j - i + 1);break;} }
}
分析第二重循环可以发现,我们只需要找到第一个满足 \(\rm sum[j] - sum[i - 1] \geqslant s\) 的就可以直接 \(\rm break\) 了,但是我们需要去枚举每一个 \(\rm sum[j]\),比较浪费时间,可以发现, \(\rm sum[x]\) 是一个递增的序列,这时候我们就可以采取二分的策略,寻找到第一个满足 \(\rm sum[j] - sum[i - 1] \geqslant s\) 的 \(j\)。时间复杂度为 \(O(nlogn)\).
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>#define INF 0x3f3f3f3fusing namespace std;const int maxn = 1e5 + 10;typedef long long LL;LL sum[maxn], a[maxn];int t, n, s; int main() {cin >> t;while(t --) {memset(sum,0,sizeof(sum));cin >> n >> s;for(int i = 1; i <= n; i ++) {cin >> a[i];// 前缀和 sum[i] = sum[i - 1] + a[i];}// 特判,如果整个序列和 < s,则一定没有合适的区间 if(sum[n] < s) puts("0");else {int ans = INF;for(int i = 1; i <= n; i ++) {int l = i;// 后面的判断没有意义,可以直接跳出循环 if(sum[n] - sum[l - 1] < s) break;int r = n;// 二分查找最小的右端点满足 sum[mid] - sum[i - 1] >= s while(l < r) {int mid = l + r >> 1;if(sum[mid] - sum[i - 1] < s) l = mid + 1;else r = mid;}// 寻找到最小的区间 ans = min(ans,r - i + 1);}cout << ans<< endl;}}return 0;
}
参考文献:poj3061:Subsequence(最短子序列和) -- 前缀和与二分