总算给我看懂到底是什么意思了。。。
首先我们来考虑按照时间+扫描线进行处理,假设操作如下
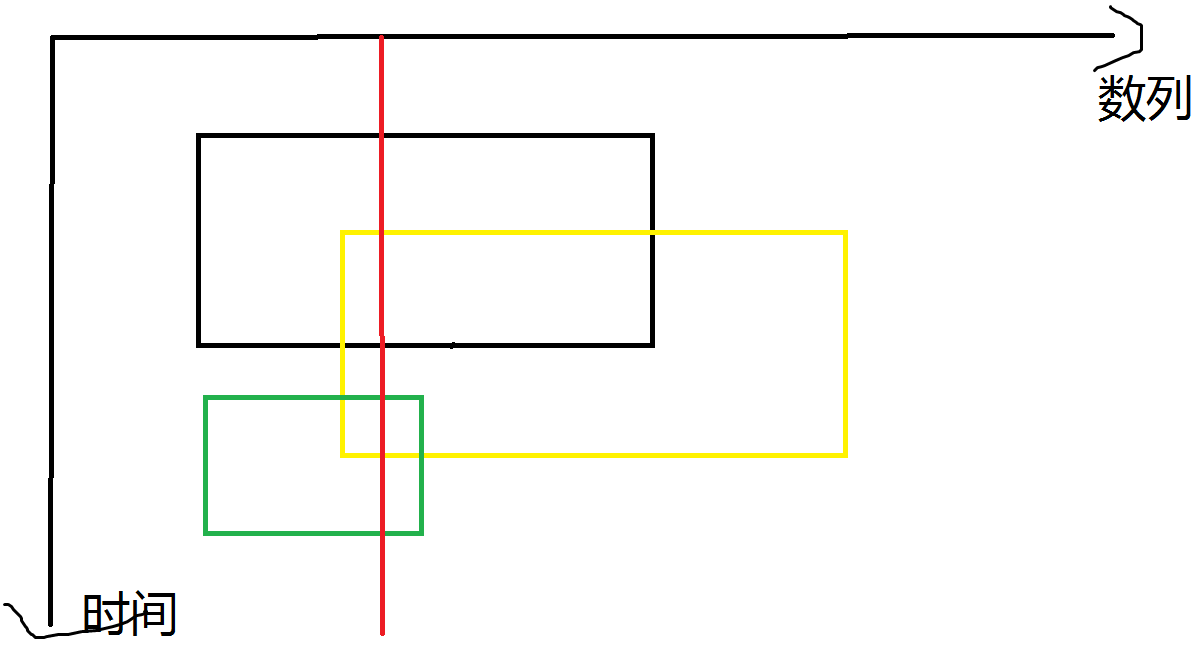
黑色是加操作,黄色是乘操作,绿色是加操作,对于红色那条线所代表的点,随着时间的流逝,首先在刚刚进入黑色的时候,这一点的值就被加上了一个数,然后刚刚进入黄色的时候,这一点的值就被乘上了一个数,刚刚进入绿色的时候,这一点的值就被加上了一个数,所以总体顺序是加乘加,然而如果我们按照扫描线处理,顺序就会变成黑绿黄,就错了
所以这道题目的顺序是很重要的,这启示我们不能按照扫描线做,只能老老实实按照时间递增去做
假设没有撤销操作,那么这就是普通的线段树了
有了撤销操作肯定要做一些更改,而且还有时间这一维度,由于我们不能按照扫描线做,我们就对时间进行分块处理
接下来仍然先讨论没有撤销操作的做法
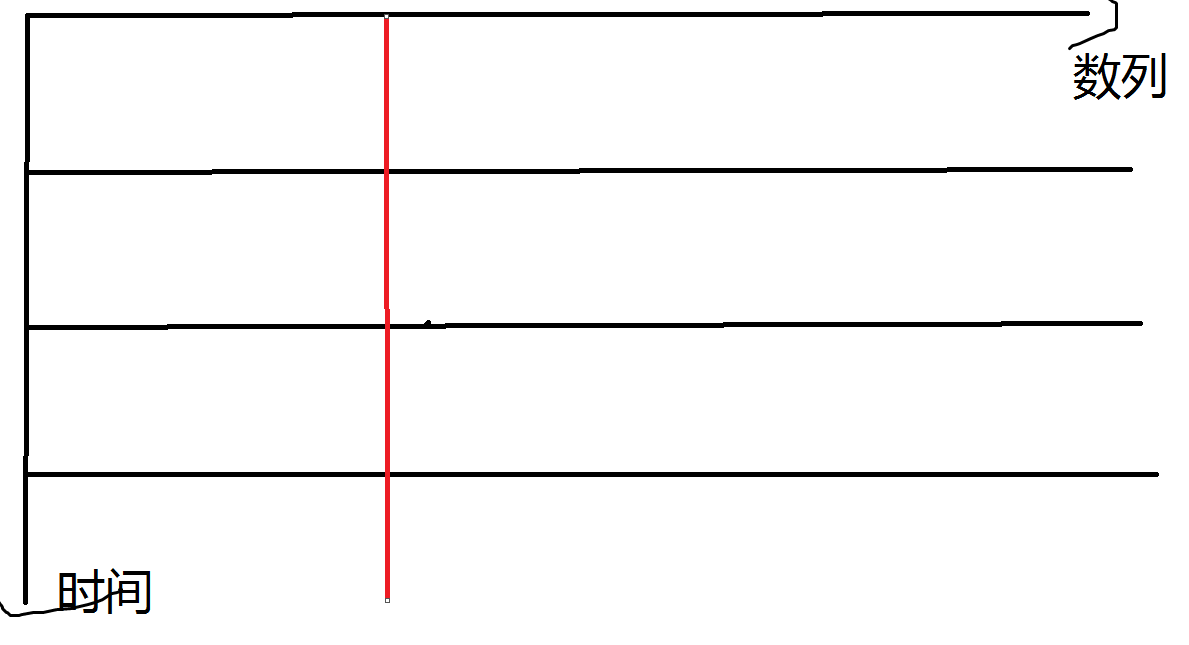
我们仍然值来看红色这个点,假设经过第一块之后,他的值为\(x\),那么接下来我们考虑经过第二块之后他会变成什么
遇到了加操作,变成了\(x+b_1\);遇到了加操作,变成了\(x+b_1+b_2\);遇到了乘操作,变成了\((x+b_1+b_2)\times a_1=a_1x+a_1b_1+a_1b_2\);遇到了加操作,变成了\(a_1x+a_1b_1+a_1b_2+b_3\);遇到了乘操作,变成了\((a_1x+a_1b_1+a_1b_2+b_3)\times a_2=a_1a_2x+a_1a_2b_1+a_1a_2b_2+a_2b_3\)
根据以上过程我们不难发现,我们可以考虑每个加操作的贡献,一个加操作的贡献就是这个加的值与其后面所有乘操作的积,而最开始的值\(x\),最后也会乘以这个块里面所有乘操作的积;以上两部分加起来就是\(x\)经过这个块之后会变成的值
于是我们可以对每一个块内都维护一个线段树,线段树的每一个叶子节点维护两个值,\(a\)和\(b\),表示叶子节点所代表的位置传入这个块的值为\(x\),那么经过这个块之后,\(x\)就会变成\(ax+b\)。显然\(a,b\)这两个参数只跟这个块里面的修改操作有关,跟\(x\)无关,所以上述维护是没有问题的
然后我们再来考虑撤销操作。有了撤销操作,就是将一个无限长的矩形变成了一个有限长度的矩形,就像这样
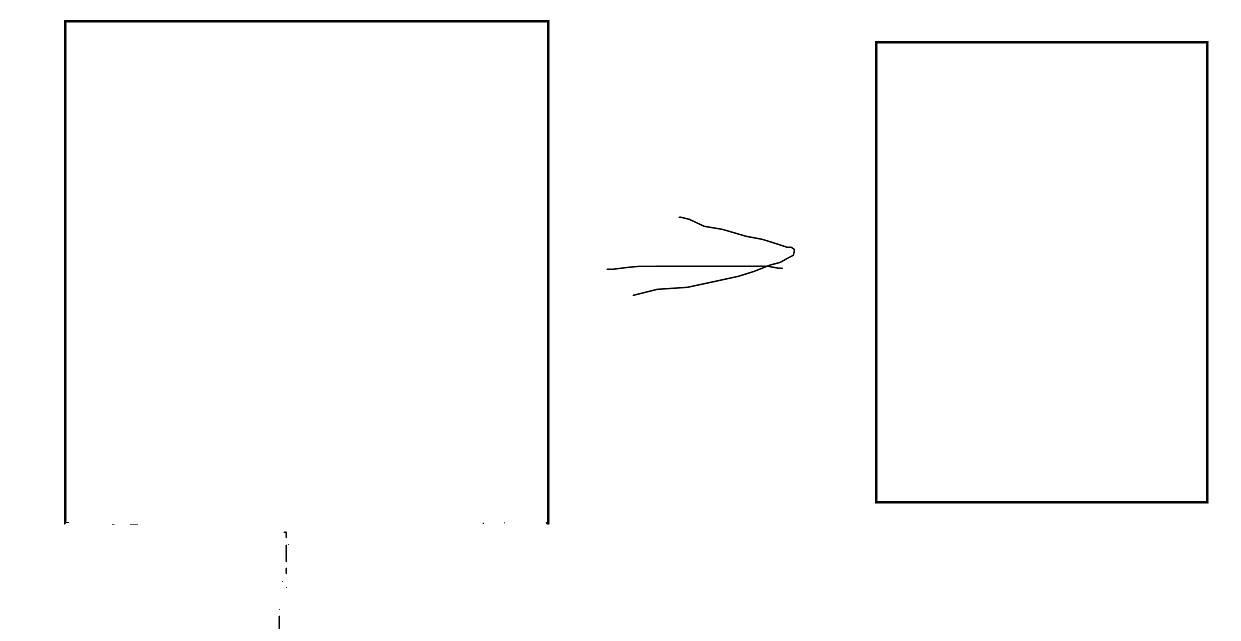
也就是代表这个操作的有限区间
我们假设这个矩形上面的边所在的块的编号为\(l\),下面的边所在的块的编号为\(r\),对于\([l+1,r-1]\)的块的线段树来说,是否有这个操作,任意一个线段树的任意一个叶子节点维护的\(a,b\)是不会变化的,所以我们只需要暴力修改\(l\)的线段树就好了,而且在处理\(r\)的线段树的时候,不用管这个操作
查询的时候,前面的块的部分利用线段树快速查询,块内部分暴力查询即可





![[SWPUCTF 2016]Web7 利用ssrf攻击redis](https://img2024.cnblogs.com/blog/3428431/202405/3428431-20240518154640760-1864723604.png)