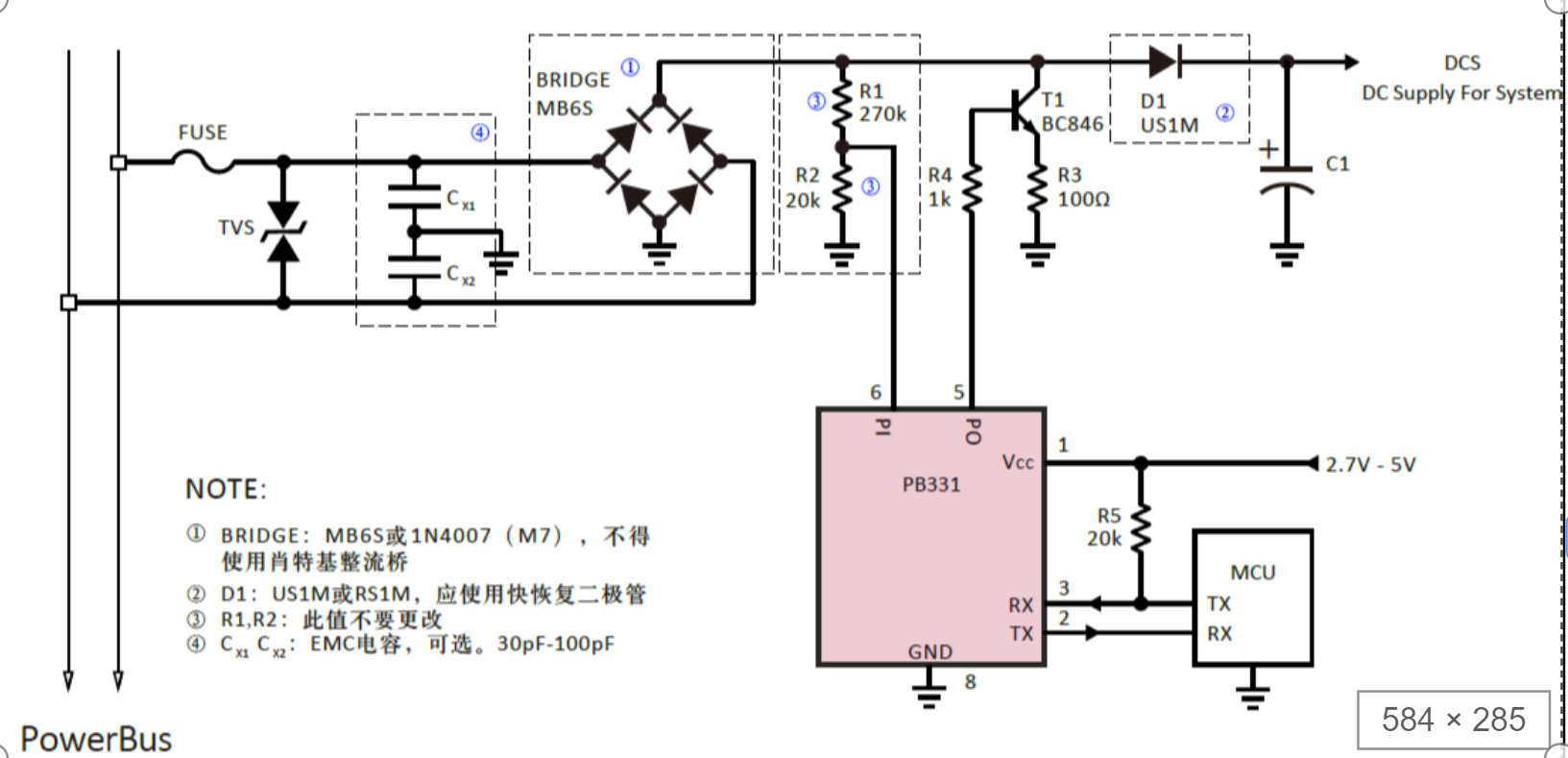
存钱计划(三)
时间限制(普通/Java):1000MS/30000MS 内存限制:65536KByte
描述
TZC的店铺比较多,上次WY随便走只要能走到就行,现在他学聪明了。WY去买东西的话,确定一家店以后,当然他先要想想怎么样走到那家店走的路最少。店与店之间是有走的方向的,从店A到店B可以,店B到店A未必可以。店与店之间是有一定距离的。
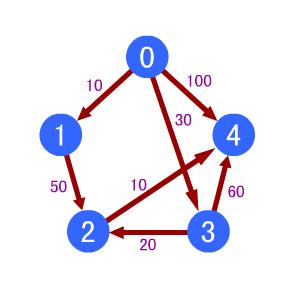
上面就是路线,为方便起见,店铺都用数字表示,0表示WY的起点,店与店之间以及起点与店距离用d表示。WY从0开始到4店铺 那么最短路线为0-->3-->2-->4 总长为 60。
如果从0店铺开始到1店铺最短路线只有0-->1 总长 10。
当然也有可能没有路的情况。
输入
输入有多组测试数据。
每组数据的第一行为整数n(n<=10),表示店铺总数。所有店铺的编号为0~n-1。
接下来有若干行,每行为3个整数
a b t
表示a编号的店铺走向b编号的店铺之间的一条路径,长度为t。0<=a,b<n(为有向路径,不能反向行走)。
当a b t的值为0 0 0 表示店铺之间的路径输入完毕,不做任何处理。
最后一行输入店铺的编号k(k<n)
输入n为0时表示结束程序。
输出
输出从店铺0到k店铺的最短路线的长度。如果没有路的话,输出 NO WAY!
样例输入
5
0 1 10
0 3 30
0 4 100
1 2 50
2 4 10
3 2 20
3 4 60
0 0 0
4
5
0 1 10
2 0 50
0 3 10
0 0 0
2
0
样例输出
60
NO WAY!
提示
简单最短路径问题
采用Dijkstra算法;
每次选择离A(初始开始的那个点)最近的那个点,然后更新就好啦。
算法代码:
点击查看代码
void dijkstra(){int i,j;for(i=0;i<nj;i++)//nj就是多少个店 dis[i]=INF;//全部初始化为最大; dis[0]=0; //还没开始,先初始化为0; memset(visited,0,sizeof(visited));//来记录是否遍历过该点; for(i=0;i<nj;i++){int mark=-1,mind=INF;//mind 来记录最小的值,最优的解; for(j=0;j<nj;j++){if(!visited[j]&&dis[j]<mind)//最开始一定是第一个点 起点{mind=dis[j];mark=j;}}if(mark==-1)//全部遍历完了 break;visited[mark]=1;//记录该点,变成1吧! for(j=0;j<nj;j++){if(!visited[j]&&dis[mark]!=INF&&mp[mark][j]!=INF)//该点是否遍历过&&该点值不是无穷大&&图上对应的也不是无穷大,这边意思是mp图上还没更新带dis上所以也判断一下; {dis[j]=min(dis[j],dis[mark]+mp[mark][j]);//找到最小,最优化的,更新dis表! }}}
}