20240520刷题总结

T1(状态置换，搜索与dp, dp存值结构体)

T376。
还是从搜索角度去考虑：时间，前i物品，最多拿多少。
这样我们去设计状态，我一开始设置：时间，前i，值是拿多少。会发现这样会爆。
其实换一下，优化效果更好。前i物品，最多拿j，用的最少时间。
实际转移就是背包。存值就存结构体。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>using namespace std;const int N = 2010, INF = 0x3f3f3f3f;struct Node
{int day, tim;bool operator< (const Node& W) const{if (day != W.day) return day < W.day;return tim < W.tim;}
}f[N];
int n, t, m;Node add(Node a, int b)
{if (b > t) return {INF, INF}; //一天都放不下Node c = {a.day, a.tim + b};if (c.tim > t) c.day ++ , c.tim = b;return c;
}int main()
{scanf("%d%d%d", &n, &t, &m);for (int i = 1; i <= n; i ++ ) f[i] = {INF, INF};f[0] = {1, 0}; //第1天for (int i = 1; i <= n; i ++ ){int v;scanf("%d", &v);for (int j = i; j; j -- ){f[j] = min(f[j], add(f[j - 1], v));}}for (int i = n; i; i -- ){if (f[i].tim <= t && f[i].day <= m){printf("%d\n", i);return 0;}}puts("0");return 0;
}

T2(数学题）

s->t, 首先构造方案。先往下走，走到不能走乘2，一直加，加到不能加乘，乘完减回来。

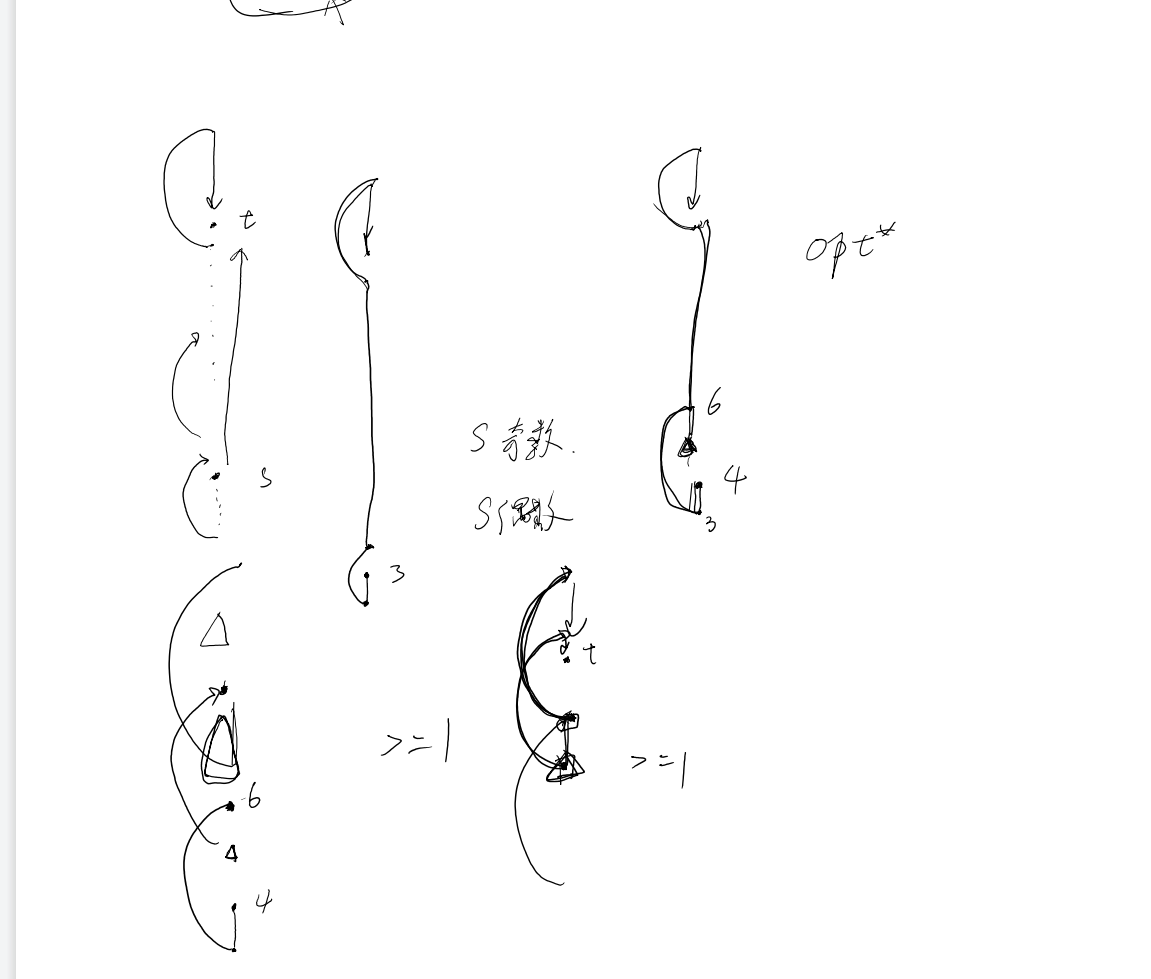
唯一有疑问的是乘完往不往下走1。假设乘完往下走，乘二至少剩下1个格。

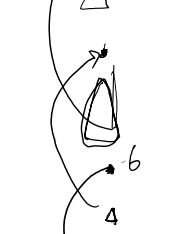
中间大于等于一，因为最坏情况也是偶数。如果起点为奇数，那么数为2* （n - 1)， 减n，是n - 2， 而n是严格>=2的。所以最起码不会更坏。
也就是1 + 1 <= (>=1) + 1
这样就行了。最后跳直接枚举就行了。 k * 2 - n + 1, (k + m) * 2 - n + m。其实也一样。

#include <bits/stdc++.h>
using namespace std;int n, k, ans = 0;int main() {cin >> n >> k;if (n >= k)ans = n-k;else {int i=n, step=0;for (;i<k;) {pif (i * 2 > k)ans = max(ans, step + 1 + i*2-k);i++;if (i % 2 == 0 && i/2 < n)step = max(step+1, n-i/2 + 1);elsestep = step+1;}ans = max(ans, step);}cout << ans;return 0;
}

T3：（回文，重新分类，dp套小dp，两个相互加中间中转）
首先回文问题，从中间或两端走，这里从中间bfs。其实这个好想。

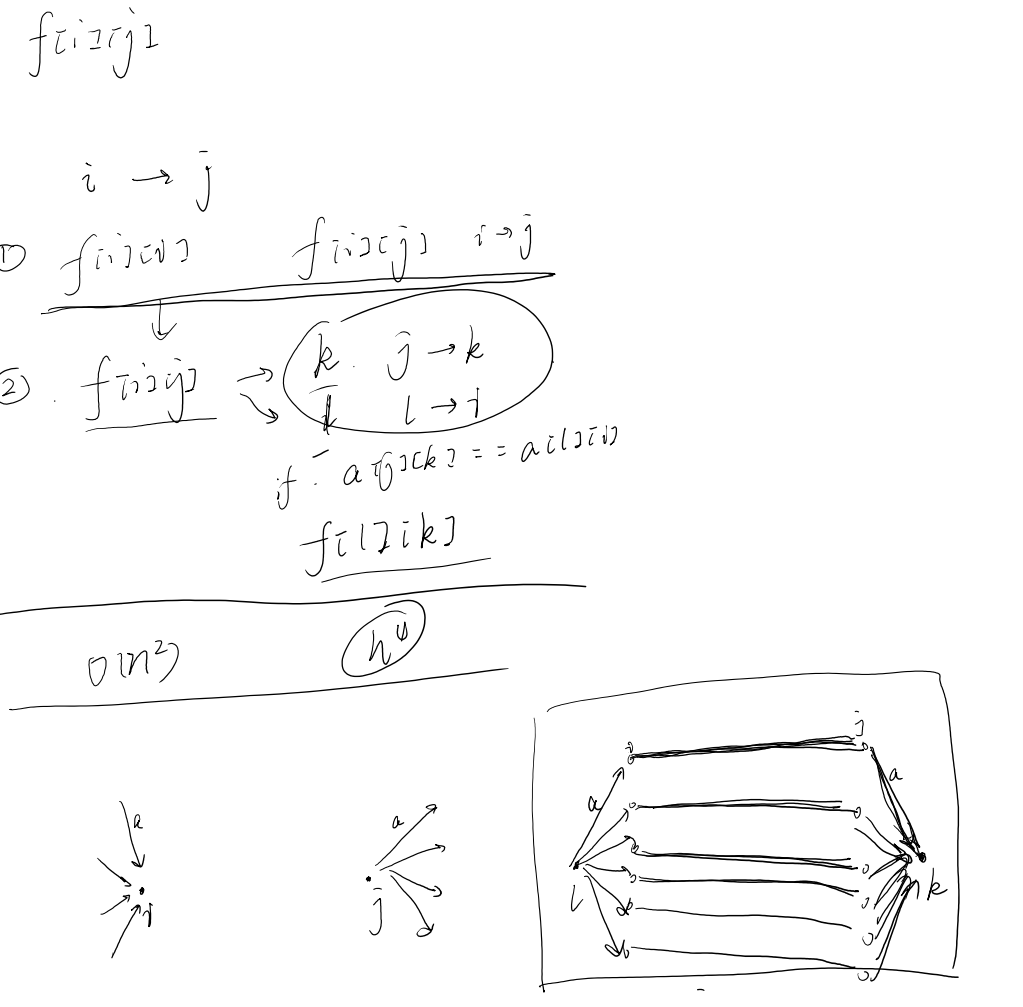
每次扩展相同字母。
其实极端情况能卡爆。就是每个都是a扩展。
这样就过不去了。考虑优化。这里两个相互加，我们可以考虑在中间加一个中转，这样不就行了？如何套呢？先扩展一条边的状态就行了，再扩展。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>using namespace std;const int N = 410, M = 30, K = 60010;int h[N], pre_h[N], e[K << 1], ne[K << 1], w[K << 1], idx;bool flag[N][N];
int f[N][N], g[N][N][M];
int c[N];
struct Node
{int x, y, c;
}q[5000010];
int n, m;void add(int h[], int a, int b, int c)
{e[ ++ idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx;
}void bfs()
{memset(f, 0x3f, sizeof f);memset(g, 0x3f, sizeof g);int hh = 0, tt = -1;for (int i = 1; i <= n; i ++ ) q[ ++ tt] = {i, i, 0}, f[i][i] = 0;for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )if (i != j && flag[i][j]) q[ ++ tt] = {i, j, 0}, f[i][j] = 1;while (hh <= tt){Node t = q[hh ++ ];if (!t.c) //f{for (int i = h[t.y]; i; i = ne[i]){int j = e[i];if (g[t.x][j][w[i]] > f[t.x][t.y] + 1){g[t.x][j][w[i]] = f[t.x][t.y] + 1;q[ ++ tt] = {t.x, j, w[i]};}}}else{for (int i = pre_h[t.x]; i; i = ne[i]){int j = e[i];if (t.c != w[i]) continue;if (f[j][t.y] > g[t.x][t.y][t.c] + 1){f[j][t.y] = g[t.x][t.y][t.c] + 1;q[ ++ tt] = {j, t.y, 0};}}}}
}int main()
{scanf("%d%d", &n, &m);while (m -- ){int a, b;char c;scanf("%d %d %c", &a, &b, &c);flag[a][b] = true; //单向边add(h, a, b, (int)c - 'a' + 1), add(pre_h, b, a, (int)c - 'a' + 1);}bfs();int k;scanf("%d", &k);for (int i = 0; i < k; i ++ ){scanf("%d", &c[i]);if (i){if (f[c[i - 1]][c[i]] < 1e9) printf("%d\n", f[c[i - 1]][c[i]]);else puts("-1");}}return 0;
}

T4（枚举，spfa要快一些)

枚举最短路上边边，跑最短路。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>using namespace std;const int N = 1010, M = N * N;int h[N], e[M], ne[M], w[M], idx;
int pre[N], prew[N];
bool st[N];
int d[N];
int n, m;
bool flag;
void add(int a, int b, int c)
{e[ ++ idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx;
}void spfa(int del)
{queue<int> q;flag = false;memset(d, 0x3f, sizeof d);d[1] = 0;q.push(1);while (q.size()){int t = q.front(); q.pop();st[t] = false;for (int i = h[t]; i; i = ne[i]){int j = e[i];if (i == del) continue;if (d[j] > d[t] + w[i]){pre[j] = t;prew[j] = i;d[j] = d[t] + w[i];if (!st[j]) q.push(j), st[j] = true;}}}
}int main()
{scanf("%d%d", &n, &m);while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);}spfa(0);int ans = d[n];int k = n, w = prew[n];while (k){spfa(w);w = prew[k];k = pre[k];ans = max(ans, d[n]);}cout << ans << endl;return 0;
}