北京端午游
1、奥林匹克森林公园
🅿️交通:
🚇地铁8号线森林公园南门站出
🚗开车不推荐,游园还得回起点拿车,有点绕不值当
🕙时间:半天or全天,根据路线决定
🍚餐饮:自带或出国奥村门吃,太多好吃的,推荐日坛涮肉,眉州和满久居
奥森北园北门出来有个林奥city!里面有好多新开的店!
🆓免费游玩路线:
南门进-西门出回家
南门进-国奥村门出,去路两边的饭店吃晚饭回家
西门进-南门出,出门右转进亚洲金融大厦玩,再去国奥村吃饭回家
4️⃣ #中国工艺美术馆
⚱️ 国家级审美!咖啡&文创&邮局
🚶♀️ 步行约30m
🎫 中国工美馆中国非遗馆👸号免费预约,特展60r
📆 周二至周日9:00-17:00,约3h
5️⃣ 新奥购物中心&新奥天虹
🍦 两个商场近,面积大
🚶♀️ 步行约500m
🍧 小吊梨汤、唐肴长安小馆、东来顺、云海肴
📆 10:00-22:00,约3h
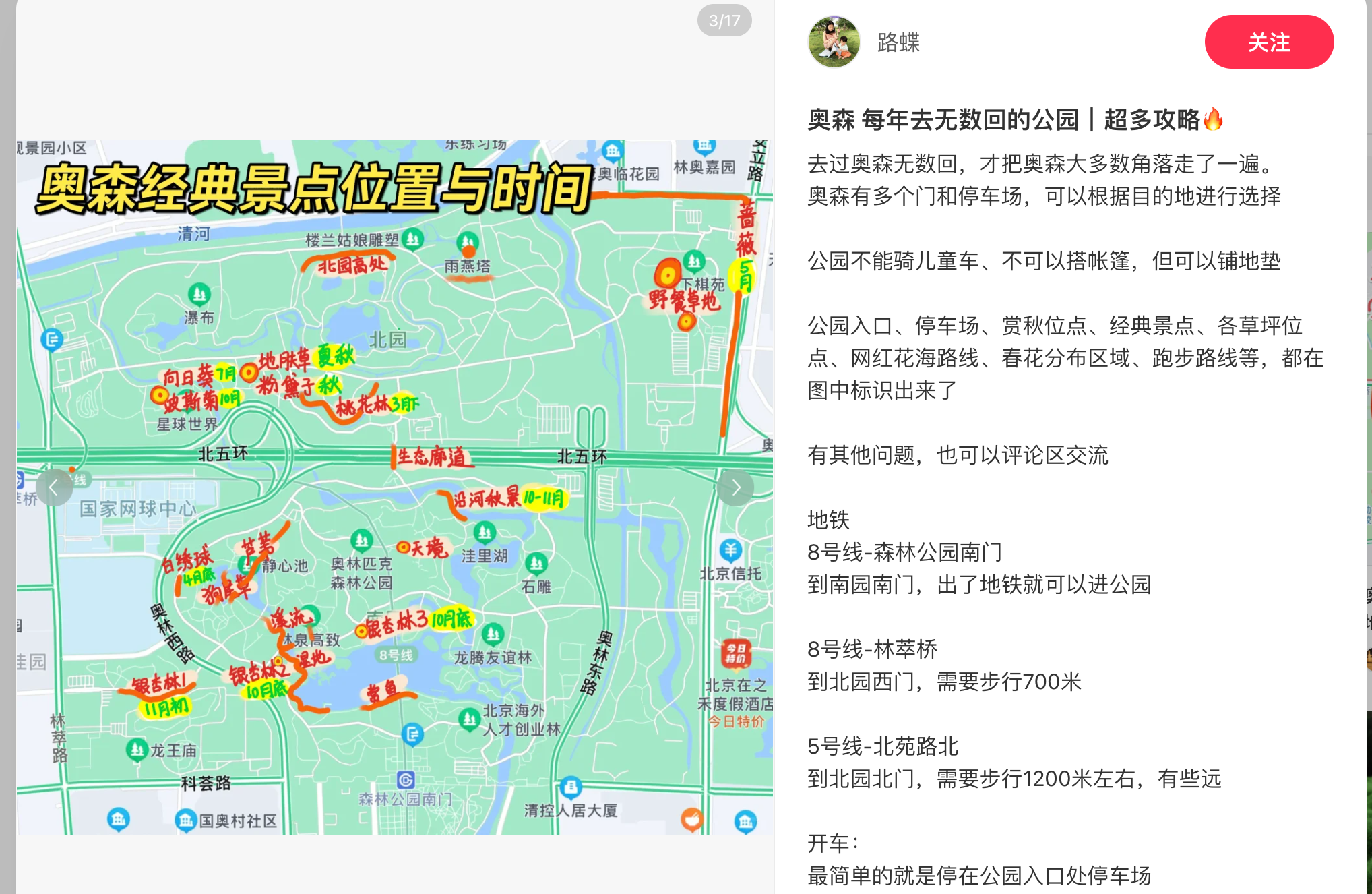
白绣球

粉黛子

蔷薇花墙

鹿营

地肤草