Tips: 作者想题的时候在打块,可能是错的。
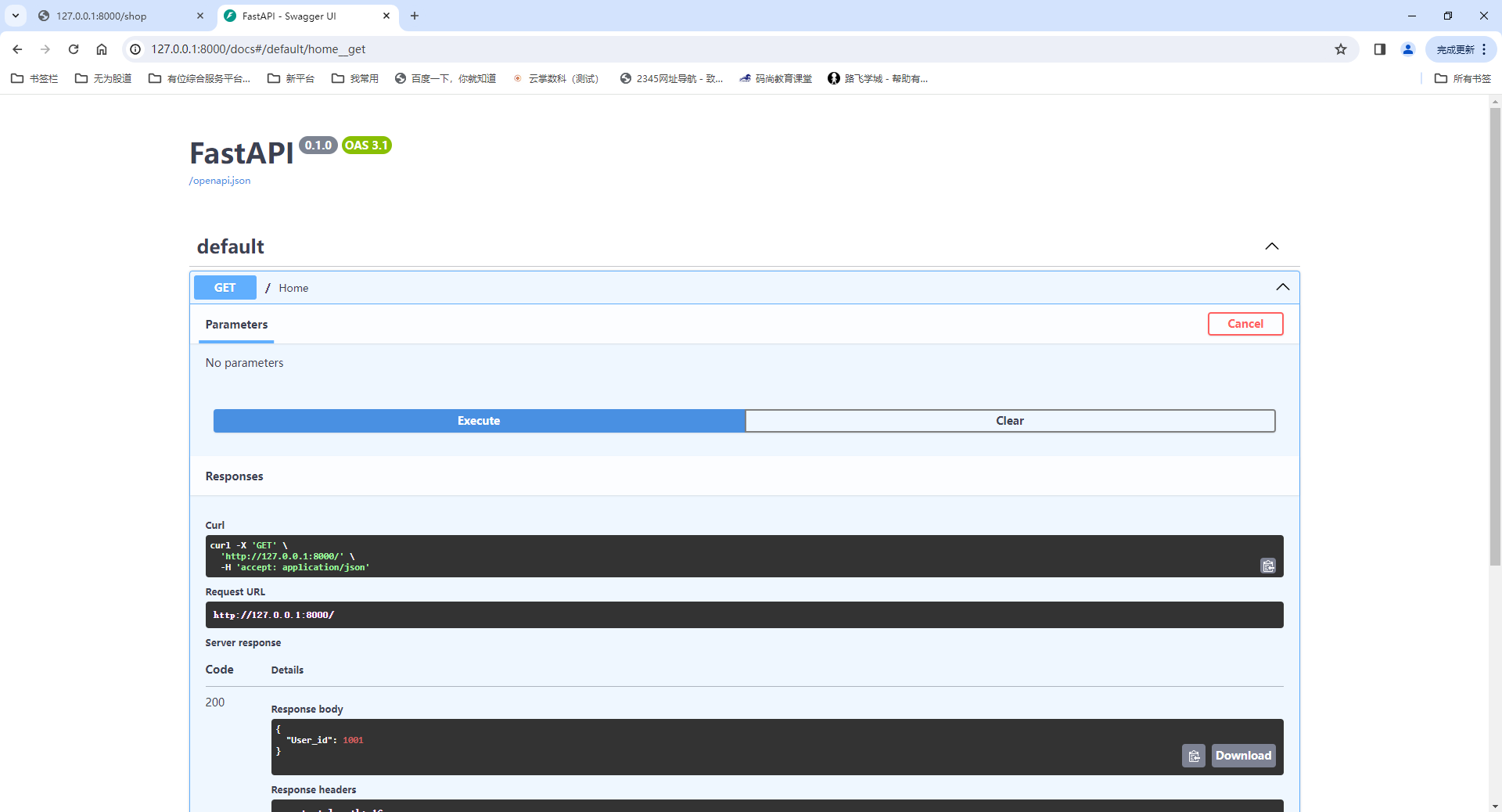
题目长这样:

首先这个 \(a\) 没有任何用,只关注下标。
(1) 是超级原神题,答案是(1,6), (1,2), (5,6)。
(2) 我们拿 \(m = 3\) 玩一下:
1 (2) 3 4 5 6 7 8 9 10 11 12 (13) 14
1 4 7 10
3 6 9 12
5 8 11 14
做完了。
然后 \(m > 3\) 的时候,后面就四个四个分就行。
(3)
感觉这个我只要找到足够多的合法解就行了啊,尽量多找找长啥样的解是合法的就行,不过出题人把上界卡得很紧的话那感觉有点没救。
考虑到 (2) 给了一个比较厉害的解,我们考虑他长啥样:
我们把序列四个分为一组,编号 \(0, 1, 2, \cdots , m\) (最后一组2个)
发现 \((2, 13)\) 对应的就是一组的第二个和另一组的第一个。这启发我们将他写成 \((4i + 2, 4j + 1)\) 的形式,注意到:
- \(i, j\) 向左右平移相同步都合法,这是显然的。
- 注意到 \((2, 9)\) 也是合法的。构造方式如下:
1 2 3 4 5 6 7 8 9 10 ...
1 3 5 7
4 6 8 10
...
-
我现在有形如 \((4i + 2, 4j + 1)\) 的一组合法解 \((x, y)\),不难发现 \([x - 1, y + 1]\) 中除了 \(x, y\) 都覆盖了。我们让 \(y \leftarrow y + 8\),那么这时候 \(y\) 就是要覆盖的,而 \(y + 1\) 等价于不用覆盖。那问题就变成了覆盖 \([y, y + 8]\) 且 \(y + 1\) 已覆盖的问题,等价于 \((y + 1, y + 8)\) 的合法性,这等价于 \((2, 9)\),是合法的,归纳一下发现 \((x, y + 8k)\) 都合法。
-
基于我前面有两组解 \((2, 9), (2, 13)\),所以形如 \((4i + 2, 4j + 1) (j \ge i + 2)\) 的都合法。解数大概是 \(\binom{m + 1}{2} - 2(m + 1)\), 可能算错了。
然后估算了一下发现不够 \(\frac{1}{8}\), 怎么会是呢。然后发现我唐了,因为有一些显然的情况:
- \((4i + 1, 4j + 2) (i \le j)\) 是肯定合法的,因为剩下的块全是连续的四个分分就行了。解数 \(\binom{m + 1}{2} + (m + 1)\),可能算错了。
加起来发现等于 \(m^2 - 1\), 那么
后面随便做一下就能证出来 \(P_m \ge \frac{1}{8}\)。
不过感觉这个在 \(m\) 比较小的时候可能有点问题,分类讨论单独证一下吧。(也许没问题?)
大概想了 20 分钟,主要是第二问给了我一些启发,然后就发现解有很强的归纳性。不过我在 \((4i + 1, 4j + 2)\) 这里唐了很久,导致解太少了做不出来,简直是弱智。
remaining problems :是否还有别的形式的解?
upd : 感觉前面的有点假。