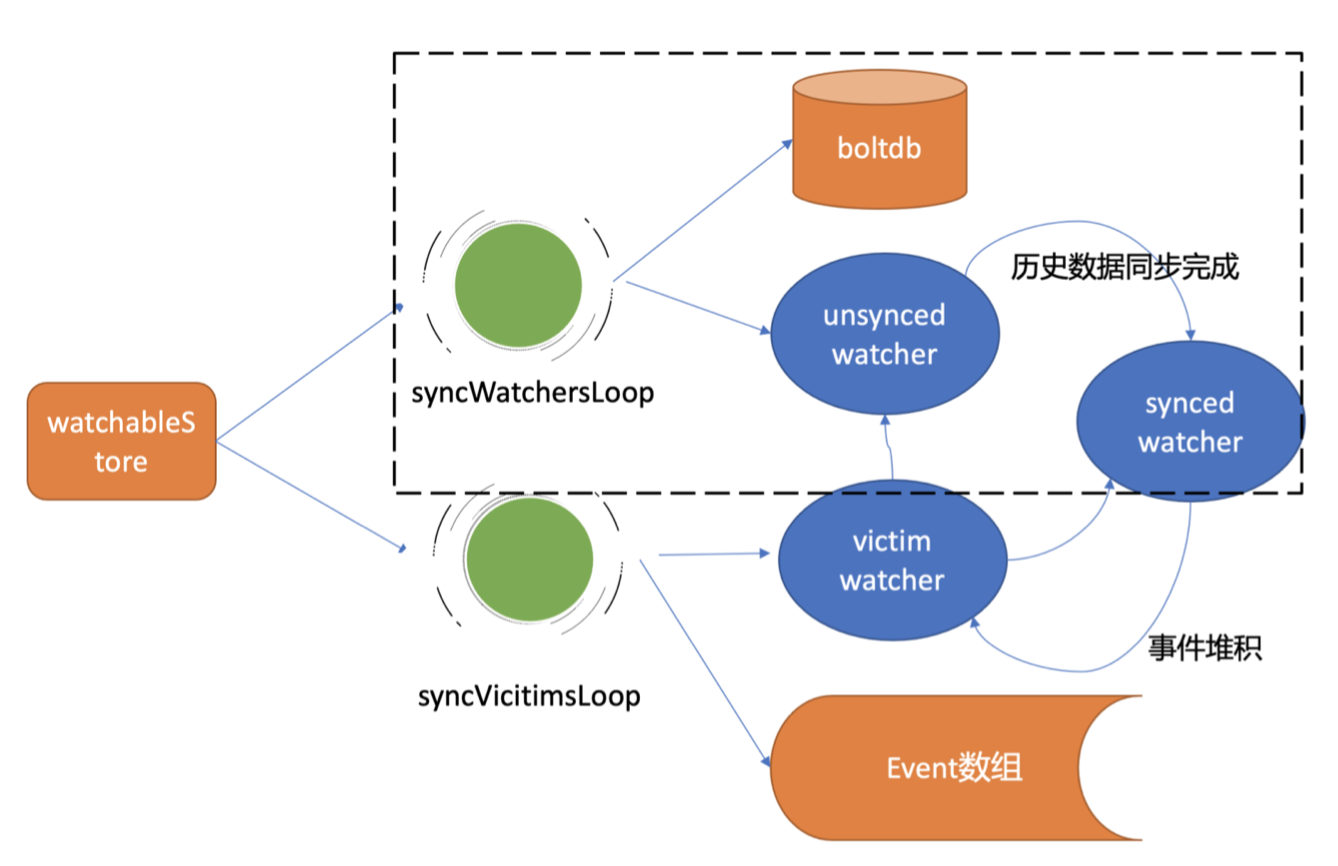
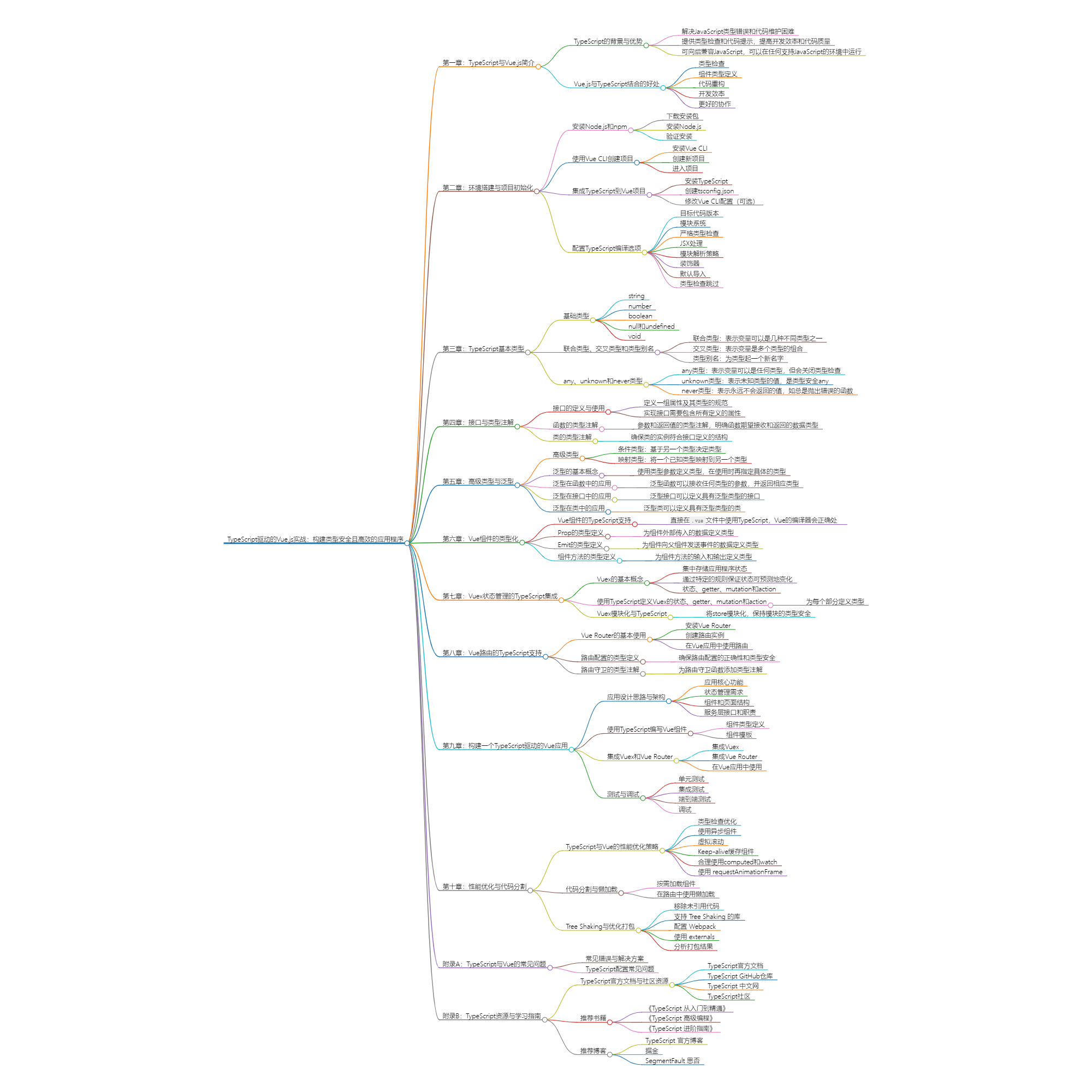
讲讲图灵对计算机的贡献
图灵机发明的背景
阿兰·马蒂森·图灵 (Alan Mathison Turing)于 1921 年出生在伦敦, 从小就表现出惊人数学和科学能力。

艾伦·麦席森·图灵(Alan Mathison Turing),1912-1954,英国数学家、计算机学家、逻辑学家、密码学家、哲学家、理论生物学家。(图片来自维基百科)
他对计算机科学的建树始于 1935 年,当时他是剑桥国王学院的硕士生,他开始解决德国数学家 大卫·希尔伯特提出的问题: Entscheidungsproblem (德语),即“可判定性问题”: 是否存在一种算法,输入正式逻辑语句,输出准确的"是"或"否"答案?
如果这样的算法存在, 可以回答比如 "是否有一个数大于所有数?" (虽然我们知道答案:没有)。但有很多其他非常难以解决的数学问题,我们想知道答案,因为如果我们知道是没有解决方法的,就不用花时间去尝试解决了。
美国数学家阿隆佐·丘奇, 于 1935 年首先提出解决方法,开发了一个叫“Lambda 算子”的数学表达系统,证明了这样的算法不存在。虽然“Lambda 算子”能表示任何计算,但它使用的数学技巧难以理解和使用。
同时在大西洋另一边,阿兰·图灵 想出了自己的办法来解决"可判定性问题",提出了一种假想的计算机,现在叫图灵机(Turing Machines),图灵机提供了简单又强大的数学计算模型。
虽然用的数学不一样,但图灵机的计算能力和 Lambda 算子一样,同时因为图灵机更简单,所以在新兴的计算机领域更受欢迎。
什么是图灵机
图灵机是图灵受打字机的启发而假想出来的一台理论计算设备。假设我们有
- 无限长的纸带,纸带可以存储符号
- 一个状态变量,保存当前状态
- 一个读写头,可以读取和写入 纸带上的符号。
- 一组规则,描述机器做什么。规则是根据当前状态 + 读写头看到的符号,决定机器做什么,结果可能是在纸带写入一个符号,或改变状态,或把读写头移动一格,或执行这些动作的组合。

为了更好理解,我们举一个例子:让图灵机读一个以零结尾的字符串,并计算 1 的出现次数是不是偶数。如果是,在纸带上写一个 1;如果不是,在纸带上写一个 0。
首先要定义“图灵机”的规则:
- 机器的初始状态:由于还没开始计算,当前的 1 的出现次数是 0,是偶数
- 如果当前状态是"偶数", 当前符号是 1,那么把状态更新为"奇数",把读写头向右移动
- 如果当前状态是"奇数", 当前符号是 1,那么把状态更新为"偶数",把读写头向右移动
- 如果当前状态为偶数,当前符号是 0,意味着到了字符串结尾,那么在纸带上写一个 1,并且把状态改成 停机(halt),状态改为"停机" 是因为图灵机已完成计算
- 如果当前状态为奇数,当前符号是 0,意味着到了字符串结尾,那么在纸带上写一个 0,并且把状态改成 停机(halt),状态改为"停机" 是因为图灵机已完成计算
定义好了起始状态 + 规则,就像写好了程序,可以开始输入了。假设把"1 1 0"放在纸带上,有两个 1,是偶数。注意,规则只让读写头向右移动,其他部分无关紧要,为了简单所以留空。

"图灵机"准备好了,开始!机器起始状态为"偶数",看到的第一个数是 1,符合最上面那条规则,所以执行对应的步骤,把状态更新到"奇数", 读写头向右移动一格:

然后又看到 1, 但机器状态是"奇数",所以执行第三条规则,使机器状态变回"偶数",读写头向右移动一格:

最后看到 0,并且机器状态是 偶数,所以执行第二条规则,在纸带上写 1,表示"真" 的确有偶数个 1,然后机器停机。
这就是图灵机的原理,很简单对吧?你可能觉得“有什么大不了的”?
图灵证明了:这个简单假想机器,如果有足够时间和内存,可以执行任何计算。它是一台通用计算机,刚才的程序就是个简单例子,只要有足够的规则,状态和纸带可以创造任何东西,浏览器,魔兽世界,任何东西!当然这样做效率很低,但理论上可行,所以图灵机是很强大的计算模型。
事实上,就可计算和不可计算而言,没有计算机比图灵机更强大,和图灵机一样强大的,叫 "图灵完备"。每个现代计算系统 比如笔记本电脑,智能手机,甚至微波炉和恒温器内部的小电脑,都是"图灵完备"的。
为了回答可判定性问题,他把图灵机用于一个有趣计算问题:"停机问题“。
停机问题
在试想一下,在有些情况下,一台图灵机如果长时间没有输出结果,那么它很可能陷入了死循环或永无止境的计算中。这是我们不愿看到的,因为机器可能运行 1 分钟后停机,也可能运行 10 天半个月甚至几十年才停机,亦或者永远也不会停机,这个很难靠人为判断。
说人话:如果一个数学问题是没有解的,但花了 10 天半个月甚至几十年才发现是没有解决办法,或者永远都没有解决办法,那么就白白花费了很多时间。
假设我们构建出一台图灵机 H,它接收其他图灵机及其输入信息作为输入,并能够判定其是否会停机,就解决了上面的烦恼——构建这样的机器难度虽大,但理论上是可行的。
这就是著名的停机问题(halting problem)。
令 H 表现如下图所示,如果其判定对象会停机则输出 1,反之输出 0。
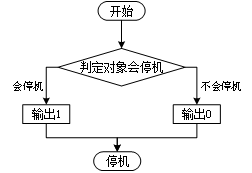
图灵机H运行流程
我们再构建一台图灵机 G,其运行流程如下图所示。如果 H 输出 1,说明 G 会停机,但事实上它将陷入循环;如果 H 输出 0,说明 G 不会停机,但事实上它将停机。
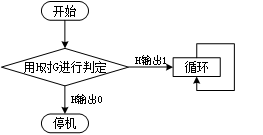
图灵机G运行流程
因此,不存在一台图灵机,可以判定任意图灵机是否会停机。
听起来可能有点绕,其实可以理解为,G 就是故意针对图灵机 H 的。你认为我是不永久的,我就一直永久;如果你认为我是永久的,我就退出;也就是说,你是无法判断我是否会停机的。这说明了不存在这样的图灵机,能够判断停机问题。
更多可以参考如下博客:
如何通俗地解释停机问题(Halting Problem)?https://www.zhihu.com/question/20081359/answer/22043224
停机问题、Chaitin 常数与万能证明方法:http://www.matrix67.com/blog/archives/901
深远影响
图灵的工作参透了数学和计算机的本质关系——计算机是为解决数学问题而诞生的,却又基于数学,因而数学自身的极限也便框定了计算机的能力范围。
图灵虽然证明了没有任何机器可以解决所有数学问题,却也证明了机器可以完成所有人类能完成的计算工作,从如今的应用看来,后一个结论的意义重大得多。
如今的所有通用计算机都是图灵机的一种实现,两者的能力是等价的。当一个计算系统可以模拟任意图灵机(或者说通用图灵机)时,我们称其是图灵完备的(Turing complete);当一个图灵完备的系统可以被图灵机模拟时,我们称其是图灵等效的(Turing equivalent)。
图灵完备和图灵等效成为衡量计算机和编程语言能力的基础指标,如今几乎所有的编程语言也都是图灵完备的,这意味着它们可以相互取代,一款语言能写出的程序用另一款也照样可以实现。
 讲讲图灵对计算机的贡献
讲讲图灵对计算机的贡献





![CSP历年复赛题-P5017 [NOIP2018 普及组] 摆渡车](https://img2024.cnblogs.com/blog/3330618/202406/3330618-20240610134332791-135241159.png)