NOIP2024模拟12:孤帆远影
听了机房同学的讨论,于是T1死磕冒泡和逆序对做法。最后只得了40pts。
思想对了,但不是自己的做法。
还是要坚持自己想,坚持自己可以想出来,不要被任何人带偏。
T1
-
一句话题意:将一个已知序列通过不断“交换相邻位置”的操作调整成不严格单峰状态,问最小的操作次数。
-
有一种猜想是只要钦定了峰顶的位置,那么左右两边是不会交叉的。
- 但这个猜想是错误的,它的证伪可以通过正解来理解
-
正解:假设题目要求我们调成升序,那么答案就是逆序对的数量。
-
现在是什么呢?要求前半段升序后半段降序。
-
那就分开逆序对!
-
具体来说,对于第 \(i\) 个数,想要待在左区间, 就必须穿过左边比它大的每个数,即在它左边的逆序对数量,待在右区间同理.
-
由于峰顶的位置不做限制,所以我们只需要看每个数放左边移动步数少一点,还是放右边少一点,就行了.
-
用树状数组求逆序对即可,只不过是正着倒着各扫一遍.
-
所以此题我很早就陷入了一个误区:枚举峰顶的位置,想来这其实不是题目所求.把自己限制住了!
- 下次考试应该先在草稿本上写出这个想法.尝试一段时间返回去检查自己的思想是不是除了问题的时候,就方便大胆地走出误区.
时间复杂度 \(O(N log N)\)
#include<bits/stdc++.h> #define F(i,l,r) for(int i(l);i<=r;++i) #define G(i,r,l) for(int i(r);i>=l;--i) #define int long long #define lowbit(x) (-x&x) using namespace std; using ll = long long; const int N=2e5+5; int n,pos=0,mx=0; ll L[N],R[N],ans=0; ll a[N],tr[N]; void add(int x){for(;x<=mx;x+=lowbit(x)) tr[x]++; } int ask(int x){int res=0;for(;x>=1;x-=lowbit(x)) res+=tr[x];return res; } signed main(){//freopen("inde.in","r",stdin);//freopen("inde.out","w",stdout);ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin>>n;F(i,1,n) cin>>a[i],mx=max(mx,a[i]); F(i,1,n){add(a[i]);L[i]=i-ask(a[i]);}memset(tr,0,sizeof(tr));G(i,n,1){add(a[i]);R[i]=n-i+1-ask(a[i]);}F(i,1,n){//the fjxans+=min(L[i],R[i]); }cout<<ans;return 0; }
T2
-
一句话题意:给定一个起点,你现在需要依次抵达 \(n\) 个目标区间,既可以亲自去,也可以请别人代劳,但花费都是起终点之间的距离(允许亲自走一半再代劳一半).问最少的花费.
-
有点儿抽象,还没有完全理解,尝试着解释一下:
-
记 \(f[i][j]\) 表示第 \(i\) 次游历最终到达 \(j\) 的最小花费.
- 首先从 \(f[i-1]\) 继承dp值
- 对于操作1: \(j\) 离 \([l_i,r_i]\) 的最近距离即为此部分贡献.
- 对于操作2:用 \(f[i][j]+1\) 更新 \(f[i][j-1]\) 和 \(f[i][j+1]\)
-
最关键的一步:根据操作2,对于每个 \(i\), 将 \(f[i][j]\) 看成关于 \(j\) 的函数,则一定长这个样子:
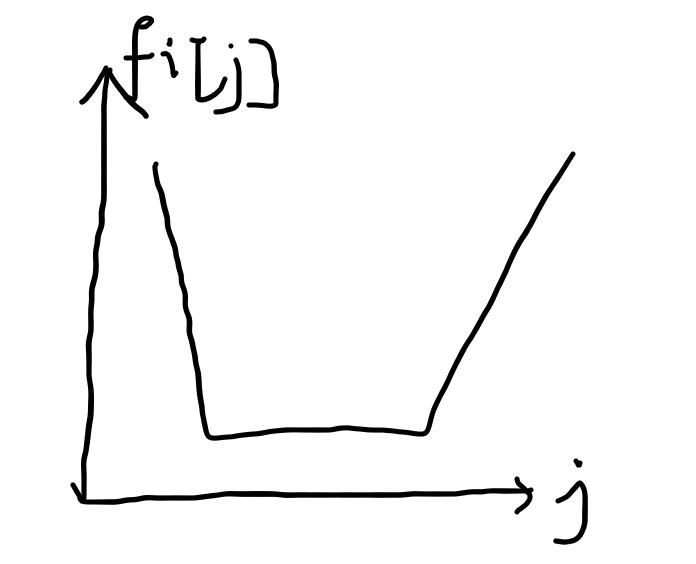
-
转移时,维护中间平的那一段,最后得到的贡献一定就是最优的.(感性理解一下)
-
时间复杂度 \(O(N)\)
#include<bits/stdc++.h> #define F(i,l,r) for(int i(l);i<=r;++i) #define G(i,r,l) for(int i(r);i>=l;--i) #define int long long using namespace std; using ll = long long; const int N=5e5+105; int n,x; signed main(){ // freopen("festival.in","r",stdin); // freopen("festival.out","w",stdout);ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin>>n>>x; int l=x,r=x,L,R;ll ans=0;while(n--){cin>>L>>R;if(l<=R && L<=r){if(L>l) l=L;if(R<r) r=R;}if(R<l) ans+=l-R,r=l,l=R;if(L>r) ans+=L-r,l=r,r=L;}cout<<ans;return 0; }
T3
-
\(O(NlogN)\) 求\(LIS\) 的板题,只不过带了个系数而已.
-
理解:\(C_i\)的系数只影响后续 \(C_{i+1}\) 的判断,而不影响当前判断.
-
唯一的细节就是带系数之后的数不一定比原来小,要取 min.
#include<bits/stdc++.h> #define F(i,l,r) for(int i(l);i<=r;++i) #define G(i,r,l) for(int i(r);i>=l;--i) #define lowbit(x) (-x&x) #define int long long using namespace std; using ll = long long; const int N=1e6+5; int f[N],a[N],b[N]; int n; signed main(){//freopen("geranium.in","r",stdin);//freopen("geranium.out","w",stdout);ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin>>n;F(i,1,n) cin>>a[i];F(i,1,n) cin>>b[i]; int ans=0;F(i,1,n) f[i]=2e18;F(i,1,n){int pos=lower_bound(f+1,f+ans+1,a[i])-f;f[pos]=min(f[pos],a[i]*b[pos]); ans=max(ans,pos);}cout<<ans<<"\n";return 0; }





![CSP历年复赛题-P5017 [NOIP2018 普及组] 摆渡车](https://img2024.cnblogs.com/blog/3330618/202406/3330618-20240610134332791-135241159.png)