IEEE754浮点数表示形式
IEEE754浮点数官方文档:https://ieeexplore.ieee.org/document/8766229

-
浮点数的上述表示形式,既没有规定阶码和尾数的位数,也没有规定阶码和尾数采用的机器码形式(原码、反码、补码和移码)。实际上,直到20世纪80年代初,浮点数表示形式还没有统一标准,不同厂商计算机内部浮点数表示形式可能不同。
-
不同体系结构的计算机之间进行数据传送或程序移植时,必须进行数据格式的转换,并且数据格式转换还会带来运算结果的不一致。因此,美国电气及电子工程师协会(Institute of Electrical and Electronics Engineers,IEEE)于1985年发布 了浮点数标准IEEE754。
-
目前,几乎所有计算机都采用IEEE 754标准表示浮点数。
IEEE754标准主要包括两种基本的浮点数格式:
- 32位单精度浮点数,对应C语言中的float型。
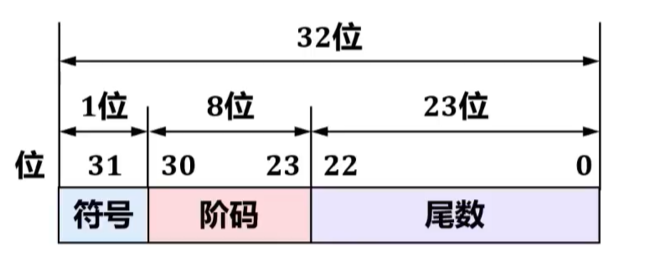
其中:
- 符号:取值0表示正数;取值1表示负数。
- 阶码:定点整数,用移码表示。
- 尾数:定点小数,用原码表示。
- 64位双精度浮点数,对应C语言中的double型。

回顾一下移码定义:
假设真值x为定点整数,n为x的移码表示中数值位的位数(比特数量)。[x]移=x+\(2^{n}\), -\(2^{n}\)≤x<\(2^{n}\)
移码的优点:
- 最小真值的移码为全0,最大真值的移码为全1,符合人们的习惯。
- 真值0在移码中只有一种表示。
- 移码保持了真值原有的大小顺序,可以直接比较大小。
- 当浮点数的阶码用移码来表示时,就能很方便地比较阶码的大小。
- 不考虑移码的符号位看作无符号二进制数
[x]移=x+\(2^{n}\), -\(2^{n}\)≤x<\(2^{n}\)
[x]移=x+\(2^{7}\), -\(2^{7}\)≤x<\(2^{7}\)
在IEEE754浮点数标准中,32位单精度浮点数的8位阶码尽管采用移码表示,但采用偏移常数是\(2^{7}\)-1=127,而不是标准移码的\(2^{7}\)=128。
[x]移=x+(\(2^{7}\)-1), -\(2^{7}\)≤x<\(2^{7}\)
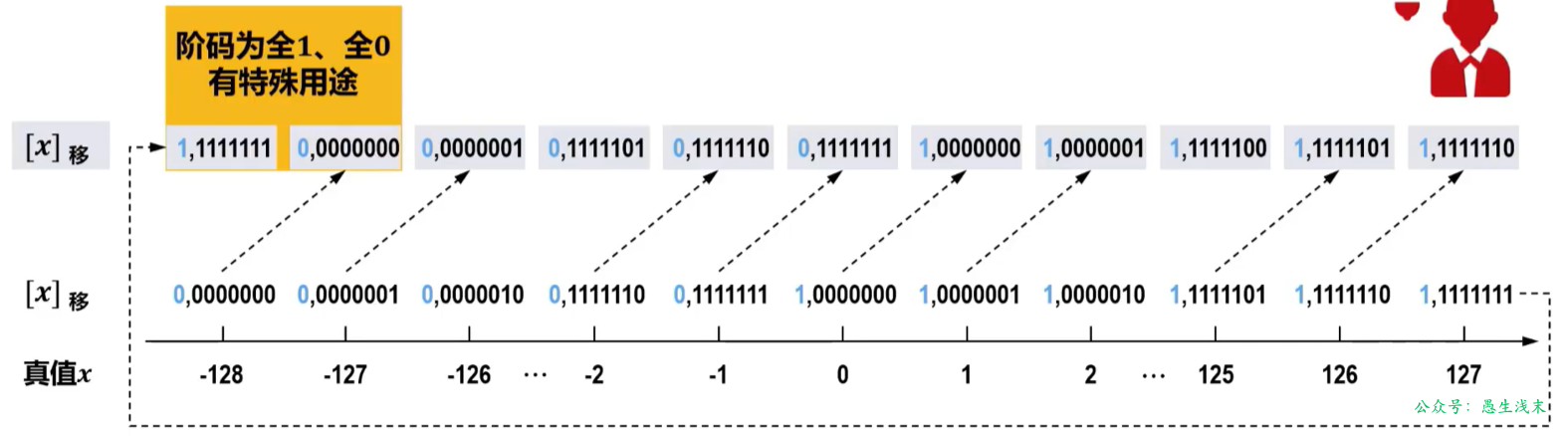
为什么偏移常数不采用标准的128,而采用127?
采用偏移常数128表示的最小规格化数的倒数会发生溢出,而采用偏移常数127表示的任何一个规格化数的倒数则不会溢出。
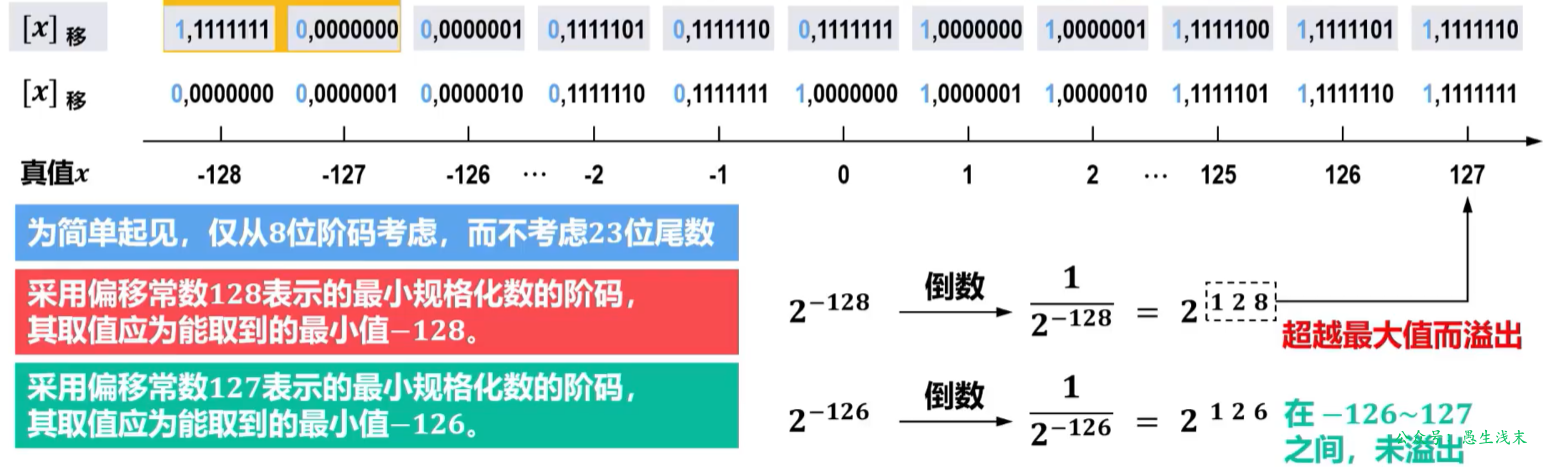
下面以32位单精度浮点数为例介绍IEEE754单精度浮点数标准:
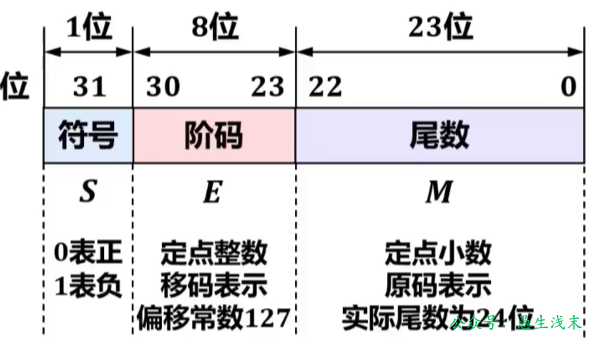
- 符号:取值0表示正数;取值1表示负数。
- 阶码:定点整数,用移码表示,偏置常数27—1=127。
- 尾数:定点小数,用原码表示。符号位前移到最左侧。相邻左侧隐藏一个1,表示数值而不表示符号。尾数实际有24位,但不保存隐藏的那个1,只保存23位,节省的比特位可用于提高尾数的精度。完整的尾数形式为1.M
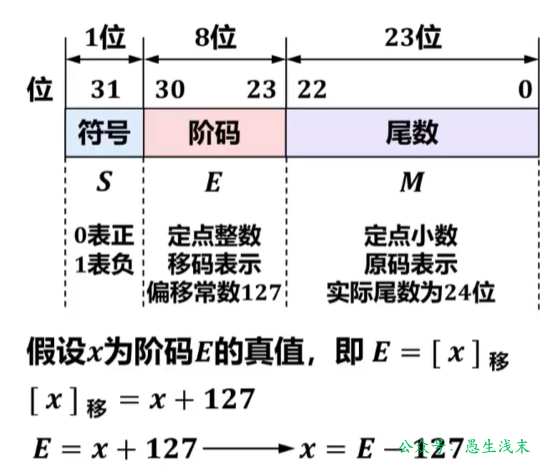
32位浮点数标准示意如下:
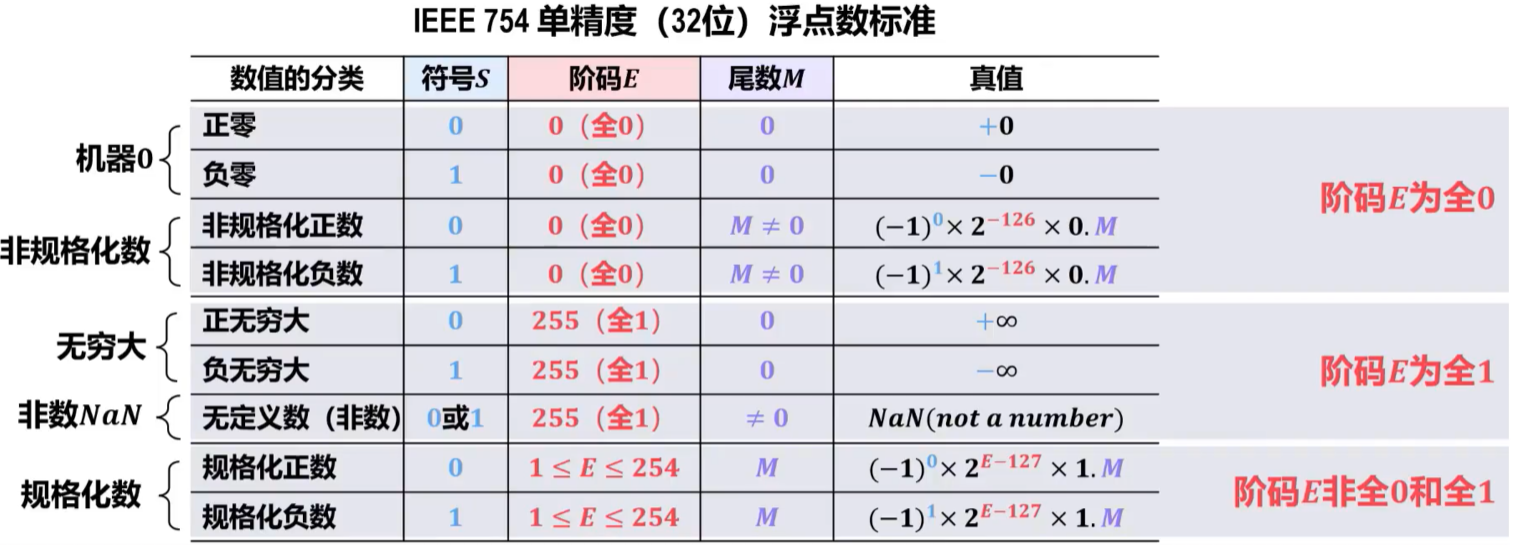
- 非数NaN用于表示\(\frac {0}{0}\)、\(\frac {∞}{∞}\)、0×∞、负数的平方根等。部分非数NaN运算结果可能会产生异常。
- 非规格化数可用于处理阶码下溢,使得出现比最小规格化数还小的数时程序也能继续进行下去。
- 引入无穷大数可使计算过程出现异常的情况下程序能继续执行,并且可为程序提供错误检测功能。例如非0浮点数除0运算的结果就是无究大,因此非0浮点数除不会像整型数除0一样产生严重错误。
32位浮点数和64位浮点数对比:


【例题1】将十进制数408.6875转换成IEEE754单精度浮点数的十六进制机器码。
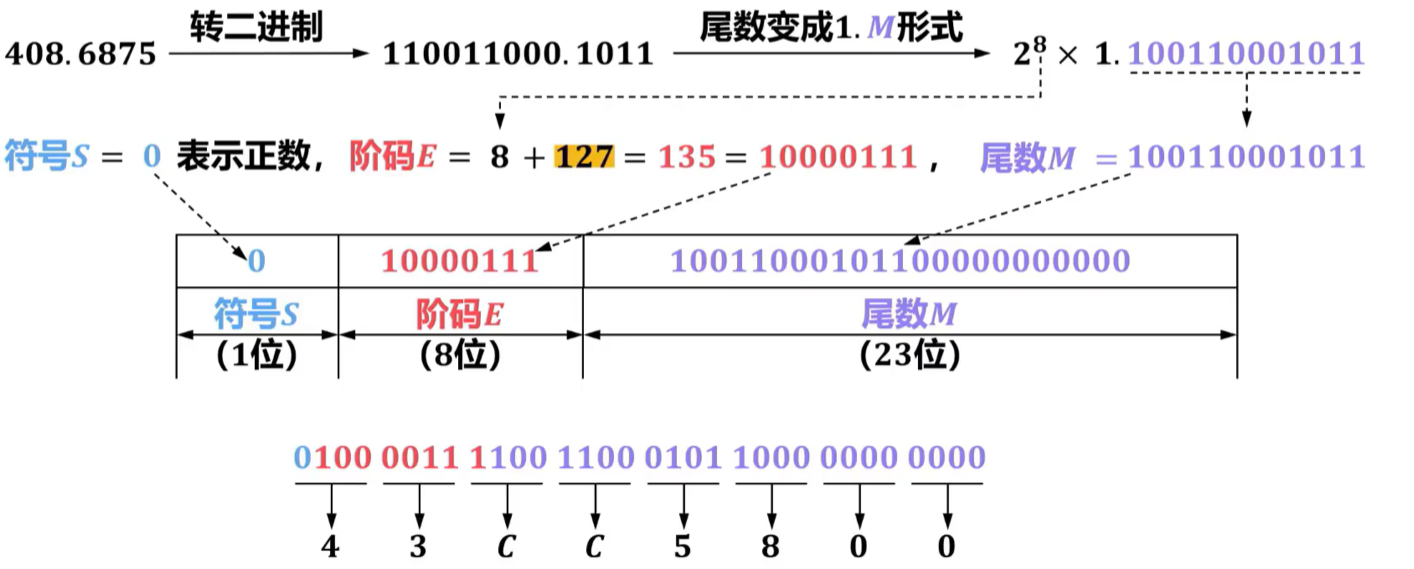
【例题2】若C1830000是某个IEEE754单精度浮点数的十六进制机器码,求其对应的十进制值。

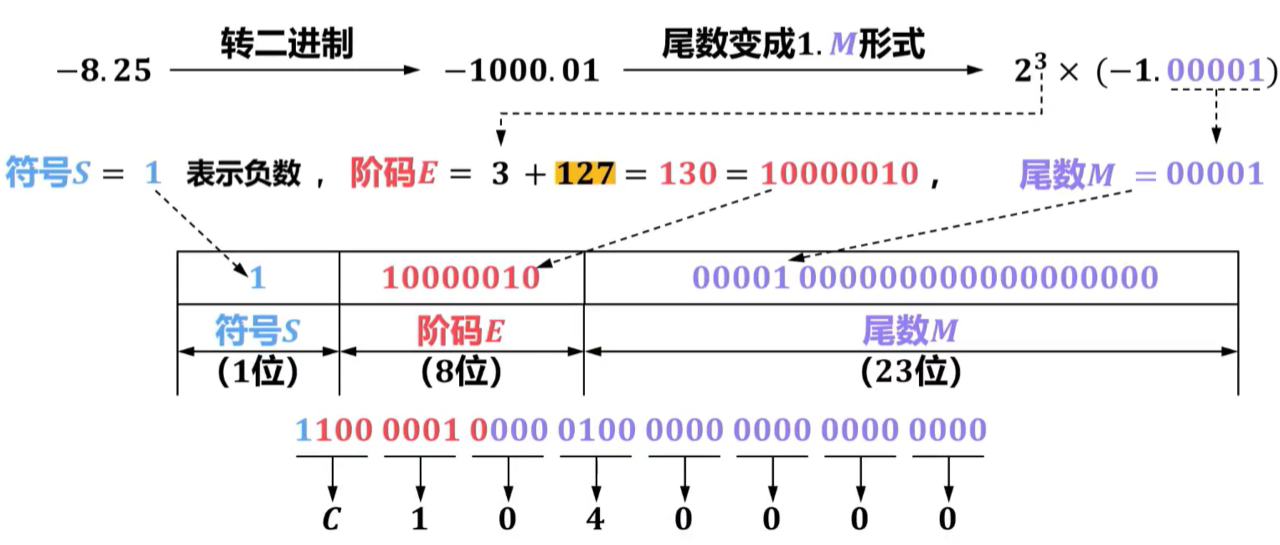
【2011年题13】float型数据通常用IEEE 754单精度格式表示。若编译器将float型变量x分配一个32位浮点寄存器FR1中,且x=—8.25,则FR1的内容是(A)。
A. C104 0000H
B. C242 0000H
C. C184 0000H
D. C1C2 0000H
【2013年题13】某数采用IEEE754单精度浮点数格式表示为C640000H,则该数的值是(A)。
A. -1. 5× \(2^{13}\)
B.-1.5× \(2^{12}\)
C.-0. 5 × \(2^{13}\)
D.-0.5×\(2^{12}\)

【2014年题14】float型数据常用IEEE 754单精度浮点格式表示。假设两个float型变量x和y分别存放在32位寄存器f1和f2中,若(f1)=CC900000H,(f2)=B0C00000H, 则x和y之间的关系是(A)。
A.x<y且符号相同
B.x<y且符号不同
C.x>y且符号相同
D.x>y且符号不同


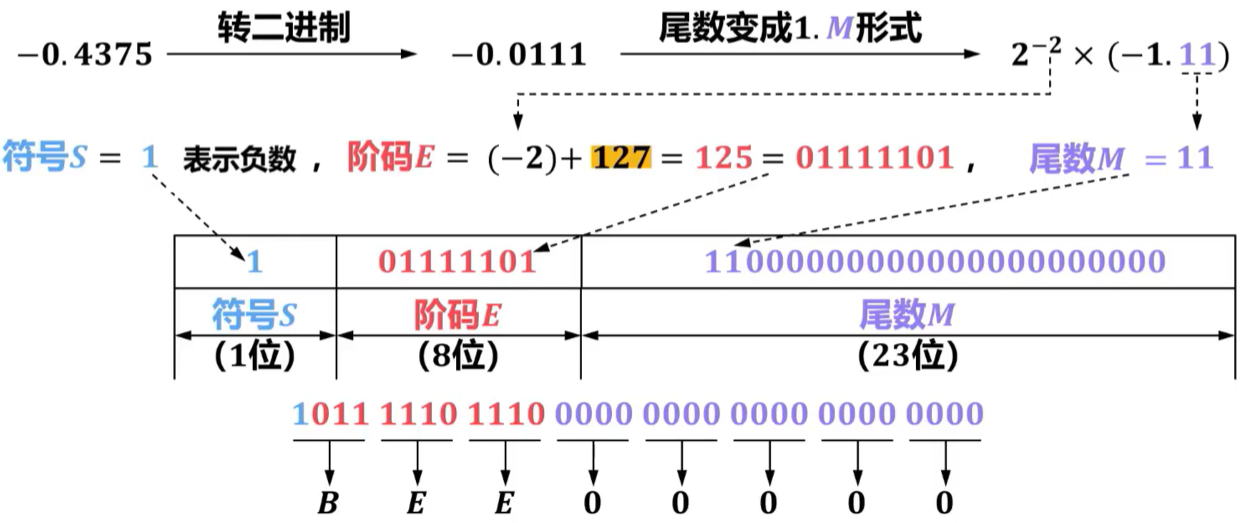
【2022年 题14】—0.4375的IEEE754单精度浮点数表示为(A)
A. BEEO 0000H
B. BF60 0000H
C. BF70 0000H
D. COEO 0000H
IEEE754单精度(32位)浮点数表示范围:



【2012年题14】float类型(即IEEE754单精度浮点数格式)能表示的最大正整数是(D)。
A. 2126- 2103
B.2127-2104
C. 2127- 2103
D.2128-2104
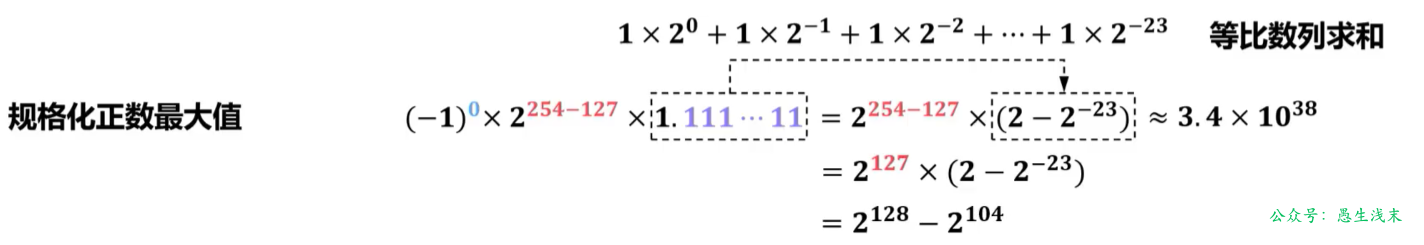
【2018年题14】IEEE754单精度浮点格式表示的数中,最小的规格化正数是(A)。
A. 1.0 X \(2^{-126}\)
B. 1. 0 X \(2^{-127}\)
C. 1. 0 X \(2^{-128}\)
D.1.0×2\(2^{-149}\)
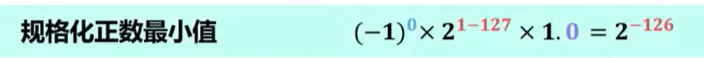
【2021年题14】下列数值中,不能用IEEE754浮点格式精确表示的是(A)。
A. 1. 2
B. 1. 25
C. 2.0
D. 2. 5

对于无限循环小数,通常只能采用舍入的方式近似表示,因此会带来数据表示的误差。这种误差会在计算的过程中不断累积放大,可能导致严重后果。

综上所述,程序员使用二进制浮点数编程时一定要非常小心,要充分考虑浮点数运算可能带来的计算误差,尽量避免对浮点数进行直接比较,在一些对误差极其敏感的情况下,建议采用十进制浮点数进行运算。
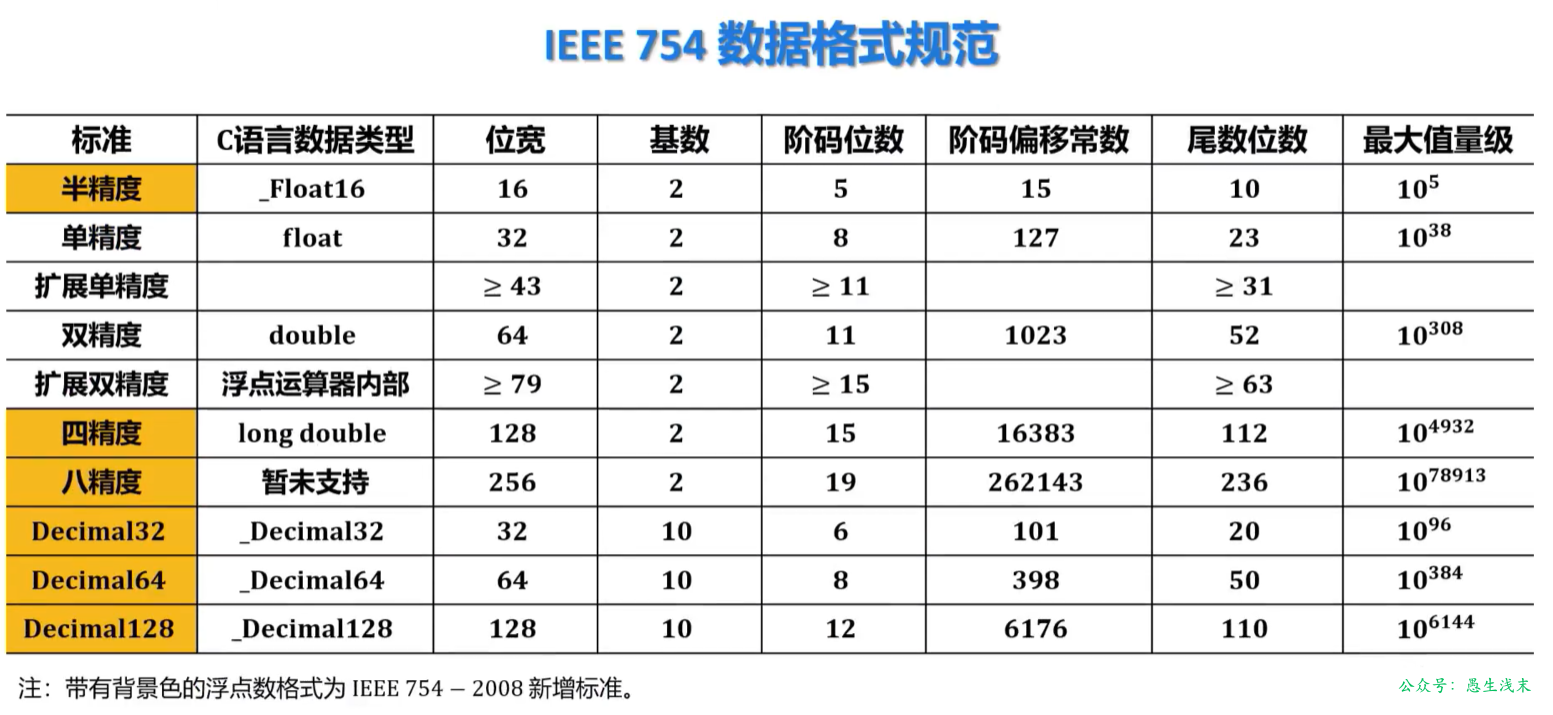
IEEE754其他浮点数标准:
推荐阅读:
- 计算机基础知识之原码、补码、反码和移码
- 计算机基础知识之浮点数的表示
欢迎关注公众号:愚生浅末