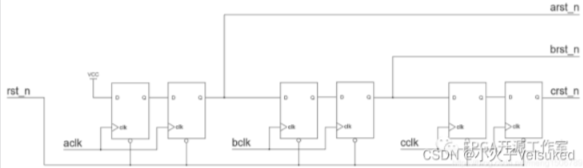
基环树的定义为:一个有向或无向图中,只含有一个环的图,形式化的表达为:
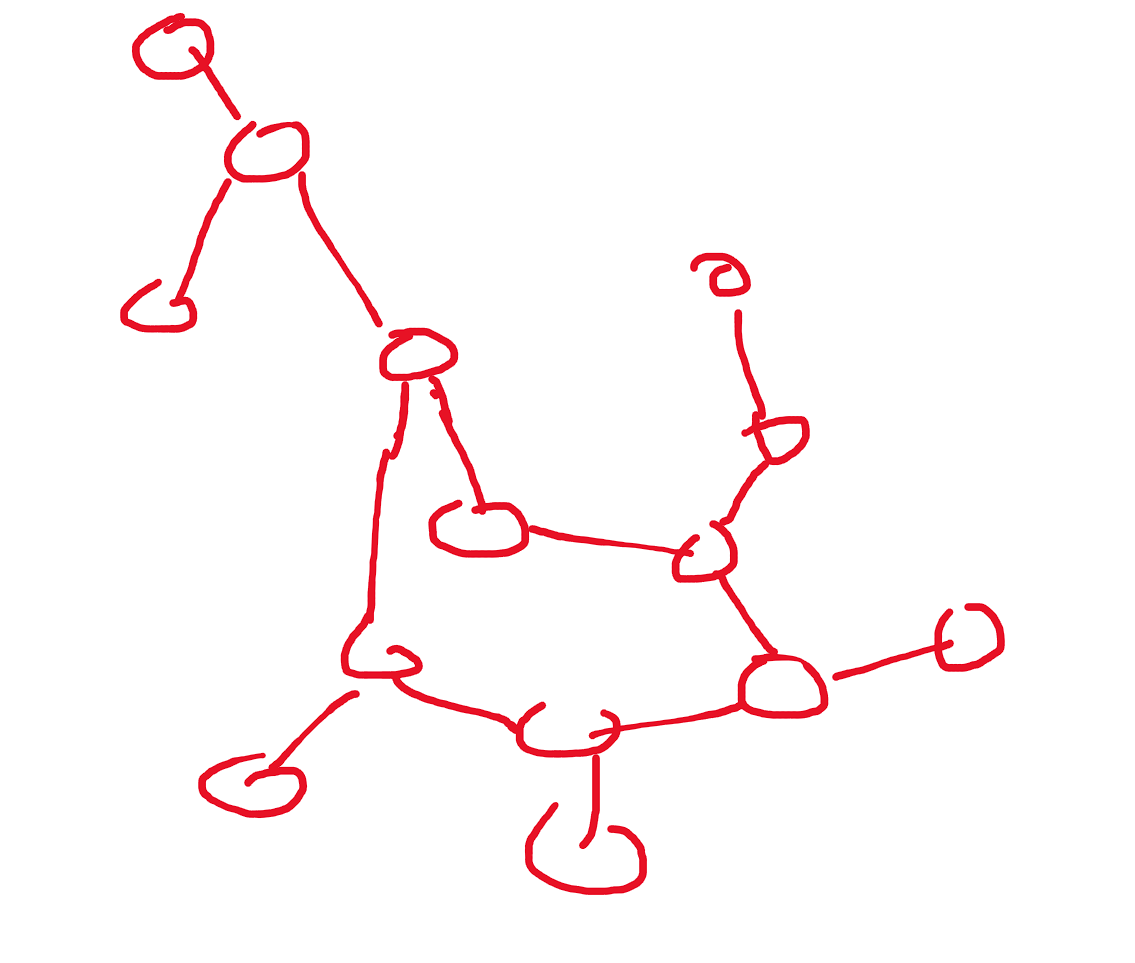
关于这种形状关键点主要在于找环,那么我们可以一步一步的去寻找,当这个点走着走着走到了某个环里,我们可以直接遍历整个环,然后打个标记,这样环就找到了
具体的例题:
E - Reachability in Functional Graph
本题就是一个基环树森林,即不同的连通块,每个块内可能存在一个基环树,那么我们直接暴力的找出来每个环,并且算出环的节点个数,那么每个点的贡献就是,从这个点出发到环内某一节点经过的边数+环的大小,然后再直接进行记忆化搜索即可:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10,mod=1e9+7;
signed main()
{std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);int n; cin>>n;vector<int>a(n+1);for(int i=1;i<=n;i++) cin>>a[i];vector<int>vis(n+1),dp(n+1); // vis 数组是用来标记这个点是否被遍历过// dp 环中每个点的贡献for(int i=1;i<=n;i++){if(vis[i]) continue; //如果被遍历到了,直接跳过int u=i;while(true){ //一直遍历下去if(vis[u]){ if(vis[u]==i){ //如果是第一次被标记,也就是某个环的入口,我们就计算一下这个环int x=a[u],cnt=1;while(x!=u){ //走回来就停止cnt++,x=a[x];}dp[u]=cnt,x=a[u];while(x!=u){dp[x]=cnt,x=a[x]; //每个节点的贡献都是这个环的大小}break;}}vis[u]=i,u=a[u]; //向下传点}}function<int(int)>dfs;dfs=[&](int u)->int{if(dp[u]) return dp[u];return dp[u]=dfs(a[u])+1;};int res=0;for(int i=1;i<=n;i++) res+=dfs(i);cout<<res;return 0;
}