虚树

虚树

什么是虚树

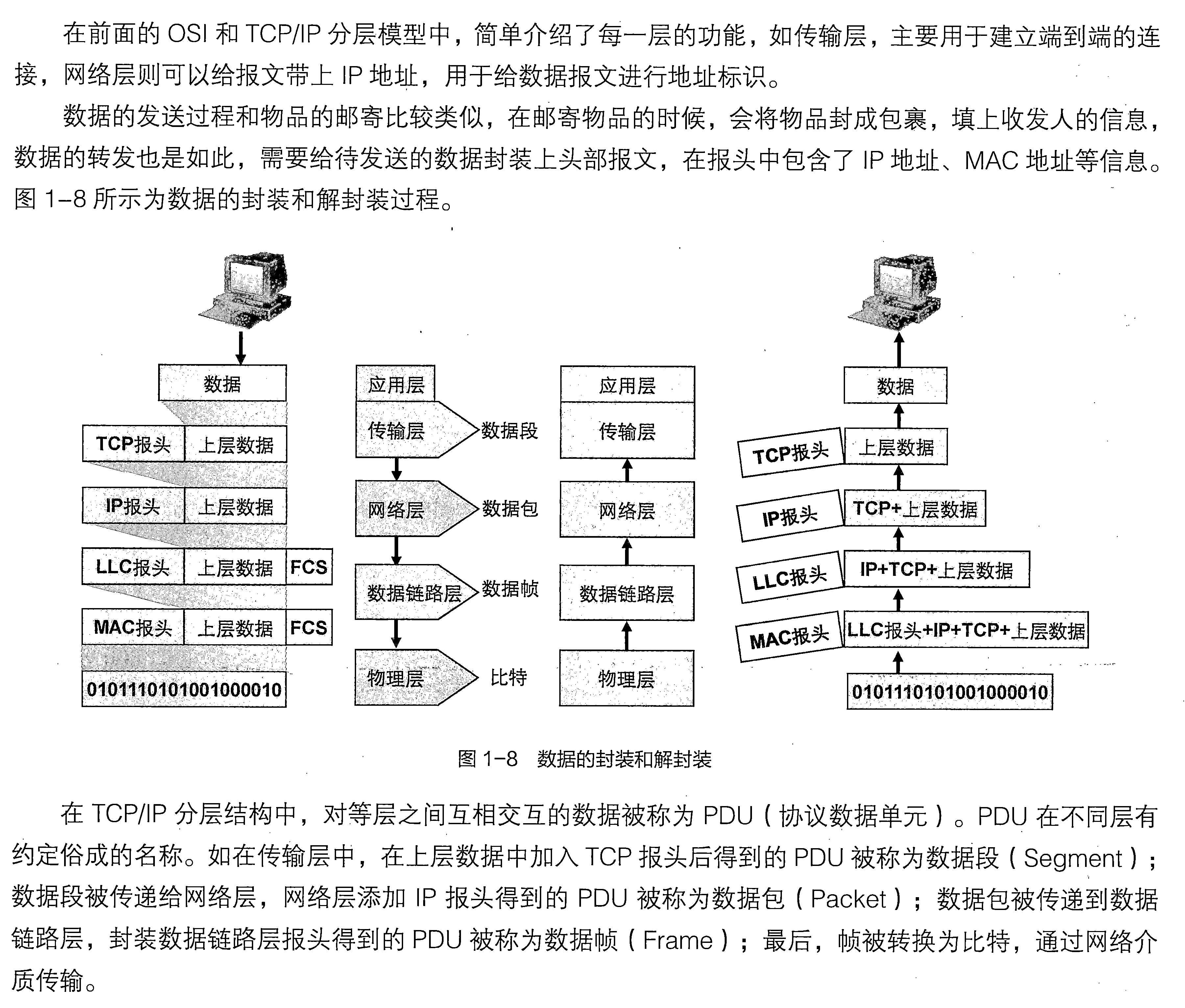
虚树常常被用在树形\(dp\)中。当一次询问仅仅涉及到整棵树中少量节点时为每次询问都对整棵树进行\(dp\)在时间上是不可接受的。此时，我们建立一棵仅仅包含部分关键节点的虚树，将非关键节点构成的链简化成边或是剪去，在虚树上进行\(dp\)。
虚树包含所有的询问点及它们之间的\(lca\)。显然虚树的叶子节点必然是询问点，因此对于某次含有\(k\)个点的询问，虚树最多有\(k\)个叶子节点，从而整棵虚树最多只有\(2^{k-1}\)个节点（这会在虚树变为二叉树形态时达到）。

建立虚树之前

我们需要：

• 预处理出原树的\(dfs\)序以及\(dp\)可能用到的一些其他东西。
• 高效的在线\(LCA\)算法，单词询问\(O(log n)\)的倍增和树剖
• \(O(1)\)的\(RMQ/ST\)
• 将询问点按\(dfs\)序排序

如何建立虚树

最右链是虚树构建的一条分界线，表明其左侧部分的虚树已经完成构建。我们使用栈来维护最右链，\(top\)为栈顶位置。值得注意的是，最右链上的边并没有被加入虚树，这是因为在接下来的过程中随时会有某个\(lca\)插入到最右链中。
初始无条件将第一个询问点加入栈中。
将接下来所有的询问点顺次加入。假设该询问点为\(now\)，\(lc\)为该点和栈顶点的\(LCA\)（即\(lc=LCA(stak[top],now)\)）。由于\(lc\)是\(stak[top]\)的祖先，\(lc\)必然在我们维护的最右链上。
然后考虑\(lc\)和\(stak[top]\)及栈中第二个元素\(stak[top-1]\)的关系。

情况一：

\(lc=stak[top]\)，也就是说，\(now\)在\(stak[top]\)的子树中。

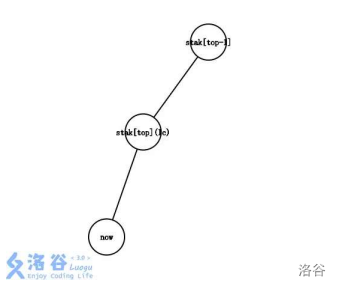
这时候，我们只需要把\(now\)入栈，即把它加到最右链的末端即可。

情况二：

\(lc\)在\(stak[top]\)和\(stak[top-1]\)之间。

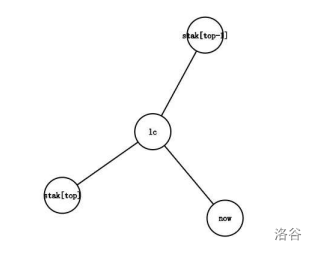
显然，此时最右链的末端从\(stak[top-1]\to stak[top]\)变成了\(stak[top-1]\to lc\to stak[top]\)，我们需要做的，首先是把边\(lc-stak[top]\)加入虚树，然后把\(stak[top]\)出栈，把\(lc\)和\(now\)入栈。

情况三：

\(lc=stak[top-1]\)。

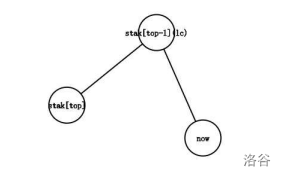
这种情况和第二种差不多，只是lc不用入栈了。

情况四：

此时有\(dep[lc]<dep[stak[top-1]]\)。\(lc\)已经不在\(stak[top-1]\)的子树中了，甚至也未必在\(stak[top-2]，stak[top-3]\)……的子树中了。

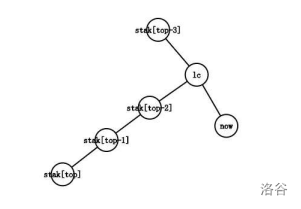
以图中为例，最右链从\(stak[top-3]\to stak[top-2]\to stak[top-1]\to stak[top]\)变成了\(stak[top-3]\to lc\to now\)。我们需要依次将最右链的末端剪下，将被剪下的边加入虚树，直到不再是情况四。
就上图而言，循环会持续两轮，将\(stak[top],stak[top-1]\)依次出栈，并且把边\(stak[top-1]-stak[top],stak[top-2]-stak[top-1]\)加入虚树中，随后通过情况二完成构建。
当最后一个询问点加入之后，再将最右链加入虚树，即可完成构建。

一些问题

1.如果栈中仅仅有一个元素，此时stak[top-1]是否会出问题？
对于栈，我们从1开始储存。那么在这种情况下，\(stak[top-1]=0\)，并且\(dep[0]=0\)。此时\(dep[lc]>dep[stak[top-1]]\)恒成立。也就是说，\(stak[0]\)扮演了深度最小的哨兵，确保了程序只会进入情况一和二。

2.如何在一次询问结束后清空虚树？
不能直接对图进行清空，否则复杂度会退化到\(O(n)\)，这是无法承受的。在\(dfs\)的过程中每当访问完一个节点就进行清空即可。

例题1：[SDOI2011] 消耗战

首先来看朴素的树形dp。
设\(dp_(i)\)表示使i不与其子树中任意一个关键点连通的最小代价。设\(w(a,b)\)表示a与b之间的边的权值。
则枚举i的儿子v：

• 若v不是关键点：\(dp(i)=dp(i)+min\{dp(v),w(i,v)\}\)
• 若v是关键点：\(dp(i)=dp(i)+w(i,v)\)

但我们可以发现树中的很多节点都是没有用的，所以我们需要浓缩信息，把一棵大树浓缩成一棵小树，即建立虚树。
具体地，我们先在栈中添加节点1，然后按照dfs序从小到大添加关键节点。添加的过程按照上述建立即可。
最后在虚树上跑dp即可。
值得注意的是，即使当前节点是关键节点，用不到\(dp(u)\)的值，但仍要对其儿子进行dfs，因为清空虚树需要对整个虚树进行遍历。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 5e5 + 3;
const ll inf = LLONG_MAX;
int dfn[N], dep[N], fa[N][21];
ll minv[N];  //维护从根节点到该点的最小边权，因为要拆代价最小的边
int h[N];
bool vis[N];
int n, m, k, tot;
int stak[N], top;
struct Tree {struct edge {int to, nxt;ll val;} e[N << 1];int head[N], cnt;  //存原图 inline void add(int x, int y, ll v) {e[++cnt].nxt = head[x];head[x] = cnt;e[cnt].to = y;e[cnt].val = v;}inline void dfs(int u, int fath) {dfn[u] = ++tot;fa[u][0] = fath;for (rg int i = 1; i <= 19; i++) {fa[u][i] = fa[fa[u][i - 1]][i - 1];}for (rg int i = head[u]; i; i = e[i].nxt) {rg int v = e[i].to;if (v == fath) continue ;dep[v] = dep[u] + 1;minv[v] = min(minv[u], e[i].val);dfs(v, u);}}
} T;
struct VirtualTree {struct edge {int to, nxt;} e[N << 1];int head[N], cnt;  //存虚树，建单向边 inline void add(int x, int y) {e[++cnt].nxt = head[x];e[cnt].to = y;head[x] = cnt;}inline ll dfs(int u) {rg ll sum = 0, res;for (rg int i = head[u]; i; i = e[i].nxt) {rg int v = e[i].to;sum += dfs(v);}if (vis[u]) res = minv[u];  //是关键节点，必须拆 else res = min(minv[u], sum);  //不是关键节点 vis[u] = false;  //清空虚树head[u] = 0;return res;}inline int LCA(int u, int v) {if (dep[u] < dep[v]) swap(u, v);for (rg int i = 19; i >= 0; i--) {if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];}if (u == v) return u;for (rg int i = 19; i >= 0; i--) {if (fa[u][i] != fa[v][i]) {u = fa[u][i];v = fa[v][i];}}return fa[u][0];}inline void build() {cnt = 0;top = 1;stak[top] = h[1];  //先将1入栈for (rg int i = 2; i <= k; i++) {rg int now = h[i];rg int lc = LCA(now, stak[top]);while (true) {if (dep[lc] >= dep[stak[top - 1]]) {if (lc != stak[top]) {  //不满足为情况一add(lc, stak[top]);if (lc != stak[top - 1]) {  //情况二 stak[top] = lc;} else {  //情况三 top--;}}break;} else {  //情况四add(stak[top - 1], stak[top]);top--;}}stak[++top] = now;  //将now入栈 }while (--top) {add(stak[top], stak[top + 1]);  //将最右链加入虚树 }}
} VT;
inline bool cmp(int a, int b) {return dfn[a] < dfn[b];
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);minv[1] = inf;cin >> n;for (rg int i = 1; i < n; i++) {rg int x, y;rg ll v;cin >> x >> y >> v;T.add(x, y, v);T.add(y, x, v);}T.dfs(1, 0);cin >> m;while (m--) {cin >> k;for (rg int i = 1; i <= k; i++) {cin >> h[i];vis[h[i]] = true;  //给关键点打上标记}sort(h + 1, h + k + 1, cmp);  //按dfs序对关键节点进行排序VT.build();cout << VT.dfs(stak[1]) << "\n";}return qwq;
}

例题2：[SDOI2015] 寻宝游戏

可以发现，对于按照dfs序排序后的关键节点\(\{a_1,a_2,\cdots,a_k\}\)，\(dis(a_1,a_2)+dis(a_2,a_3)+\cdots+dis(a_{k-1},a_k)+dis(a_k,1)\)即为最短路程。
于是预处理出每个节点到根节点的距离来计算任意两节点的距离。对于关键节点，使用set存储即可。
假设插入x，它的dfs序的左右两边分别是y和z。那么答案加上\(dis(x,y)+dis(x,z)-dis(y,z)\)。删除时减去即可。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 1e5 + 3;
int dis[N], dep[N], fa[N][21];
int dfn[N], tot;
int head[N], cnt;
struct edge {int to, nxt;int val;
} e[N << 1];
inline void add(int x, int y, int z) {e[++cnt].to = y;e[cnt].val = z;e[cnt].nxt = head[x];head[x] = cnt;
}
inline void dfs(int u, int fath) {dfn[u] = ++tot;fa[u][0] = fath;for (rg int i = 1; i <= 19; i++) {fa[u][i] = fa[fa[u][i - 1]][i - 1];}for (rg int i = head[u]; i; i = e[i].nxt) {rg int v = e[i].to, w = e[i].val;if (v == fath) continue ;dep[v] = dep[u] + 1;dis[v] = dis[u] + w;dfs(v, u);}
}
inline int LCA(int u, int v) {if (dep[u] < dep[v]) swap(u, v);for (rg int i = 19; i >= 0; i--) {if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];}if (u == v) return u;for (rg int i = 19; i >= 0; i--) {if (fa[u][i] != fa[v][i]) {u = fa[u][i];v = fa[v][i];}}return fa[u][0];
}
inline int get_dis(int x, int y) {return dis[x] + dis[y] - 2 * dis[LCA(x, y)];
}
int n, m;
bool vis[N];
struct node {int val;int dfn;bool operator < (const node& tmp) const { return dfn < tmp.dfn; }
};
set<node> s;
set<node>::iterator it;
int ans;
signed main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n >> m;for (rg int i = 1; i < n; i++) {rg int x, y, z;cin >> x >> y >> z;add(x, y, z);add(y, x, z);}dfs(1, 0);while (m--) {rg int x, y, z;rg node nod;cin >> x;if (!vis[x]) s.insert({x, dfn[x]});  //先插入，保证任何时候s中元素个数不为0 it = s.lower_bound({x, dfn[x]});nod = (it == s.begin() ? *--s.end() : *--it);y = nod.val;it = s.upper_bound({x, dfn[x]});nod = (it == s.end() ? *s.begin() : *it);z = nod.val;rg int d = get_dis(x, y) + get_dis(x, z) - get_dis(y, z);if (!vis[x]) {vis[x] = true;ans += d;} else {s.erase({x, dfn[x]});vis[x] = false;ans -= d;}cout << ans << "\n";}return qwq;
}

例题3：[HEOI2014] 大工程

先建虚树。
首先来看代价和：
可以发现，一条与询问节点相连的边对代价和的贡献为该询问节点的子树中询问节点的个数（包括该节点）乘不在该子树中的询问节点个数再乘边权，即\(siz[u]* (k-siz[u]) * w\)，其中\(siz[u]\)表示u节点的子树内询问节点的个数。
再来看最大代价：
令\(maxx[u]\)表示u的子树中最长链的长度，每次用已经遍历过的子树中的最长链与当前子树中的最长链相拼来更新答案。
对于最小代价：
令\(minn[u]\)表示u的子树中最短链的长度，初始时将询问节点设为0，非询问节点设为极大值，这样，若u为询问节点，则v子树中的最短链只需加上\(dis(u,v)\)就是答案；若u为非询问节点，则v子树中的最短链拼上已经遍历过的子树中的最短链来更新答案。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
using namespace std;
const int N = 1e6 + 3, inf = 2e9;
int n, q, k;
int d[N];
bool vis[N];
int dep[N], fa[N][21];
int dfn[N], tot;
inline bool cmp(int a, int b) {return dfn[a] < dfn[b];
}
inline int LCA(int u, int v) {if (dep[u] < dep[v]) swap(u, v);for (rg int i = 20; i >= 0; i--) {if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];}if (u == v) return u;for (rg int i = 20; i >= 0; i--) {if (fa[u][i] != fa[v][i]) {u = fa[u][i];v = fa[v][i];}}return fa[u][0];
}
struct Tree {int head[N], cnt;struct edge {int to, nxt;} e[N << 1];inline void add(int x, int y) {e[++cnt].to = y;e[cnt].nxt = head[x];head[x] = cnt;}inline void dfs(int u, int fath) {dep[u] = dep[fath] + 1;dfn[u] = ++tot;fa[u][0] = fath;for (rg int i = 1; i <= 20; i++) {fa[u][i] = fa[fa[u][i - 1]][i - 1];}for (rg int i = head[u]; i; i = e[i].nxt) {rg int v = e[i].to;if (v == fath) continue ;dfs(v, u);}}
} T;
ll ans1;
int ans2, ans3;
int stak[N], top;
struct VirtualTree {int head[N], cnt;struct edge {int to, nxt;} e[N << 1];inline void add(int x, int y) {e[++cnt].to = y;e[cnt].nxt = head[x];head[x] = cnt;}int sum[N], minn[N], maxx[N], siz[N];inline void dfs(int u, int fath) {siz[u] = vis[u];maxx[u] = 0;minn[u] = (vis[u] ? 0 : inf);for (rg int i = head[u]; i; i = e[i].nxt) {rg int v = e[i].to;if (v == fath) continue ;dfs(v, u);}for (rg int i = head[u]; i; i = e[i].nxt) {rg int v = e[i].to, w = dep[v] - dep[u];if (v == fath) continue ;ans1 += 1ll * (k - siz[v]) * siz[v] * w;if (siz[v]) {//因为若u为询问节点则minn[u]为0，此时用minn[v]+w（即当前子树的最短链加dis(u,v)）来更新答案//若u为非询问节点则minn[u]为已经遍历过的子树中的最短链，此时将两链相拼更新答案 ans2 = min(ans2, minn[u] + minn[v] + w); ans3 = max(ans3, maxx[u] + maxx[v] + w);}minn[u] = min(minn[u], minn[v] + w);maxx[u] = max(maxx[u], maxx[v] + w);siz[u] += siz[v];}vis[u] = 0;head[u] = 0;}inline void build() {cnt = 0;top = 1;stak[top] = d[1];for (rg int i = 2; i <= k; i++) {rg int now = d[i];rg int lca = LCA(now, stak[top]);while (true) {if (dep[lca] >= dep[stak[top - 1]]) {if (lca != stak[top]) {add(lca, stak[top]);add(stak[top], lca);if (lca != stak[top - 1]) {stak[top] = lca;} else {top--;}}break;} else {add(stak[top - 1], stak[top]);add(stak[top], stak[top - 1]);top--;}}stak[++top] = now;}while (--top) {add(stak[top], stak[top + 1]);add(stak[top + 1], stak[top]);}}
} VT;
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n;for (rg int i = 1; i < n; i++) {rg int u, v;cin >> u >> v;T.add(u, v);T.add(v, u);}T.dfs(1, 0);cin >> q;while (q--) {cin >> k;for (rg int i = 1; i <= k; i++) {cin >> d[i];vis[d[i]] = true;}sort(d + 1, d + k + 1, cmp);VT.build();ans1 = 0;ans2 = inf;ans3 = 0;VT.dfs(stak[1], 0);cout << ans1 << " " << ans2 << " " << ans3 << "\n";}return qwq;
}

例题4：[HNOI2014] 世界树

首先，要计算每一个点离它最近的议事点，可以通过两遍dfs完成，第一遍用儿子更新父亲，第二遍用父亲更新儿子。
建完虚树后，分成两种情况维护虚树上的点：

• 1.一个虚树点u，如果它在原树上的某个儿子v的整棵子树都没有议事点，那么v子树的大小就能贡献到p。
• 2.对于虚树上的一条边，它的两端u和v（即使是lca也可以），对应到原树上的一条链，要找到这条链上的分界点，一半各属于一个议事点。注意链上的子树的贡献也要算上。

#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
const int N = 3e5 + 3, inf = 2e9;
int n, q, m;
int dfn[N], tot, siz[N], dep[N], fa[N][20];
int h[N], oh[N];
bool vis[N];
int ans[N];
int dp[N], g[N];  //距议事点的最短距离，最近的议事点 
int head1[N], cnt1, head2[N], cnt2;
struct edge {int to, nxt;
} e1[N << 1], e2[N << 1];
inline void add1(int x, int y) {e1[++cnt1].to = y;e1[cnt1].nxt = head1[x];head1[x] = cnt1;e1[++cnt1].to = x;e1[cnt1].nxt = head1[y];head1[y] = cnt1;
}
inline void add2(int x, int y) {e2[++cnt2].to = y;e2[cnt2].nxt = head2[x];head2[x] = cnt2;e2[++cnt2].to = x;e2[cnt2].nxt = head2[y];head2[y] = cnt2;
}
inline bool cmp(int a, int b) {return dfn[a] < dfn[b];
}
inline void dfs(int u, int fath) {dfn[u] = ++tot;dep[u] = dep[fath] + 1;siz[u] = 1;fa[u][0] = fath;for (rg int i = 1; i <= 19; i++) {fa[u][i] = fa[fa[u][i - 1]][i - 1];}for (rg int i = head1[u]; i; i = e1[i].nxt) {rg int v = e1[i].to;if (v == fath) continue ;dfs(v, u);siz[u] += siz[v];}
}
inline int LCA(int u, int v) {if (dep[u] < dep[v]) swap(u, v);for (rg int i = 19; i >= 0; i--) {if (dep[fa[u][i]] >= dep[v]) u = fa[u][i];}if (u == v) return u;for (rg int i = 19; i >= 0; i--) {if (fa[u][i] != fa[v][i]) {u = fa[u][i];v = fa[v][i];}}return fa[u][0];
}
int stak[N], top;
inline void build() {cnt2 = 0;top = 1;stak[top] = 1;for (rg int i = 1; i <= m; i++) {if (h[i] == 1) continue ;rg int now = h[i];rg int lca = LCA(now, stak[top]);while (true) {if (dep[lca] >= dep[stak[top - 1]]) {if (lca != stak[top]) {add2(lca, stak[top]);if (lca != stak[top - 1]) {stak[top] = lca;} else {top--;}}break;} else {add2(stak[top - 1], stak[top]);top--;}}stak[++top] = now;}while (--top) {add2(stak[top], stak[top + 1]);}
}
inline void cal(int x, int y) {  //寻找分割点 rg int u = y, v = y;for (rg int i = 19; i >= 0; i--) {if (dep[fa[u][i]] > dep[x]) u = fa[u][i];  //跳到在原树上对应的x的儿子}ans[g[x]] -= siz[u];for (rg int i = 19; i >= 0; i--) {rg int llen = dep[y] - dep[fa[v][i]] + dp[y];rg int rlen = dep[fa[v][i]] - dep[x] + dp[x];if (dep[fa[v][i]] > dep[x] && (llen < rlen || (llen == rlen && g[y] < g[x]))) v = fa[v][i];}ans[g[y]] += siz[v] - siz[y];ans[g[x]] += siz[u] - siz[v];
}
inline void dfs1(int u, int fath) {  //用儿子更新父亲 dp[u] = inf;for (rg int i = head2[u]; i; i = e2[i].nxt) {rg int v = e2[i].to, w = dep[v] - dep[u];if (v == fath) continue ;dfs1(v, u);if (dp[v] + w < dp[u]) {dp[u] = dp[v] + w;g[u] = g[v];} else if (dp[v] + w == dp[u]) {g[u] = min(g[u], g[v]);}}if (vis[u]) {dp[u] = 0;g[u] = u;}
}
inline void dfs2(int u, int fath) {  //用父亲更新儿子 for (rg int i = head2[u]; i; i = e2[i].nxt) {rg int v = e2[i].to, w = dep[v] - dep[u];if (v == fath) continue ;if (dp[u] + w < dp[v]) {dp[v] = dp[u] + w;g[v] = g[u];} else if (dp[u] + w == dp[v]) {g[v] = min(g[v], g[u]);}cal(u, v);dfs2(v, u);}ans[g[u]] += siz[u];  //需要加上自己 vis[u] = 0;head2[u] = 0;
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n;for (rg int i = 1; i < n; i++) {rg int u, v;cin >> u >> v;add1(u, v);}dfs(1, 0);cin >> q;while (q--) {cin >> m;for (rg int i = 1; i <= m; i++) {cin >> h[i];oh[i] = h[i];vis[h[i]] = true;}sort(h + 1, h + m + 1, cmp);build();dfs1(stak[1], 0);dfs2(stak[1], 0);for (rg int i = 1; i <= m; i++) {cout << ans[oh[i]] << " ";vis[oh[i]] = false;ans[oh[i]] = 0;}cout << "\n"; }return qwq;
}