[lnsyoj118/luoguP3369]普通平衡树-编程知识

[lnsyoj118/luoguP3369]普通平衡树

news/2025/1/4 10:54:36/文章来源:https://www.cnblogs.com/XiaoJuRuoUP/p/18244891/lnsyoj118_luoguP3369

题意

维护一个数据结构，要求支持插入，删除，根据排名查数，根据数查排名，查询前驱，查询后继\(6\)个操作

sol

考虑到后四个查询的操作，会发现使用二叉搜索树(BST)完全可以实现
为了完成这四个操作，需要在每个节点记录\(3\)个值：

\(key\) 表示当前节点的数
\(cnt\) 表示当前节点的数的个数（为了防止出现同一数字出现多次）
\(size\) 表示当前子树的数的个数（为了方便查询排名）

根据排名查数

当处于节点\(u\)时，设当前需要查询的排名为\(rank\)，如果此时节点\(u\)为空节点，说明不存在该数，否则分情况讨论：

如果\(u.lson.size \ge rank\)，说明此时要查询的数一定位于\(u\)的左子树，因此答案为左子树中排名为\(rank\)的数
如果\(u.lson.size + u.cnt \ge rank\)，说明此时要查询的数为\(u.key\)，因此答案就为\(u.key\)
前两条均不满足，则说明此时要查询的数一定位于\(u\)的右子树，又由于需要去除掉左子树和\(u\)的所有数，因此答案为右子树中排名为\(rank - u.lson.size - u.cnt\)的数

代码

int get_key(int u, int rank){if (!u) return INF;if (rank <= tr[tr[u].l].size) return get_key(tr[u].l, rank);if (rank <= tr[tr[u].l].size + tr[u].cnt) return tr[u].key;return get_key(tr[u].r, rank - tr[tr[u].l].size - tr[u].cnt);
}

根据数查排名

当处于节点\(u\)时，设当前需要查询的数为\(x\)，如果此时节点\(u\)为空节点，说明不存在该数，否则分情况讨论：

如果\(x < u.key\)，说明此时要查询的数一定位于\(u\)的左子树，因此答案为左子树中数\(x\)的排名
如果\(x = u.key\)，说明此时要查询的数为\(u.key\)，因此答案为\(u.lson.size + 1\)
前两条均不满足，则说明此时要查询的数一定位于\(u\)的右子树，又由于需要加上左子树和\(u\)的所有数，因此答案为右子树中数\(x\)的排名\(+u.lson.size + u.cnt\)

代码

int get_rank(int u, int key){if (!u) return 0;if (key < tr[u].key) return get_rank(tr[u].l, key);if (key == tr[u].key) return tr[tr[u].l].size + 1;return tr[tr[u].l].size + tr[u].cnt + get_rank(tr[u].r, key);
}

需要注意的是，部分时候为了方便，我们会在BST中加入两个哨兵节点\(-\infty\)与\(+\infty\)，此时由于\(-\infty\)的存在，根据排名查数时的\(rank\)需要\(+1\)，而根据数查排名时的查得的答案需要\(-1\)

查询前驱

当处于节点\(u\)时，设当前需要查询的数为\(x\)，如果此时节点\(u\)为空节点，说明不存在该数，否则分情况讨论：

若\(x \le u.key\)，说明此时要查询的数一定不位于\(u\)的右子树，因此答案为左子树中数\(x\)的前驱
若\(x > u.key\)，说明此时要查询的数可能为\(u.key\)，也可能位于\(u\)的右子树，因此答案为右子树中数\(x\)的前驱与\(u.key\)中的最大值

代码

int get_prev(int u, int key){if (!u) return -INF;if (tr[u].key >= key) return get_prev(tr[u].l, key);return max(tr[u].key, get_prev(tr[u].r, key));
}

查询后继

当处于节点\(u\)时，设当前需要查询的数为\(x\)，如果此时节点\(u\)为空节点，说明不存在该数，否则分情况讨论：

若\(x \ge u.key\)，说明此时要查询的数一定不位于\(u\)的左子树，因此答案为右子树中数\(x\)的前驱
若\(x < u.key\)，说明此时要查询的数可能为\(u.key\)，也可能位于\(u\)的左子树，因此答案为左子树中数\(x\)的前驱与\(u.key\)中的最小值

代码

int get_next(int u, int key){if (!u) return INF;if (tr[u].key <= key) return get_next(tr[u].r, key);return min(tr[u].key, get_next(tr[u].l, key));
}

这样一来，这四个查询操作及两个修改操作的复杂度为\(O(h)\)，\(h\)为BST高度。在随机数据下，\(h\)趋向于\(\log n\)，但由于BST容易被卡的优秀性质，只需递增/递减数据就可以将BST卡成一条链，从而使\(h=n\)，因此，我们需要一些手段来使BST的\(h\)无论何时都接近于\(\log n\)，平衡树应运而生

旋转

BST有一条很好的性质：~~容易被卡~~中序遍历是单调递增的，反过来也成立，如果我们可以通过一些操作，使中序遍历不变，那么这棵树仍是本质相同的BST，而这个能够使中序遍历不变的操作即为旋转，旋转是几乎所有平衡树都需要使用的操作（部分除外，如FHQ-Treap）

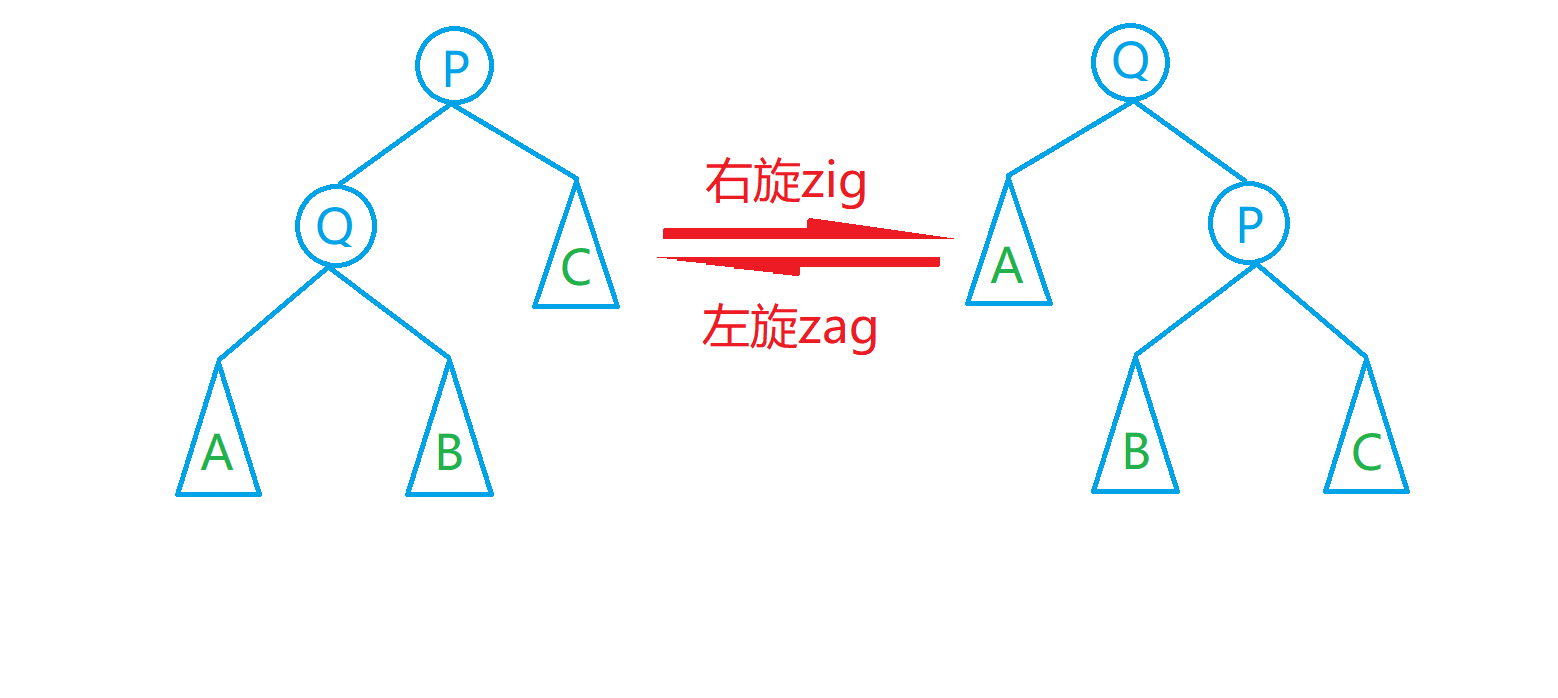
两图中序遍历都为\(A,Q,B,P,C\)
在执行\(zig\)操作时，需要进行三次改变：\(p.lson \to q.rson(B), q.rson \to p, p \to q\)
同理，在执行\(zag\)操作时，也需要进行三次改变：\(q.rson \to p.lson(B), p.lson \to q, q \to p\)
代码

void zig(int &u){int q = tr[u].l;tr[u].l = tr[q].r, tr[q].r = u, u = q;
}void zag(int &u){int q = tr[u].r;tr[u].r = tr[q].l, tr[q].l = u, u = q;
}

需要注意的是，这里的\(u\)指代的是根节点或某个节点的子节点，当执行\(zig\)或\(zag\)时，所对应的节点也要改变，因此需要在函数中传递引用。旋转操作可以视为是BST上三条边所指节点的交换操作

Treap

Treap是OI中较常用的一种平衡树
Treap是Tree和Heap的结合体，它的原理非常简单粗暴：既然BST在随机数据下趋于\(\log n\)，那么我们就把所有数据打乱顺序再插入就好了。显然，在\(99.99\%\)的情况之下，这种方法都是有效的。不过因为大多数平衡树解决的问题都是在线问题，因此我们无法简单地将数据打乱。
Treap给出的解决方案是这样的：对于每一个节点，在插入时赋予它一个随机权值\(val\)，由于可以通过\(zig\)和\(zag\)操作将BST的任一一对父子节点交换而不改变BST的本质，因此我们可以参考二叉堆，插入到对应位置后再向上调整，直到BST中的\(val\)仍然满足二叉堆的性质
对于插入操作，我们先将一个节点插入BST中，然后从下往上判断它是否需要调序；而对于删除操作，我们在BST中找到该节点后，为了方便操作，我们将该节点先调整到叶子结点上，再进行删除。具体代码见下：

void insert(int &u, int key){if (!u) u = create(key); // 没有该节点的话，就创建一个新节点else if (key == tr[u].key) tr[u].cnt ++ ; // 否则直接在节点上添加标记else if (key < tr[u].key){insert(tr[u].l, key);if (tr[tr[u].l].val < tr[u].val) zig(u); // 向上调序}else {insert(tr[u].r, key);if (tr[tr[u].r].val < tr[u].val) zag(u); // 向上调序}
}void erase(int &u, int key){if (!u) return ; // 没有该节点的话，无需处理else if (key == tr[u].key){if (tr[u].cnt > 1) tr[u].cnt -- ; // 如果存在多个标记，直接删除标记else if (tr[u].l || tr[u].r){if (!tr[u].r || tr[tr[u].l].val > tr[tr[u].r].val){zig(u); // 先向下调序erase(tr[u].r, key);}else{zag(u); // 先向下调序erase(tr[u].l, key);}}else u = 0; // 调到叶子节点后直接删除}else if (key < tr[u].key) erase(tr[u].l, key);else erase(tr[u].r, key);
}

需要注意的是，本题的\(size\)是会在旋转、插入、删除操作中随时改变的，类比线段树，我们还需要一个方法来根据子结点的数据反推节点的\(size\)，即PUSHUP
代码：

void pushup(int u){tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + tr[u].cnt;
}

这样的话，我们就通过精巧的操作使BST基本平衡，平均时间复杂度也随之下降为\(O(n \log n)\)，不过值得注意的是，其最坏复杂度仍为\(O(n^2)\)~~，只是如果真的卡出来了，概率堪比十连十金~~

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdlib>using namespace std;const int N = 100005, INF = 0x3f3f3f3f;struct Node{int l, r;int key, val;int cnt, size;
}tr[N];int root, idx;
int n;int create(int key){tr[ ++ idx].key = key;tr[idx].val = rand();tr[idx].cnt = tr[idx].size = 1;return idx;
}void pushup(int u){tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + tr[u].cnt;
}void zig(int &u){int q = tr[u].l;tr[u].l = tr[q].r, tr[q].r = u, u = q;pushup(tr[u].r);
}void zag(int &u){int q = tr[u].r;tr[u].r = tr[q].l, tr[q].l = u, u = q;pushup(tr[u].l);
}void build(){create(-INF), create(INF);root = 1, tr[1].r = 2;pushup(root);
}void insert(int &u, int key){if (!u) u = create(key);else if (key == tr[u].key) tr[u].cnt ++ ;else if (key < tr[u].key){insert(tr[u].l, key);if (tr[tr[u].l].val < tr[u].val) zig(u);}else {insert(tr[u].r, key);if (tr[tr[u].r].val < tr[u].val) zag(u);}pushup(u);
}void erase(int &u, int key){if (!u) return ;else if (key == tr[u].key){if (tr[u].cnt > 1) tr[u].cnt -- ;else if (tr[u].l || tr[u].r){if (!tr[u].r || tr[tr[u].l].val > tr[tr[u].r].val){zig(u);erase(tr[u].r, key);}else{zag(u);erase(tr[u].l, key);}}else u = 0;}else if (key < tr[u].key) erase(tr[u].l, key);else erase(tr[u].r, key);pushup(u);
}int get_rank(int u, int key){if (!u) return 0;if (key < tr[u].key) return get_rank(tr[u].l, key);if (key == tr[u].key) return tr[tr[u].l].size + 1;return tr[tr[u].l].size + tr[u].cnt + get_rank(tr[u].r, key);
}int get_key(int u, int rank){if (!u) return INF;if (rank <= tr[tr[u].l].size) return get_key(tr[u].l, rank);if (rank <= tr[tr[u].l].size + tr[u].cnt) return tr[u].key;return get_key(tr[u].r, rank - tr[tr[u].l].size - tr[u].cnt);
}int get_prev(int u, int key){if (!u) return -INF;if (tr[u].key >= key) return get_prev(tr[u].l, key);return max(tr[u].key, get_prev(tr[u].r, key));
}int get_next(int u, int key){if (!u) return INF;if (tr[u].key <= key) return get_next(tr[u].r, key);return min(tr[u].key, get_next(tr[u].l, key));
}int main(){scanf("%d", &n);build();while (n -- ){int op, x;scanf("%d%d", &op, &x);switch(op){case 1: insert(root, x); break;case 2: erase(root, x); break;case 3: printf("%d\n", get_rank(root, x) - 1); break;case 4: printf("%d\n", get_key(root, x + 1)); break;case 5: printf("%d\n", get_prev(root, x)); break;case 6: printf("%d\n", get_next(root, x)); break;default: break;}}return 0;
}