php:安装phpredisadmin-编程知识

php:安装phpredisadmin

news/2025/1/22 23:05:10/文章来源:https://www.cnblogs.com/architectforest/p/18292572

一，项目代码地址:

https://github.com/erikdubbelboer/phpRedisAdmin

二，下载:

从命令行用wget下载

[root@blog phpredisadmin]# wget https://github.com/erikdubbelboer/phpRedisAdmin/archive/refs/tags/v1.20.0.tar.gz

下载完成后解压缩

[root@blog phpredisadmin]# tar -zxvf v1.20.0.tar.gz

三，安装

移动到你的documentroot目录下

[root@blog phpredisadmin]# mv phpRedisAdmin-1.20.0/ /your/documentroot/phpredisadmin

进入移动后以的目录，安装predis

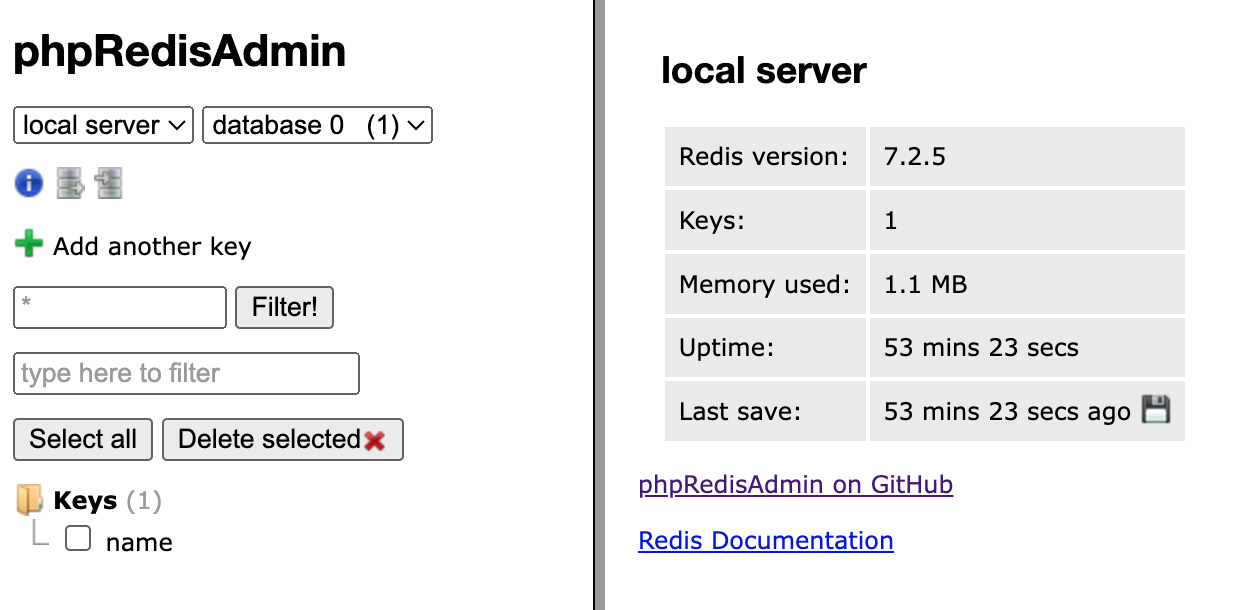
[root@blog phpredisadmin]# git clone https://github.com/nrk/predis.git vendor

四，测试效果:

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/741278.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

数学推导

基本公式（a+b)%mod=(a%mod+b%mod)%mod 设一个任意整数\(A=a*10^n+b*10^{n-1}+...+c\). 由此可以证明 \(A \quad mod \quad m=(((a \quad mod \quad m)*10+b \quad mod \quad m)*10...)+c) \quad mod \quad m\) 该证明可以应用在数位DP点击查看代码 #include<bits/stdc++.h…

OpenDevin 简介：一个有抱负的 AI 驱动的软件开发平台

来源链接：https://medium.com/ai-advances/introduction-to-opendevin-the-aspiring-ai-powered-software-development-platform-11ffc69e60cc 发布时间：2024-05-05T00:40:39.078ZOpenDevin 是一个创新的开源项目，旨在通过引入一个自主的 AI 软件工程师来彻底改变软件开发。…

PM2 ecosystem 服务器自动化部署

一：准备工作 1.1 ：将项目上传至代码管理库（github,gitlab,bitbucket,等） 1.2 ：Windows 和服务器都安装SSH，Git 工具。二：开始 2.1 本地生成ssh key连接服务器//根据邮箱生成ssh key ssh-keygen -t rsa -C "..........@163.com"//仔细看注释 //1.如果生成过…

java推送打卡记录到企微，中文乱码

在开发机中，推送中文能正常显示，部署到windows服务器上，中文显示乱码设置windows环境变量： JAVA_TOOL_OPTIONS: -Dfile.encoding=UTF-8

Linux web服务

Web服务在Linux中存在许多可以提供web服务的软件，httpd、tomcat、nginx等Web通信的基本概念基于B/S架构的网页服务 HTTP HTML【1】、httpd软件 1、httpd软件安装httpd是软件基金会写出的软件基金会（Apache）yum install -y httpdrpm -qa httpd httpd-2.4.37-62.module+el8.9…

jmeter分布式no-gui 测试报告

1、远程测试 https://jmeter.apache.org/usermanual/remote-test.html 2、 3、进行分布式压测是，服务器需要先启动jmeter-sever，启动jmeter-sever建议加上nobup，后开运行，停止服务时，先停master，在停slave，不然可能有问题。linux上具体的压测命令如下：只有一台服务时…

vmware禁止虚拟主机开启后自动时间同步到宿主机

编辑虚拟机 VMX配置文件找到tools.syncTime = "FALSE"并在该行下添加如下七行，注意标点符号 time.synchronize.continue = "FALSE" time.synchronize.restore = "FALSE" time.synchronize.resume.disk = "FALSE" time.synchronize.sh…

转-OAuth2.0 原理流程及其单点登录和权限控制

原文链接单点登录是多域名企业站点流行的登录方式。本文以现实生活场景辅助理解，力争彻底理清 OAuth2.0 实现单点登录的原理流程。同时总结了权限控制的实现方案，及其在微服务架构中的应用。 1 什么是单点登录 1.1 多点登录传统的多点登录系统中，每个站点都实现了本站专用…

【转】-Java反射

Java 反射由浅入深 | 进阶必备原文链接本博文主要记录我学习 Java 反射（reflect）的一点心得，在了解反射之前，你应该先了解 Java 中的 Class 类，如果你不是很了解，可以先简单了解下。一、Java 反射机制参考了许多博文，总结了以下个人观点，若有不妥还望指正：Java 反…

OAuth2.0登录的四种方式

OAuth登录的四种方式 1. 授权码授权码（authorization code）方式，指的是第三方应用先申请一个授权码，然后再用该码获取令牌。这种方式是最常用的流程，安全性也最高，它适用于那些有后端的 Web 应用。授权码通过前端传送，令牌则是储存在后端，而且所有与资源服务器的通信…

C++关于计算浮点数小数位数时遇到的浮点数精确度问题（以及浮点数强制转换问题）

起因是当我想要计算浮点数的小数位位数（利用当浮点数num减去其整数位）我的想法是先分离出小数位，然后每次循环给小数位乘上10，直到不存在小数位时，就会满足当num - (int)num == 0通过这种方式就可以得到小数位的长度 #include <iostream> using namespace std; in…

codeforces 955 div 2 D

题目链接 D. Beauty of the mountains 题目大意解题思路首先记录所有雪山和没有雪山两种山峰的高度差为 \(tot\) ，然后对于每个可能的子矩，我们可以每次给所有山峰都加一或者减一，因此只要计算出矩阵内两种山峰的个数差的绝对值我们就能得到每次操作该子矩阵对tot的贡献 \(…