📙作者简介: 清水加冰,目前大二在读,正在学习C/C++、Python、操作系统、数据库等。
📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。
欢迎点赞 👍 收藏 ⭐留言 📝 如有错误还望各路大佬指正!
✨每一次努力都是一种收获,每一次坚持都是一种成长✨

目录
前言
1. 特殊二叉树
1.1 满二叉树
1.2 完全二叉树
1.3 二叉树的性质
2. 搜索二叉树
3. 练习
📖 题目一
📖 题目二
📖 题目三
总结
前言
在计算机科学领域中,二叉树作为一种重要的数据结构,被广泛应用于各种算法和问题的解决方案中。然而,对于许多人来说,二叉树仍然是一个神秘而复杂的概念。本篇博客将带领你一同深入探索二叉树的内在结构和特性,帮助你建立起对二叉树的全面理解。
1. 特殊二叉树
前边我们已经介绍了树的结构,也了解了普通二叉树,以及二叉树的遍历,今天我们将会继续深入学习二叉树。
1.1 满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。如下图:
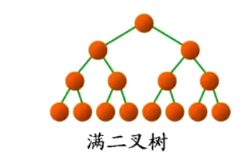
1.2 完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。(直白点说就是:假设有n层,前n-1层为满二叉树,最后一层的节点从左到右依次连接,不会出现一个节点连不满的情况)
如下图:
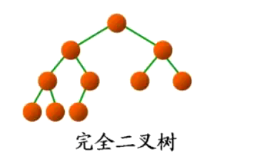
这样的它就不属于完全二叉树:
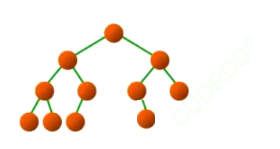
因为从左到右,有节点没有满(从左到右节点必须连满,不能出现有空)。
1.3 二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2⁽ⁱ⁻¹⁾个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2ʰ-1
- 对任何一棵二叉树, 如果度为0其叶结点个数为 , 度为2的分支结点个数为 ,则有 n₀=n₂+1(下标为二叉树的度)
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log₂(n+1)
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
2. 搜索二叉树
上述的二叉树对于数据存储没什么特别规定与要求,属于普通二叉树大类,对于普通二叉树来说,没有增删查改,普通二叉树的增删查改在现实应用中是没有意义的(数据没有特殊规定,无法确认新增节点的位置)。所以这里我们再来介绍一下其他的二叉树——搜索二叉树
什么是搜索二叉树?如下图:
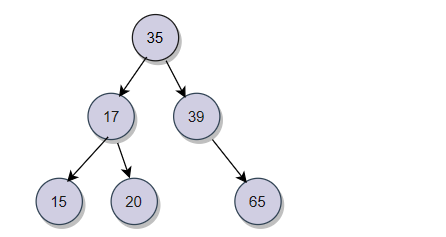
任何一颗树,左子树都要比根小,右子树都要比根大。搜索二叉树的这个特性使得它的插入位置就可以确定。例如我们要插入一个数据38:

从根开始,38比35大,就进入右子树,38比39小,那就插入到39左子树的位置。
例如我们再插入一个40:
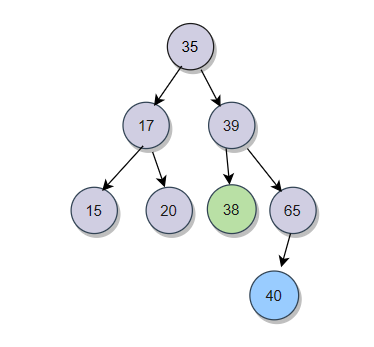
从根开始,40比35大,就进入右子树,40比39大,进入右子树,40比65小,那就插入到65的左孩子节点位置。
如果我们要查找一个数,例如我们查找30,30比35小,进入左子树,30比17大,进入右子树,30比20大继续进入到右子树,但20没有子节点,所以没有30这个节点,到这里就停止寻找。通过这些例子我们可以发现,这样的二叉树很适合搜索。搜索二叉树最多搜索高度次。
搜索的时间复杂度是O(N),细心的同学可能就会发现,搜素二叉树最多搜素高度次,那二叉树的高度不是有一个公式h= log₂(n+1),时间复杂度为什么不是O(log N)?
这里注意:这个二叉树的高度公式针对的是满二叉树,而搜素二叉树它可能出现退化的情况。如下图:
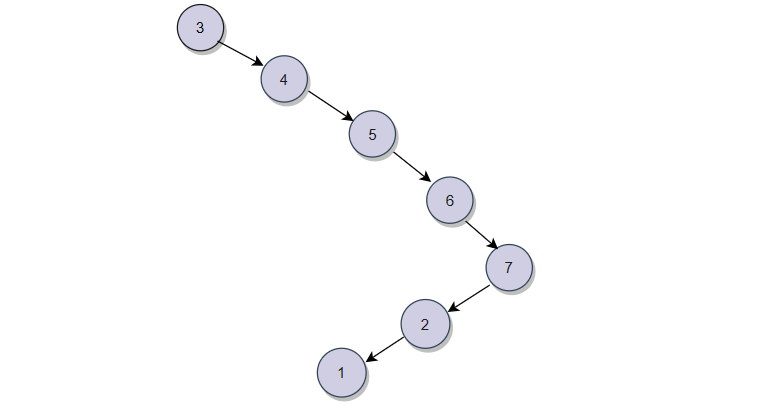
最坏的情况:我们找1这个节点,它的时间复杂度就是O(N)。
那要如何避免这种情况的发生?使左右两边的节点数量均匀,又要保持这个特性。
这里又可以引出一个新的概念——平衡树
平衡树的特性就是:左右两边的节点数据比较均匀。
平衡树又可以分为:
- AVL树
- 红黑树
依照现在博客所讲的水平,想要学会这两种树是不可能的,除此之外后续我们还会学习B树,它是一种多叉搜索树。数据库的原理就与它有关。(此部分为了解)这部分的树状结构才是有用的东西,精髓就在这部分内容,这里我们后续会进行学习。
本期我们不会进行代码的编写介绍,我们要弄清楚二叉树的性质,以及延申部分。接下来就是练习部分,帮助大家理解掌握二叉树的性质。
3. 练习
📖 题目一
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为 ()
A、不存在这样的二叉树
B、200
C、198
D、199
✨题目解析:
度为2的节点有199个,根据二叉树的性质:n₀=n₂+1,度为0的节点个数等于度为2的节点个数+1。度为0的节点就为叶子节点。
正确答案:B
📖 题目二
2. 在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A、n
B、n+1
C、n-1
D、n/2
✨题目解析:
这道题目看似无解,突破口就在完全二叉树。我们设度为0的节点个数为N0,度为1的节点个数为N1,度为2的节点个数为N2。根据性质可知:N0=N2+1,且N0+N1+N2=2n。
两式联合:N0+N1+N0-1=2n。
又因为这是一颗完全二叉树,完全二叉树度为1的节点只能有1个或没有。但又要确保都为整数,所以度为1的节点就只要1个。即:N0+1+N0-1=2n
正确答案:A
📖 题目三
3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A、11
B、10
C、8
D、12
✨题目解析:
题目要求这棵树的高度,那就设树的高度为h,最后一层缺了X个,根据定义我们可知:满二叉树是一种特殊的完全二叉树。
由此可得出:2^h-1-X就是完全二叉树的节点个数,即:2^h-1-X=531。到这里看似无解,但我们还可以根据性质进行推算,X的取值范围是0 ~ 2^(h-1)-1,至少最后一层有1个节点,最多最后一次为满(满二叉树),知道这些我们就可以带选项进行推算了。代换:2^h-1-2^(h-1)+1。代入选项,看最终哪个选项的结果最接近500。
代入11,2的11次方:2048-1024=1024,如果高度是11那最少有1024个节点,A选项错误。这样依次代入。
正确答案:B
总结
通过本篇博客我们对二叉树的内在结构、特性,有了更全面的了解,希望通过本篇博客的阅读,你已经掌握了深入理解二叉树的关键知识。最后,感谢阅读!
![[RDMA] 高性能异步的消息传递和RPC :Accelio](https://img-blog.csdnimg.cn/img_convert/13c2ab4b266e20d9af2fb2b17866dd8d.webp?x-oss-process=image/format,png)