圆方树

一些概念

割点：无向图中，若删除点x及其连边，连通块变多，那么x为割点。

点双连通：若点对x和y,删除任意非x和非y节点后，x和y仍然联通，称x和y点双连通。

点双联通子图：无向图中的一个子图G，G中任意两点都是点双连通的，那么G为原图的一个点双连通子图。

点双联通分量：无向图中的极大点双联通子图称为点双联通分量（V-DCC）

tips:点双联通不具有传递性，边双连通具有传递性

性质

• 1.无向图至少有三个点，才可能有割点（根据割点的定义）

• 2.dfs搜索树中的根结点有两个及以上的子节点是，才可能是割点

• 3.一个割点可能在多个点双中

正片

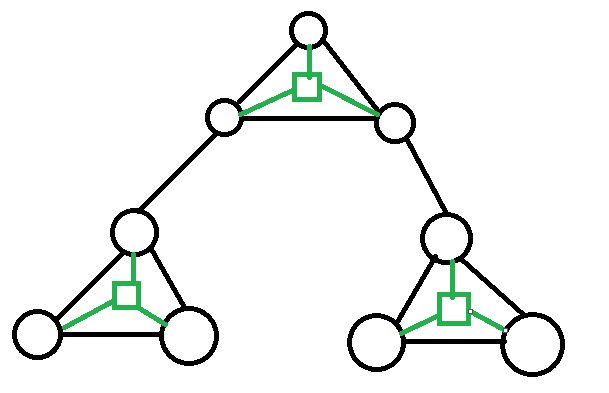
圆方树：将无向图转化为树形结构，解决"必经点"问题的数据结构

目标：构建一棵树，树上两点路径上的点都是原图的必经点

圆点：原无向图G中的点，仍然保留在圆方树中，称之为圆点

方点：将每一个点双连通分量新建一个方点

树边：每个方点向对应的点双内的圆点连边

下图为一棵圆方树的构建过程：

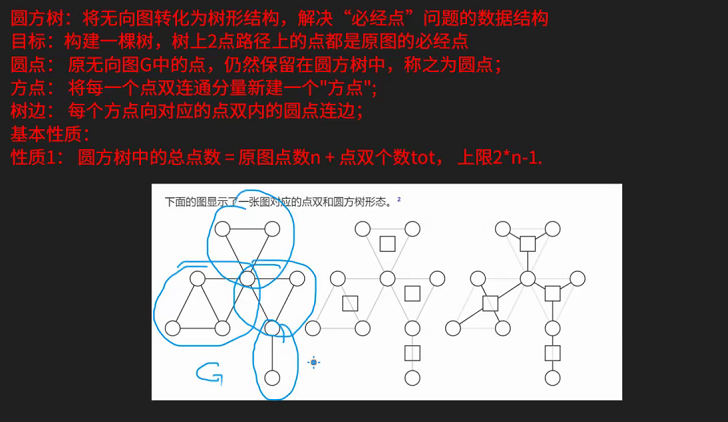
性质：

• 1.圆方树中的总点数=原图点数n+点双个数tot，上限为\(2\times n-1\)

• 2.圆点是被方点隔开的，一条边的两个端点一定是圆点和方点（所以显然这是一棵树）

• 3.圆点的度数就是包含该点的点双个数

• 4.圆方树删除点x后剩余节点的连通性与原图中删除x后的连通性等价

• 5.原图中x到y的路径的必经点就是圆方树上x到y经过的圆点

• 6.圆点为割点时才有超过一个儿子节点