长链剖分笔记

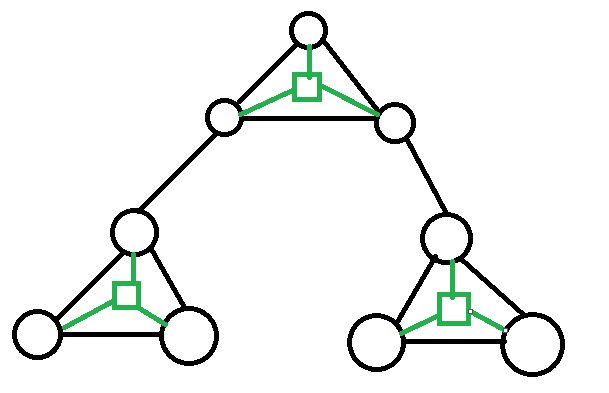
与轻重链剖分相似.

dfs1：高度 \(h\)、\(son\)；dfs2：\(top\).

性质 1：到根最多 \(O(\sqrt n)\) 条轻边. （证明：长链长度最坏情况：1, 2, 3...）

性质 2：\(x\) 的 \(k\) 级祖先 \(y\) 所在的长链长度 \(\ge k\).（证明：若非，则 \(y-x\) 是一条更长的链，矛盾.）

树上 \(k\) 级祖先 \(O(n\log n)-O(1)\)：每个点 \(i\) 处理倍增跳祖先数组 \(f(i,j)\)，链顶 \(i\) 处理向下 \(h_i\) 个点（长链上）、向上 \(h_i\) 个点.

询问 \((x,k)\)：令 \(y=f(x,\log k)\)，问题转化为求 \(z=(y,k-2^{\log k})\)；\(z\) 一定在 \(top(y)\) 内存储，根据深度判 \(z\) 是 \(top(y)\) 的祖先 / 后代. 就 \(O(1)\) 了.（性质 2 易证）

优化树上以深度为状态的 dp：套路：继承重儿子，合并轻儿子. 复杂度要为长链长度之和相关 \(=O(n)\).

Q：为什么不用轻重链剖分像这样优化 dp？

A：因为长剖使对于每个点 \(u\) 按这样算出来的 dp 数组的深度维总是达到了子树高度的上限、是对的，而重剖不一定，这样正确性就假了；且重剖不一定满足从每个点往上跳，链长总是递增的.

什么？你要例子？比如说这个：

例题，分散放其他地方。