【笔记】圆方树
1 定义
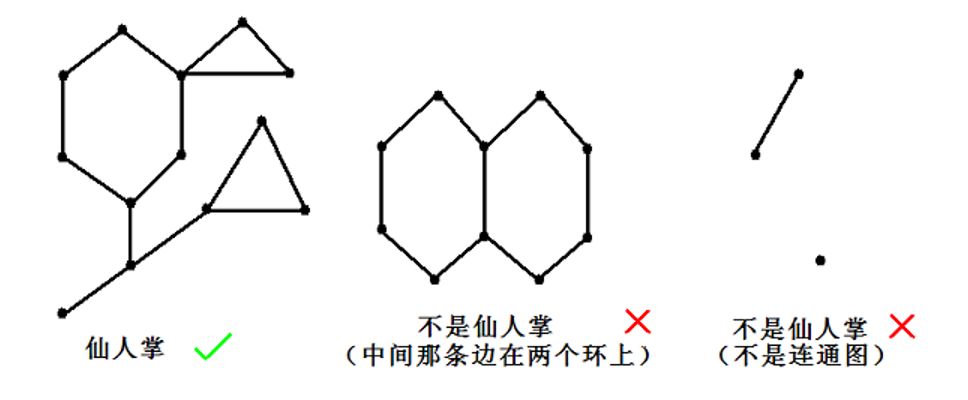
仙人掌: 所有边都至多被包含在一个环中。
2 构建
给一个点和它所在的所在的所有点双连边,同时,我们定义方点为虚点(即表示点双的点),圆点为原图上的点。
注意,是所有点双,所以一个割点会连向多个点双。同时,由定义得,该图有且仅有圆方边,因为圆圆边可以继续缩点。
既然是点双,那么我们就用 tarjan 实现即可。同时,在图不连通的时候,构成的是圆方森林,此时每一个连通子图就是一个圆方树,所以我们就考虑原图的连通子图即可。
然后呢,类似地,我们可以像求强联通分量一样,选择一个代表结点,作为此时的代表结点。对于这个点双连通分量的缩点,我们可以容易发现此时 u 即为这个点双联通分量的代表点,并且 u 和 v 属于同一个点双联通分量。
2.1 广义
广义圆方树的一个性质:所有的圆点的父亲一定是方点。
void tarjan (int u) {st.push(u), low[u] = dfn[u] = ++_dfn;for (int v : G[u])if (!dfn[v]) {tarjan(v);low[u] = min(low[u], low[v]);if (low[v] >= dfn[u]) {++_id; static int t;while (t != v) // 这个地方 do-while 或 while 都可t = st.top(), st.pop(),tr[_id].push_back(t),tr[t].push_back(_id);tr[_id].push_back(u),tr[u].push_back(_id);}} elselow[u] = min(low[u], dfn[v]);
}
2.2 狭义