EtherCAT总线耦合器:在Codesys和Twincat软件里组态案例
EtherCAT总线耦合器作为网络接口,连接主控制器(如PLC)和其他EtherCAT设备,实现实时、高效的数据交换。它能够支持工业自动化系统中的监控和控制功能,确保数据的准确性和实时性。

一、在欧姆龙Sysmac Studio软件中配置EtherCAT总线耦合器的步骤通常涉及多个环节,以下是操作步骤:

1、新建PLC项目
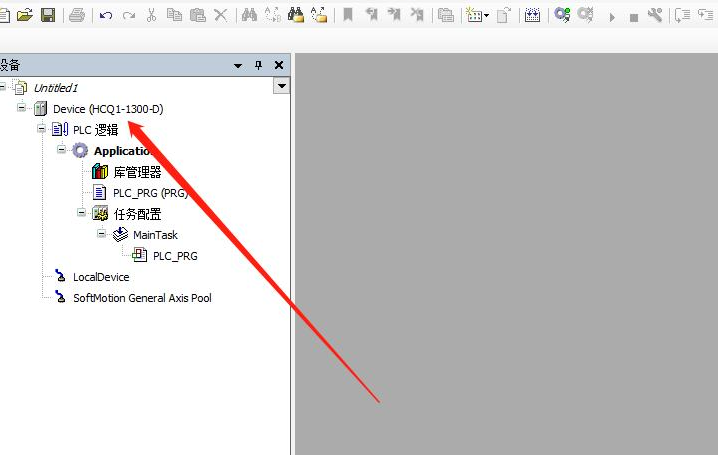
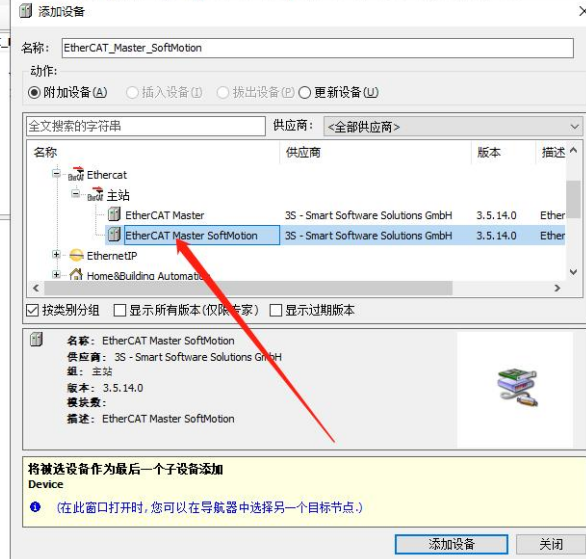
2、右键Deviec添加现场总线主站
3.添加localethercatDive
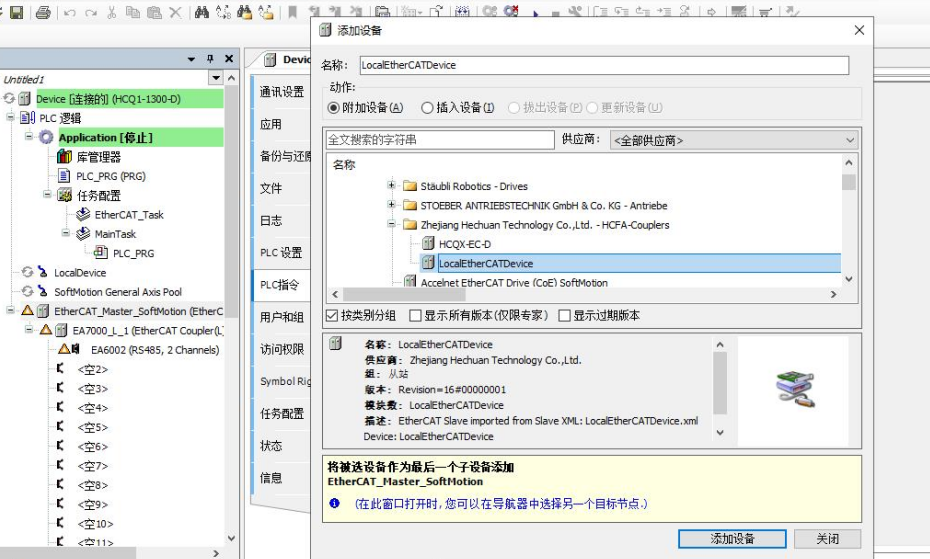
4、工具-设备存储库-安装-xml文件
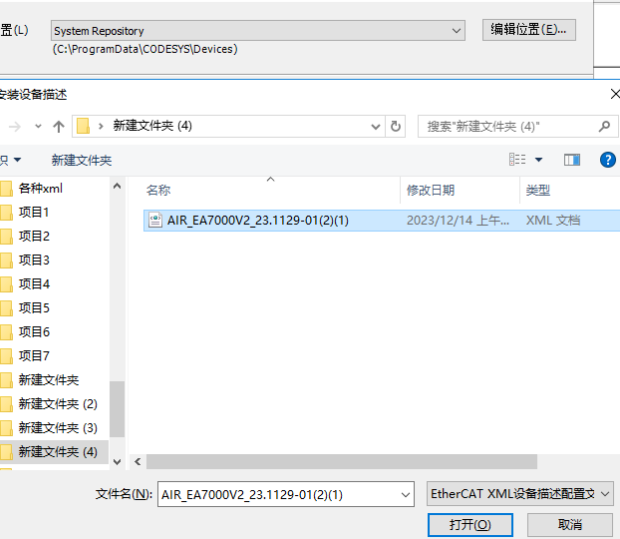
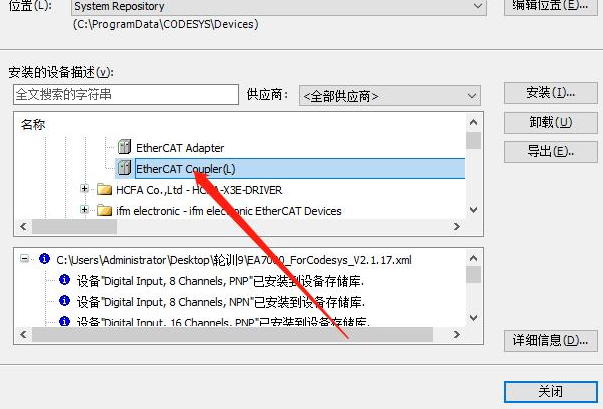
5.添加成功
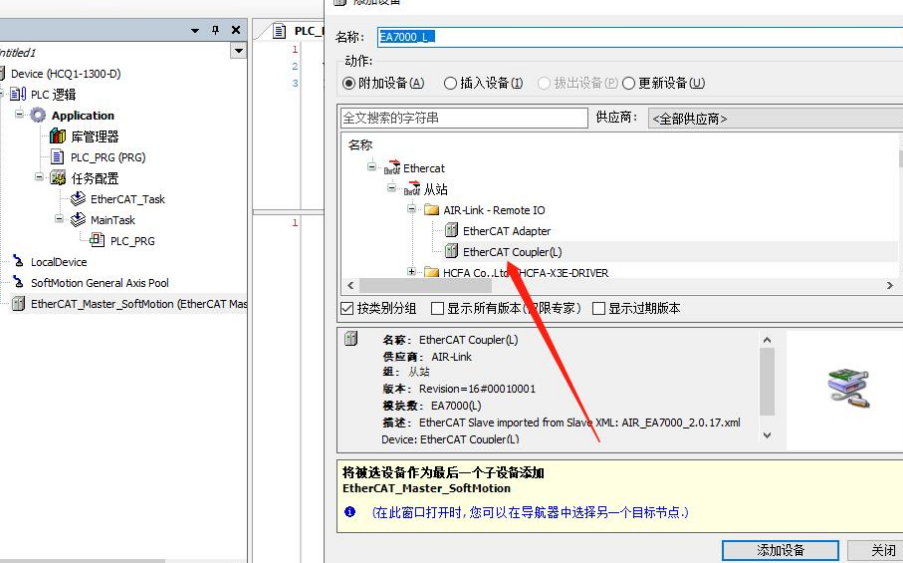
6.添加从站:右键点击ethercat主站-添加设备
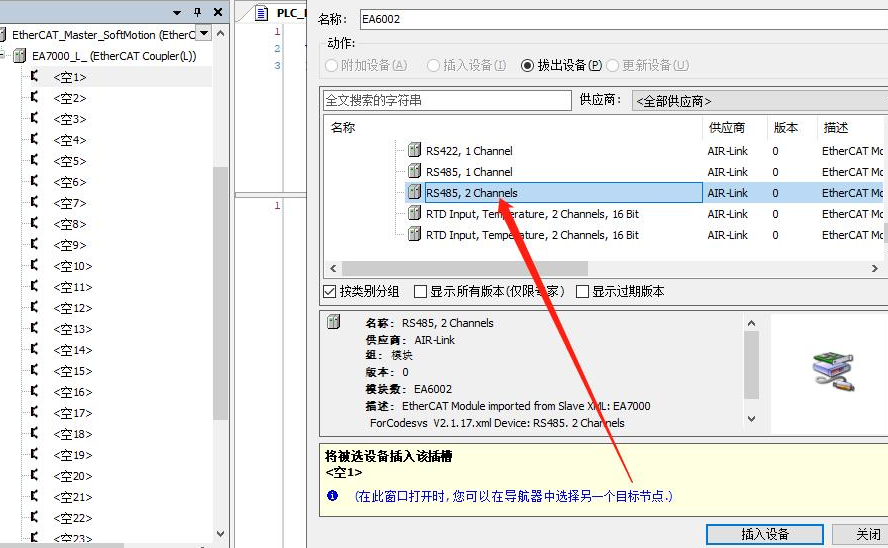
7.右键空1-插入设备找到配置的IO
8.登录-启动
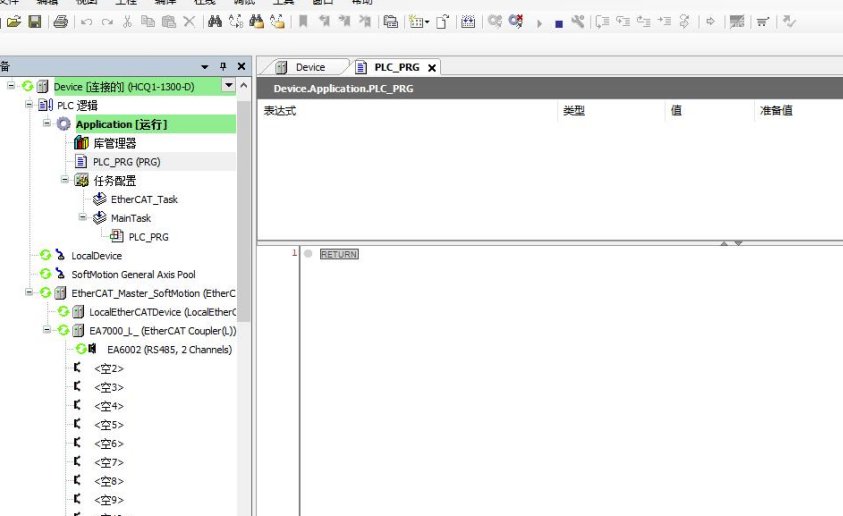
9、完成配置
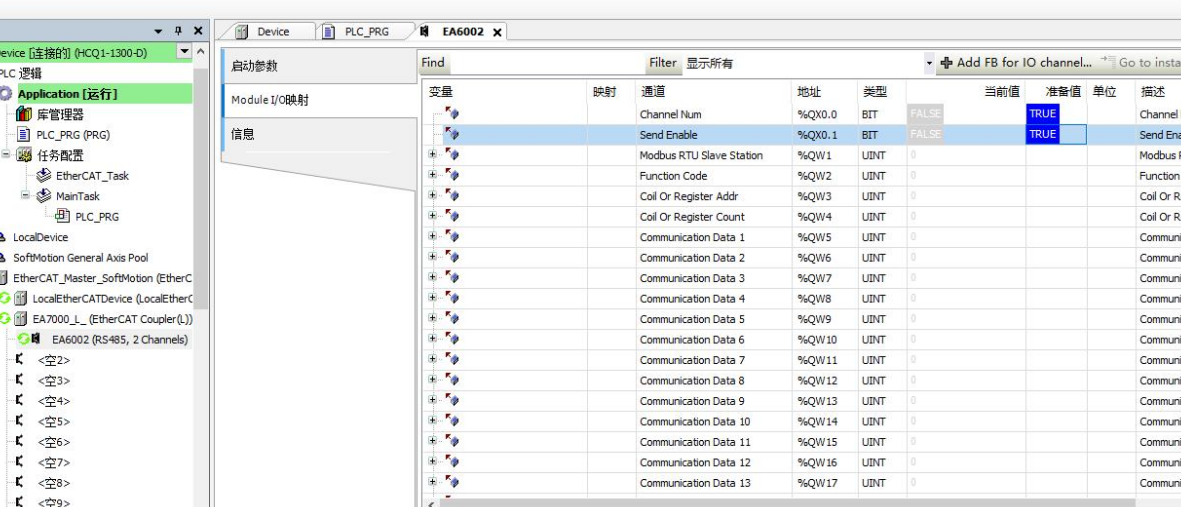
10、配置参数方法
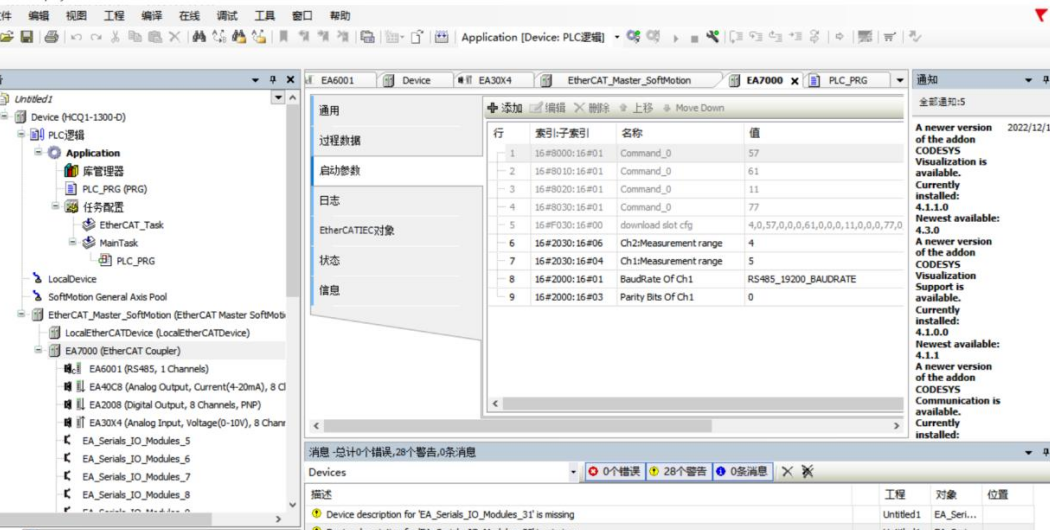
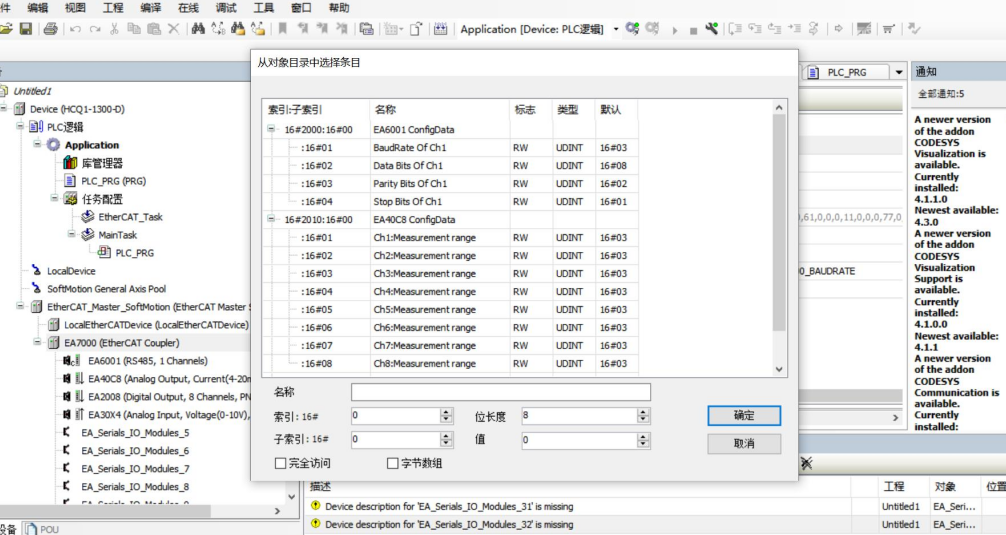
通过EtherCAT总线耦合器通过高效连接实现了不同机器人或自动化设备之间的高速通信。其通过自动检测和确定不同的设备连接方式,实现快速、直接和无缝连接,并保证高速数据传输。在应用领域具有广泛的适应性,安装简单,集成应用后可节省不少安装和设计成本。为机器人生产企业和自动化设备行业提供了可靠的技术支持。
 远程IO模块:EtherCAT总线耦合器XD7000实现工业自动化中主控制器与设备间实时数据交换,支持监控和控制功能。配置涉及多个步骤,确保数据准确性和实时性。其高速通信、无缝连接和广泛适应性为机器人和自动化设备行业提供可靠技术支持。
远程IO模块:EtherCAT总线耦合器XD7000实现工业自动化中主控制器与设备间实时数据交换,支持监控和控制功能。配置涉及多个步骤,确保数据准确性和实时性。其高速通信、无缝连接和广泛适应性为机器人和自动化设备行业提供可靠技术支持。
![[题解]POJ3675 Telescope——求多边形与圆相交部分的面积](https://img2024.cnblogs.com/blog/3322276/202407/3322276-20240717172407971-881168833.png)