目录
题目:
示例:
分析:
代码:
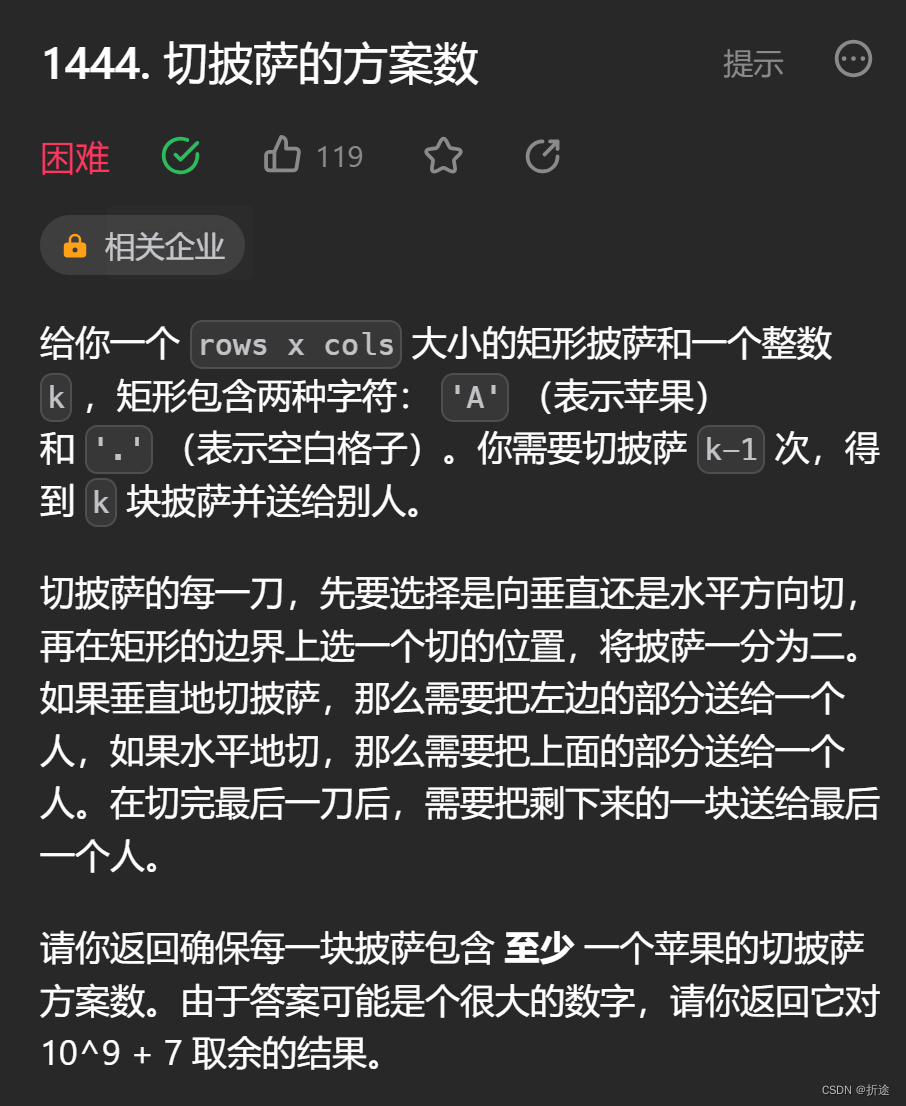
题目:
示例:

分析:
题目给我们一个二维数组来表示一个披萨,其中‘A’表示披萨上的苹果。
让我们切k-1刀,把披萨切成 k 份,只能横切或是竖切,最终 k 块披萨都需要拥有有苹果。
问我们一共有几种切披萨的方案。
我的第一反应就是递归去尝试,不过题目有说答案可能会很大,要取余1000000007,那么递归肯定是会超时的,所以我们应该使用动态规划。
因为每次切完披萨,送出去的不是左半边就是上半边,也就是说,披萨的右下角是会一直留下的。因此突破口应该在披萨的右下角,也就是矩阵的右下角。
题目要求每块披萨都需要有至少一个苹果,那么我们就应该要单独去统计一下苹果的分布情况,因为披萨的右下角是会一直留下来的,因此我们可以用一个二维矩阵来存放苹果的分布情况,这个矩阵坐标为 [ i , j ] 的元素就是披萨中 [ i , j ] 位置的右下角中拥有的苹果数。
那么我们初始化这个苹果分布情况数组的时候就应该从右下角开始统计,也就是利用前缀和去统计,递推公式如下,可以参考动图。
apple[i][j] += apple[i+1][j] + apple[i][j+1] - apple[i+1][j+1];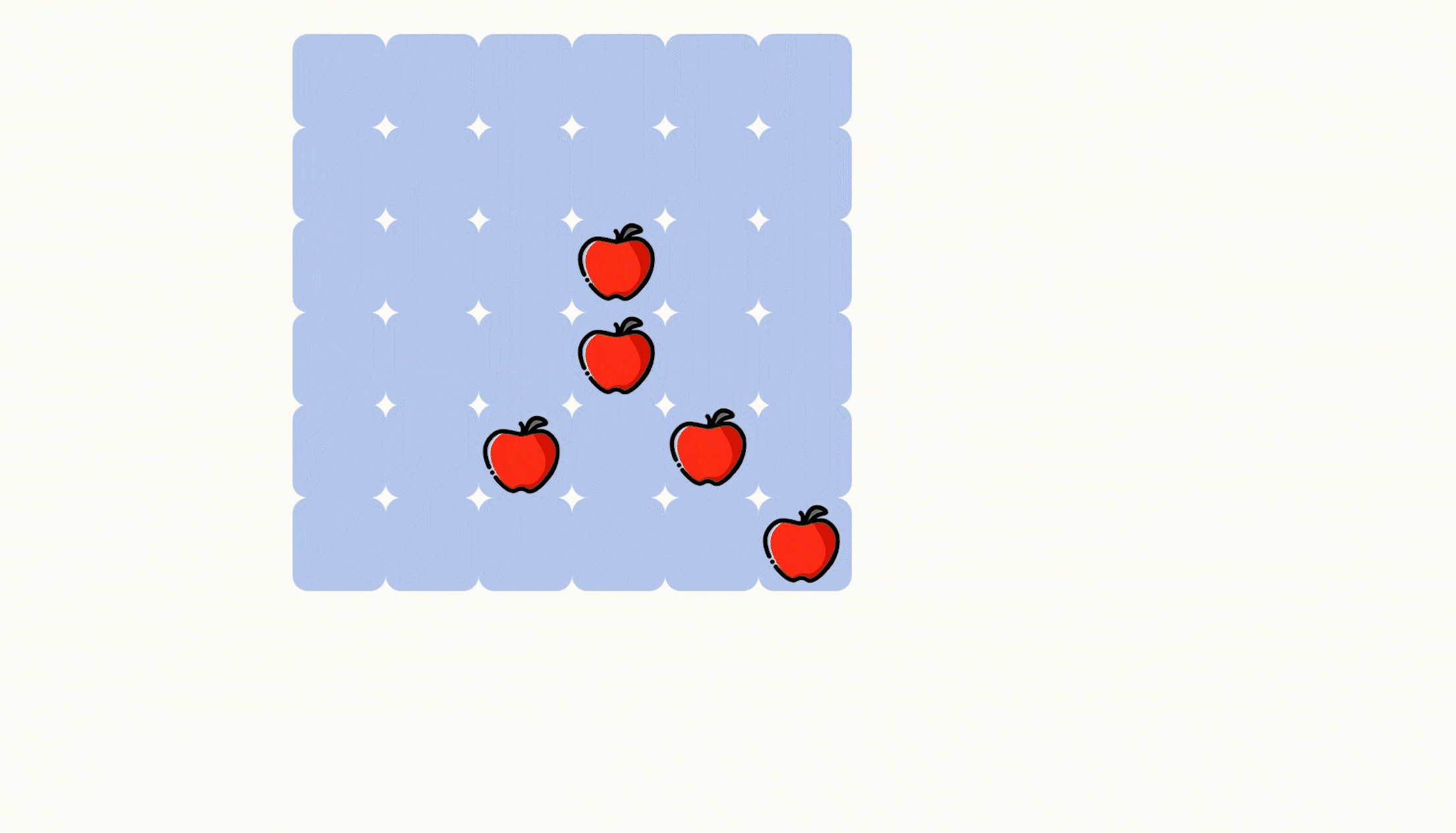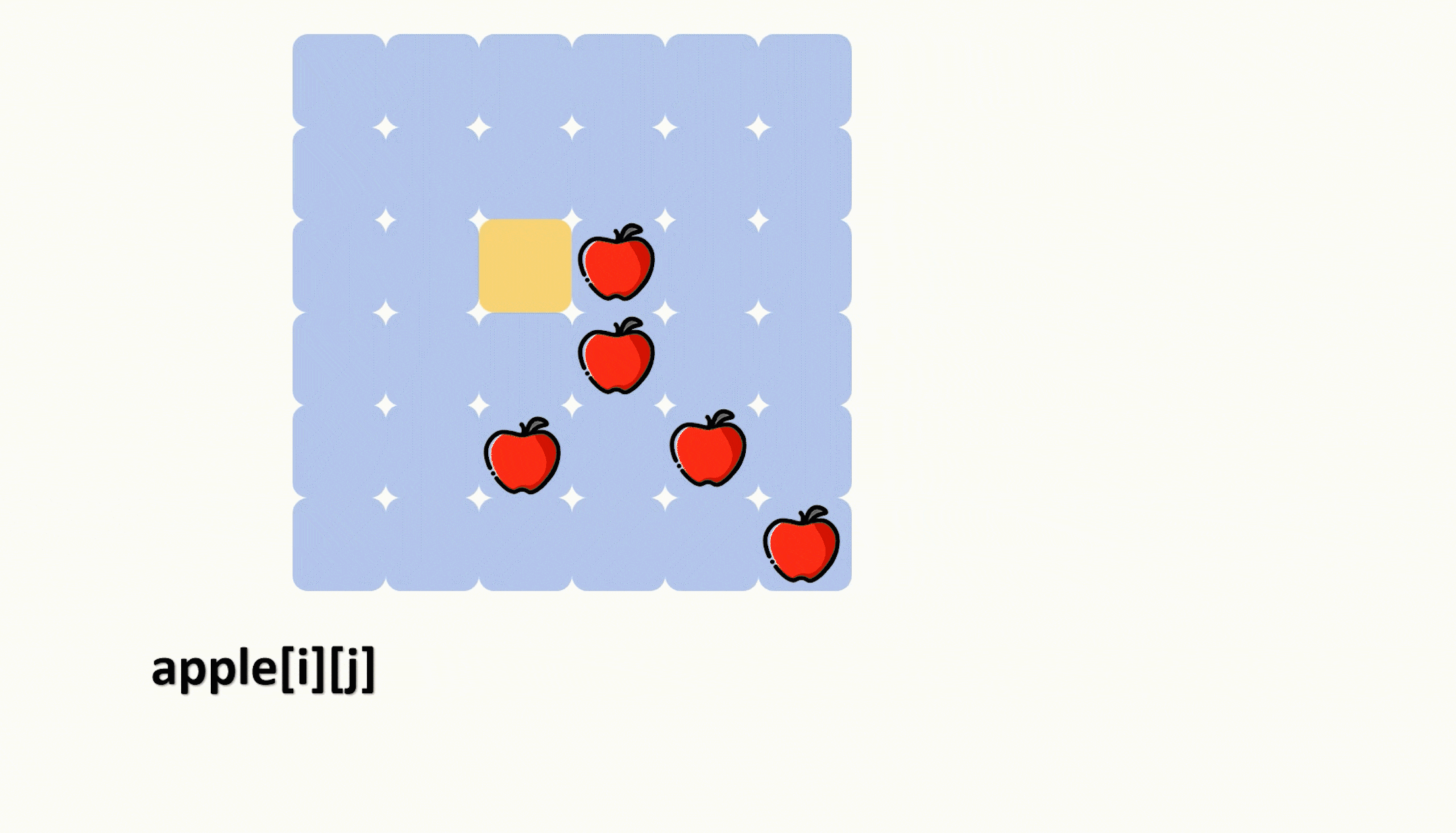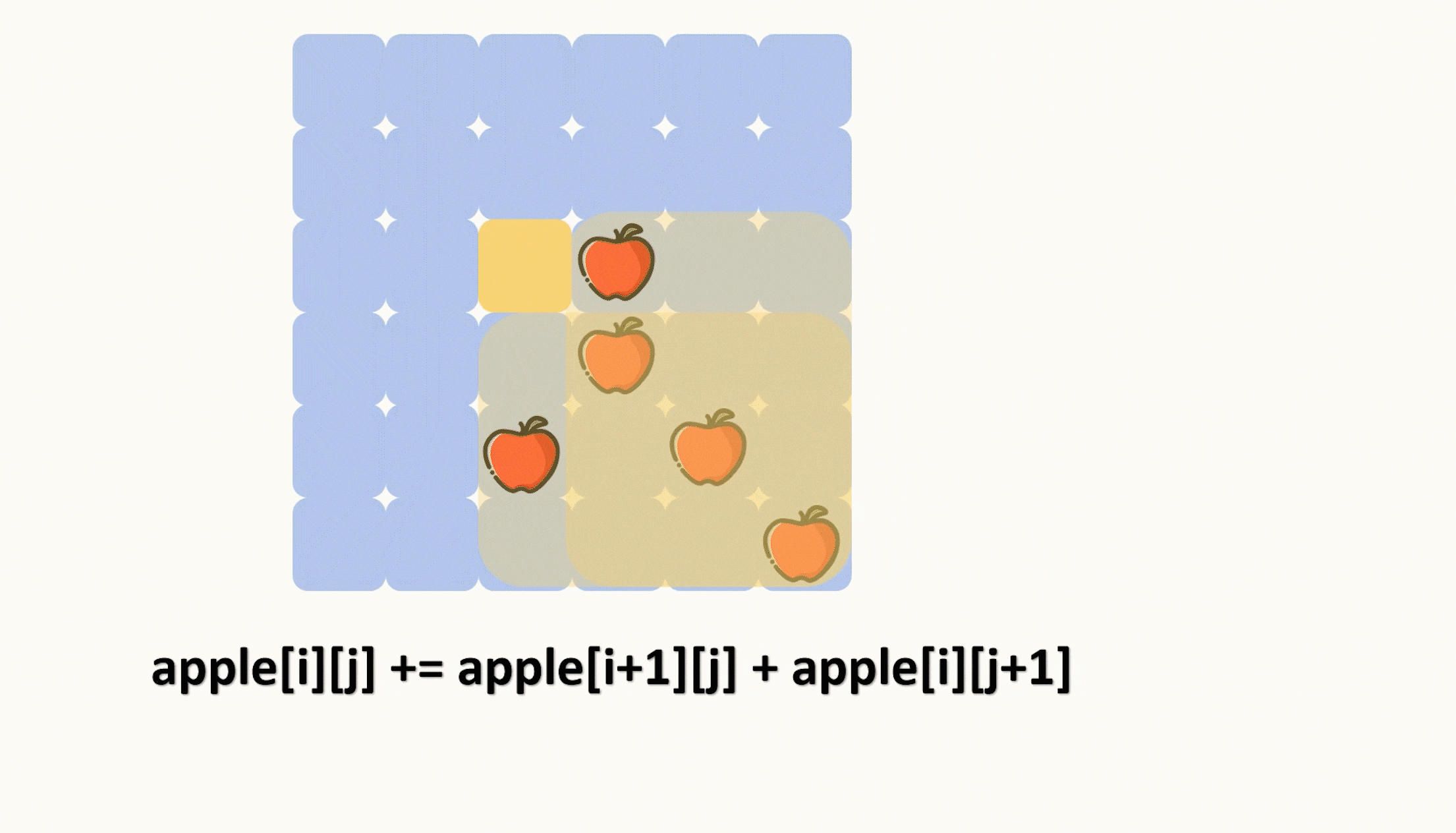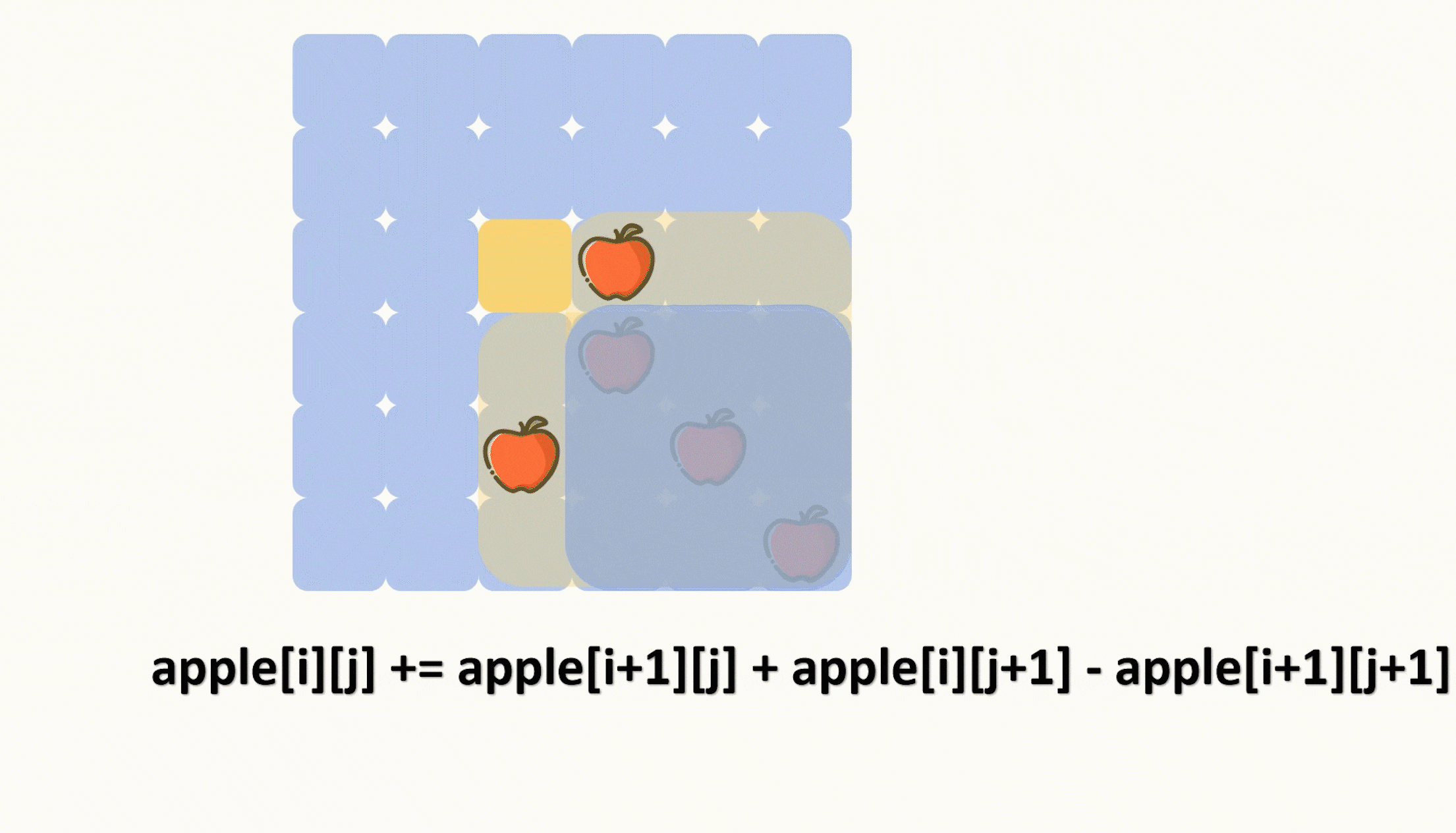
那么统计完了苹果的分布情况有什么用呢,因为要求每次切的披萨都要有苹果,那么我们可以用
apple[i][j1] - apple[i][j2]知道如果竖切的话,从 j1 到 j2 有没有苹果。用
apple[i1][j] - apple[i2][j]知道如果横切的话,从 i1 到 i2 有没有苹果。
解决完苹果的问题之后,我们就需要解决切披萨的方案数这个问题了。
由于固定是要切k-1刀,并且本身存放披萨就需要二维数组,因此我们的dp数组就是需要三维。
首先我们先定义dp数组的含义,dp[ i , j , k ]的含义是披萨仅剩从坐标 i , j 开始的右下角部分,并且可以切k刀的方案数。
由于我们可以横切也可以竖切,所以递推公式有两种:
//横切
dp[i1][j][z] += dp[i2][j][z-1]
//竖切
dp[i][j1][z] += dp[i][j2][z-1]也就是如果是横切的话,我在 i1,j 的位置可以切 z 刀的方案数就等于原本就可以切 z 刀的方案数再加上我一刀切在 i2 ,j 位置上,然后加上 i2,j 这个位置可以切 z - 1 刀的方案数。竖切也是同理。
并且我们刚刚说过了,披萨的右下角是保持不变的,所以我们应该从披萨的右下角开始递推,而刀数是从1开始的,所以刀数从小到大遍历。
最终填完dp数组之后,根据dp数组的含义,我们返回dp[ 0 , 0 , k-1 ] ,意思就是在披萨[ 0 , 0 ]的位置,我们可以切k-1刀的数目,也就是题目要我们返回的答案。
初始化的话我们依次对披萨的每个位置进行判断,如果对应的位置的右下角有苹果的话,那么一刀不切也是可以算一种方案的,也就是
dp[i][j][0] = 1最后要注意的就是由于答案会很大,因此每次递推我们都最结果进去取余处理。
代码:
class Solution {
public:int ways(vector<string>& pizza, int k) {int m = pizza.size(),n = pizza[0].size();vector<vector<int>>apple(m,vector<int>(n,0)); // i,j表示坐标为i,j的右下方的苹果数量for (int i = m-1; i >= 0; --i){for (int j = n-1; j >= 0; --j){if (pizza[i][j] == 'A') apple[i][j]=1;if (i == m-1 && j == n-1) continue; //防止越界提前退出.else if (j == n-1) apple[i][j] += apple[i+1][j]; //防止y轴越界else if (i == m-1) apple[i][j] += apple[i][j+1]; //防止x轴越界// 需要加上两部分并且删除重复计算的部分else apple[i][j] += apple[i+1][j] + apple[i][j+1] - apple[i+1][j+1];}}//dp[i,j,k]的含义是披萨仅剩从坐标i,j开始的右下角部分,并且可以切k刀的方案数vector<vector<vector<int>>>dp(m,vector<vector<int>>(n,vector<int>(k,0)));for (int i = m-1; i >= 0; --i){for (int j = n-1; j >= 0; --j){ if (apple[i][j] > 0) dp[i][j][0] = 1; //有苹果的话不切也是一种办法for (int z = 1; z < k; ++z){for (int y = i+1; y <= m-1; ++y){ //横切 if (apple[i][j] - apple[y][j] > 0) { //切出去上面的披萨的至少有一个苹果dp[i][j][z] = (dp[i][j][z] + dp[y][j][z-1])%1000000007;}} for (int x = j+1; x <= n-1; ++x){ //竖切if (apple[i][j] - apple[i][x] > 0){ //切出去左边的披萨至少有一个苹果dp[i][j][z] = (dp[i][j][z] + dp[i][x][z-1])%1000000007;}}}}}return dp[0][0][k-1] % 1000000007;}
};