2.2-2.9做题笔记

2.2 - 2.9 做题笔记

最近一周做的所有题目，包括 cyezoj 上的模拟赛，专题作业和 ABC。

2.4 CYEZ SHOI2025 模拟测试七

CYEZ 404 过桥

题目难度：省选 D1T1

赛时：20pts ；订正：100pts

大意

有 \(n\) 个人要过一座每次最多容 \(c\) 人通过、且仅有一只手电的一座桥。多人同时过桥的时间等于组内最慢者的时间。求所有人安全过桥的最小总时间。

做法

将所有人的过桥时间排序，定义 \(f_{i,j}\) 表示前 \(i\) 个人分成 \(j\) 组的最小时间，更新 dp 数组，计算每组的最小时间。

最终结果为 \(dp_{n,k-1-i} + v_i\) 的最小值。

初始化 \(f_{0,k} = 0\)，其中 $ k = \lceil \frac{n}{c} \rceil $，表示没有人过桥时的初始状态。

状态转移：

• 遍历每个人 \(i\) 和每组人数 \(j\)。
• 对于每个 \(i\) 和 \(j\)，如果 \(f_{i,j}\) 小于 INF，则尝试将接下来的 \(c\) 个人分成一组，更新 \(f\)。
• 对于每个 \(x\) 从 \(\min(n, i+c)\) 到 \(i\)，计算 \(f_{x,j+y}\) 的最小值，其中 \(y\) 表示增加的组数。

使用一个辅助数组 \(sum\)，其中 \(sum_i\) 表示前 \(i\) 个人的总时间。

最终结果为 \(f_{n,k-1-i} + v_i\) 的最小值，其中 \(v_i\) 表示前 \(i\) 个人的最小时间。

反思

赛时写了 \(c=2\) 的贪心，获得了 20pts，一直都在想时间复杂度正确的贪心，但全都假了，所以写了一个状压 dp。

自己对 dp 的运用还不够熟练，没有办法想到正确的状态设计，导致无法做到正解，应该多做一些综合性较强的动态规划。

比赛的时候也花了太多的时间想贪心，但是这道题的贪心显然是不可行的，自己还需要提升选择合适算法的能力。

CYEZ 405 蒙德里安的噩梦

题目难度： 省选 D2T2

赛时：15pts ；订正：15pts

大意

在已由一圈骨牌覆盖好边缘的 \(n \times m\) 棋盘中，用 \(1\times2\) 的骨牌覆盖剩余区域，要求覆盖无重叠且每个位置都被覆盖，同时不允许两块骨牌短边直接相邻拼接。最后输出方案数对 \(998244353\) 的取模结果。

反思

考场上写了 dfs 爆搜，加了一些剪枝，可以比不加剪枝的暴力多拿 15 pts，正解暂时还没有看懂。

对于这种难题，考场上一定要尽量拿一些部分分，尽量保证每道题都有分数。

CYEZ 406 转换

题目难度：省选 D2T3

赛时：0pts ；订正：10pts

大意

在最多 15000 次操作内，将第一棵仙人掌图转换成第二棵仙人掌图。

每次操作包括：从当前仙人掌中删除一条边，然后添加一条不存在的边，确保操作后图仍然满足仙人掌的定义（即每条边最多只出现在一个简单回路中，且无自环和重边）。

反思

这道题的 10pts 其实是可以尝试写的，但是考场上花了太多的时间想 T1，来不及写。

如果考试时一道题想不出来，就应该每道题都写一下部分分。

2.8 CYEZ SHOI2025模拟测试九

CYEZ 438 弹性碰撞

题目难度：省选 D1T1

赛时：10pts ； 订正：100pts

大意

在数轴上有 \(n\) 个小球，初始属性均为 \((A)\)。小球电荷有正负两种，部分已知，未知的可以任取。

给定初速度（正电向左、负电向右），小球间碰撞时会交换方向并交换电性与属性。经过足够长时间后，左侧收集到的 \((B)\) 小球数量作为摆放方式的权值。题目要求枚举所有合法电荷配置方案，求所有方案权值之和，结果对 \(998244353\) 取模。

做法

利用碰撞后电性反转的性质，推导出只有最左边的 \(k\) 个正电球能被收集，而且它们经过碰撞后其类型也固定（正电最终为 \(A\)，负电最终为 \(B\)）。

将问题转化为组合计数问题：预处理组合数和后缀和，枚举每个电荷是否贡献（要求该位置为负或问号，且序列中负电数量满足一定条件），从而在 \(O(n)\) 内求出所有合法电荷配置下收集的 \((B)\) 小球总贡献，对 \(998244353\) 取模。

反思

考场上一直在尝试写 \(O(n)\) 的模拟，但是没有想出来，就一直卡住了，根本没有想 \(O(n)\) 的组合数做法。

CYEZ 440 树上二位偏序问题

题目难度：省选 D1T3

赛时：10pts；订正：20pts

大意

给出一棵以 \(1\) 为根的 \(n\) 个节点的树，每个节点的权值来自 \({0,1,?}\)，其中问号可以替换为 \(0\) 或 \(1\)。对于任意一对满足 \(i\) 是 \(j\) 的祖先且 \(a_i < a_j\) 的节点，计为贡献 \(1\)。题目要求在所有问号取值后，求出能够获得的最大总贡献和，同时支持 \(q\) 次节点权值的修改，每次修改后输出当前树的最大贡献和。

反思

考场上只写了基础的暴力，菊花图的部分分比暴力还要好写，考场上没有来得及写，还是第一题花了太多时间，时间分配的问题。

平衡树专题练习

P3369 【模板】普通平衡树

题目难度：提高+/省选−

大意

设计一个数据结构来动态维护一个可重复的集合 \(M\)，并支持以下操作：

1. 插入一个元素 \(x\)；
2. 删除集合中一个 \(x\)（如果有多个只删除一个）；
3. 查询集合中比 \(x\) 小的数的个数（结果加一输出）；
4. 查询集合中第 x$$ 小的数；
5. 查询 \(x\) 的前驱（集合中小于 \(x\) 的最大值）；
6. 查询 \(x\) 的后继（集合中大于 \(x\) 的最小值）。

做法

学习了 WBLT 写平衡树，利用随机化的 split 和 merge 操作实现插入和删除。通过维护每个节点的子树大小，实现以下操作：

1. 插入：根据值大小遍历找到插入位置，split 后 merge 新节点插入。
2. 删除：定位待删元素，利用 split 分离出该节点，再 merge 剩余部分。
3. 查询：
   • Rank 查询：累加左子树大小得到比目标小的元素数目。
   • kth 查询：以子树大小指导找到第 \(k\) 个元素。
   • 前驱/后继查询：在遍历过程中记录小于/大于目标值的最大/最小值。

时间复杂度为 O(log n)。

由于是模板，贴一下代码。

反思

只学模板显然是不够的，需要多做综合题，熟练运用，才真正有可能在考场上用出来。

然后就开始用 WBLT 做所有 FHQ Treap 的题

P3391 【模板】文艺平衡树

题目难度：提高+/省选−

大意

维护一个有序数列，并实现区间翻转操作。例如，给定序列 \(5\ 4\ 3\ 2\ 1\)，对区间 \([2,4]\) 翻转后，序列变为 \(5\ 2\ 3\ 4\ 1\)。

做法

众所周知，FHQ Treap 可以解决的问题 Leafy Tree 都可以做，所以我就用 WBLT 做了这道题。

对于每个翻转区间 \([l, r]\)，利用 split 分割出区间对应的子树，再将这一段的翻转标记置反（懒标记），最后使用 merge 将三部分合并回原树。

懒标记下传：在 push_down 中，当一个节点有翻转标记时，交换左右子树并将标记下传，从而延迟真正翻转操作。

通过随机化合并实现平衡，每次操作时间复杂度为 \(O(log n)\)。

通过中序遍历输出更新后的序列。

P5055 【模板】可持久化文艺平衡树

题目难度：省选/NOI−

大意

设计一个持久化平衡树，用于维护一个序列并支持以下操作：

1. 在历史版本中第 \(p\) 个数后插入一个数 \(x\)，生成新版本。
2. 在历史版本中删除第 \(p\) 个数，生成新版本。
3. 在历史版本中翻转区间 \([l, r]\)（例如 \({5,4,3,2,1}\) 翻转 \([2,4]\) 得到 \({5,2,3,4,1}\)），生成新版本。
4. 在历史版本中查询区间 \([l, r]\) 内所有数的和（查询操作不修改版本）。

每次操作均基于某个历史版本，通过复制节点实现持久化，使得新操作生成的版本编号为当前操作序号，同时保留历史版本。

做法

1. 利用“路径复制”策略，所有操作（插入、删除、区间翻转、区间求和）均基于某历史版本进行操作，同时复制修改路径上的节点，生成新版本。

2. 操作

   • 插入：先利用 split_size 将树按位置分割成两部分，再构造新节点，将其与两部分合并。
   • 删除：根据位置分割出要删除的节点，再合并剩余部分。
   • 区间翻转：利用 split_size 分离出区间子树，对该子树打上翻转标记，最后重新合并。
   • 查询区间和：利用 split_size 分割出目标区间，计算该区间总和，然后再将各部分合并恢复原状态。

3. 每次操作（除查询外）都会基于指定历史版本进行修改，生成新版本并更新版本数组；查询操作亦基于指定版本进行，并在查询后复制版本确保不改变原历史记录。

反思

平衡树的题暂时只做了这三道，显然是不够的，后面还要再练习一些平衡树与其他算法相结合的综合题。

图上随机游走专题练习

P3232 [HNOI2013] 游走

题目难度：省选/NOI−

大意

给定一个无向连通图，包含 \(n\) 个顶点和 \(m\) 条边。要求对这 \(m\) 条边进行编号（编号从 \(1\) 开始），使得从起点 \(1\) 到终点 \(n\) 进行随机游走时，所获得的分数期望最小。游走过程中，每一步从当前顶点等概率选择一条边前进，并获得该边编号作为分数，当到达顶点 \(n\) 时结束。

做法

对于非终点顶点 \(i\)，根据随机游走的性质建立等式，即通过传递关系构造线性方程组，系数由顶点的邻接关系和各顶点的度数确定。利用高斯消元求解得到每个顶点到终点的值。

对于每条边，其贡献值 \(f_i\) 由两端点的差乘以 \(\frac{1}{deg}\)）决定。简单来说，如果边的一个端点不是终点，则 \(f_i\) 累加该端点的贡献。这样每条边对应一个数值 \(f_i\)，反映了其在随机游走过程中对总分的影响。

为了最小化期望总分，应将编号分配给边，使得贡献较大的边编号较小。对 \(f\) 排序后，然后按照升序分配编号（编号从 \(1\) 到 \(m\)），使得贡献较小的边获得较大的编号，从而降低整体期望分数。

答案通过对 \(f\) 加权求和得到，每条边贡献乘以其 \(m-i+1\)，累加得到最终期望值。

反思

这道题和我之前的期望练习中的题目思路类似，通过列线性方程组用高斯消元求出每个点到中点的值再列式求期望。

P3211 [HNOI2011] XOR和路径

题目难度：省选/NOI−

大意

本题给定一个无向连通图（节点编号 \(1\) 到 \(N\)，边上有非负整数权值），要求求出使用随机游走算法得到的从 \(1\) 到 \(N\) 的路径的 XOR 和的期望值。

具体来说，从节点 \(1\) 开始，每步均以相等的概率选择一条与当前节点相连的边前进（自环和重边均允许），直到到达节点 \(N\) 为止；路径上每条边的权值参与 XOR 运算（如果一条边重复出现，则其权值也重复计入 XOR 运算）。

计算这种随机游走生成的路径的 XOR 和的期望值，并保留三位小数。

做法

遍历每一位（共 \(31\) 位），对每个位独立处理。对于位 \(b\)，如果一条边的权值在这一位为 \(1\)，则对状态转移有负面贡献（同时常数项减少）；否则为正面贡献。

对于每个非终点顶点 \(u\ (1 \leq u \le n)\)，根据随机游走的转移概率（即 \(\frac{1}{d_u}\)，\(d_u\) 为 \(u\) 的度数），构建对应的方程：

• 设 \(a_{u,u} = –1\)（左边齐次项）；
• 对于每条从 \(u\) 出发的邻边到达 \(v\)，根据该边 \(b\) 位的值更新 \(a_{u,v}\)（加上或减去 \(\frac{1}{d_u}\)）和常数项 \(a_{u}{n+1}\)。
  对于终点 \(n\)，设定 \(a_{n,n} = 1\)，常数项为 \(0\)，以保证终点的期望值为已知 \(0\)。

对构造的 \(n\) 元线性方程组进行高斯消元，求出从顶点 \(1\) 开始的解 \(f_1\)，即从起点出发该位对总期望贡献的值。

累加每一位的贡献：对位 \(b\)，将 \(f_1\) 乘以 \(2^b\) 加入最终答案 \(ans\)。

反思

我之前准备的专题概率期望是这个专题的基础，两者融会贯通了。

网络流专题练习

网络：网络是指一种特殊的有向图 \(G=(V,E)\)，存在容量和源汇点。

这里，我们记源点 \(s\)，汇点 \(t\)，边 \([u,v]\) 的容量为 \(c(u,v)\)。

可以想象一下，将有向图想象成一个庞大的水管系统，从一个端点倒水，水会从另外一个端点流出。

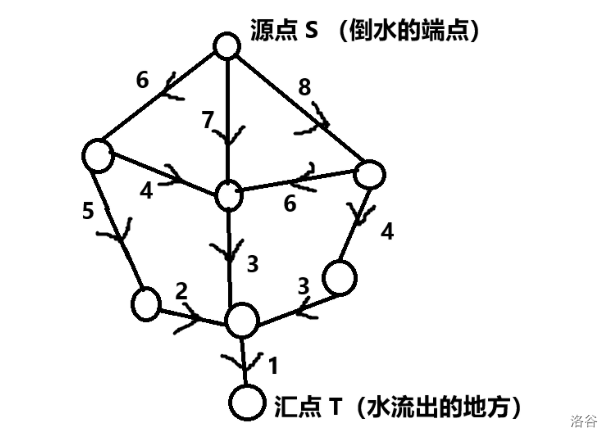
如图就是一张网络。（图丑勿喷）

流：对于一个网络 \(G=(V,E)\)，流是一个从边集 \(E\) 的整数集或实数集的函数（记流函数 \(f(u,v)\)），满足：

1. 对于每条边，流经该边的流量不得超过该边的容量：\(0\leq f(u,v) \leq c(u,v)\)。

2. 除了 \(s,t\) 之外，任意节点 \(u\) 的净流量为 \(0\)。

这里同样可以想象，将水从源点倒入，显然只有汇点可以有水流出，其他的点都必须将流入的水全部排出到其他节点，这就是流守恒性。同时，水管中流的水不可以比容量大，这就是容量限制。

割：对于一个网络 \(G=(V,E)\)，割是指将点集 \(V\) 分为两个集合 \(S\) 和 \(T\)，其中源点 \(s \in S\)，汇点 \(t \in T\)。割的容量定义为所有从 \(S\) 到 \(T\) 的边的容量之和。

形象地说，就是将网络中的一些水管直接切断，使得源点和汇点不再连通。切断的水管的容量之和就是割的容量。

以上的定义主要来自 oi-wiki，加上个人的理解。

P3376 【模板】网络最大流

题目难度：提高+/省选−

大意

求从源点 \(S\) 到汇点 \(T\) 的最大流量。

做法

Edmonds-Karp 算法 (EK 算法)

EK 算法是一种基于增广路的求解最大流的算法。它的核心思想是：每次寻找从源点到汇点的最短增广路，然后沿着增广路更新流量，直到找不到增广路为止。

1. 寻找增广路：使用 BFS 寻找从源点到汇点的最短增广路。
2. 更新流量：沿着增广路更新流量，正向边减去流量，反向边加上流量。
3. 重复步骤 1 和 2：直到找不到增广路为止。

时间复杂度：\(O(V \times E^2)\)，其中 \(V\) 是顶点数，\(E\) 是边数。

Dinic 算法

显然，EK 算法的时间复杂度是不够优秀的，每次都有可能遍历整个残量网络。

Dinic 算法是一种比 EK 算法更高效的最大流算法。通过分层图和多路增广提高效率。

1. 构造分层图：使用 BFS 构造从源点到各个顶点的分层图，记录每个顶点的层数。
2. 多路增广：从源点开始，沿着分层图进行多路增广，每次尽可能地增加流量。
3. 重复步骤 1 和 2：直到无法增广为止。

时间复杂度：\(O(V^2 E)\)，对于某些特殊图可以达到 \(O(V^2 \sqrt{E})\)。

当前弧优化：在每次增广时，记录每个顶点已经访问过的边，下次增广时从上次访问的边开始继续访问，避免重复访问已经访问过的边。

EK 代码；Dinic 代码；

P3381 【模板】最小费用最大流

题目难度：提高+/省选−

大意

每条边 \((u,v)\) 除了有容量 \(c(u,v)\) 之外，还有一个费用 \(cost(u,v)\)，表示单位流量流经该边所需要的费用。在保证最大流的前提下，求最小（或最大）的总费用。

做法

EK+SPFA 求费用流

EK 求最大流的过程就是通过 BFS 不断寻找增广路，每次找到一条之后更新，通过反向边进行反悔。

现在加入了费用的概念，不难联想到最短路算法。

此时会有一个大胆的想法：SPFA 和 Dij 都是基于 BFS 进行的，那么是不是只需要把 EK 中的 BFS 替换成 SPFA/Dij 就行了呢？

而前文提到求最大流一个很重要的步骤就是建立反向边反悔，而一条正向边的费用显然大于 \(0\)，而反向边为了能够正确地进行反悔，其费用就需要取正向边的相反数。

于是这个网络出现了负边，Dij ~~死~倒闭了。

那为什么把 BFS 换成 SPFA 求最小费用最大流就是对的呢？

• 如果两条边的流量相同，我们需要找到费用较小的那一条边，这一部分 SPFA 显然是对的。

• 如果流量较大的那条边费用较小，用最短路算法找增广路就一定会找到这条边，可以保证流量最大且费用最小。

• 如果流量较大的那条边费用较大，用最短路算法第一遍会找到费用较小的那条边，于是流量大的边成为了图中的一条增广路。按照 EK 的求解步骤，流量较大的边还是会被找到并更新。

因此就可以用 EK+SPFA 求最小费用最大流了！

EK+SPFA 代码

反思

网络流其实是必须掌握的知识点，但是种种原因之前一直没有学习，最近补一下，再做一些网络流建图的题目。

参考

P1646 [国家集训队] happiness

题目难度：省选/NOI−

模型：二元关系最小割模型

大意

有一个 \(n\times m\) 的同学矩阵，现在要分文理科，每个同学对于选择文科与理科有着自己的喜悦值。

而一对好朋友如果能同时选文科或者理科，那么他们又将收获一些喜悦值。

求最大喜悦总和。

做法

考虑每个同学必须选择文科/理科（废话），容易想到对这个矩阵建网络求最小割。

先建立一个源点 \(s\) 和一个汇点 \(t\)，每个同学都建一个点，共 \(n \times m + 2\) 个点。

对于第一种关系：同学选文科 or 理科的喜悦值，分别将该同学节点向 \(s\) 或 \(t\) 建边。

对于第二种关系：两个相邻的同学同选文科 or 理科的喜悦值，直接将这两个同学之间建边。

边权要怎么定？

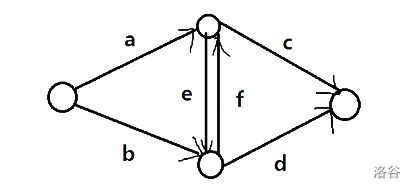
参照这张图，我们解方程。

首先令第 \(i\) 位同学选文科的喜悦值为 \(A_i\)；第 \(i\) 位同学选理科的喜悦值为 \(B_i\)；

第 \(i\) 和 \(j\) 位同学同选文科喜悦值为 \(C_{i,j}\)；第 \(i\) 和第 \(j\) 位同学同选理科的喜悦值为 \(D_{i,j}\)。

然后对于每个点对 \((i,j)\) 列出方程：（按照同文、同理、一文一理、一理一文的顺序）。

\( \begin{cases} c + d = B_i + B_i + D_{i,j} \ \ \ \ (1) \\ a + b = A_j + A_j + C_{i,j} \ \ \ \ (2) \\ b + c + e = B_i + A_j + C_{i,j} + D_{i,j} \ \ \ \ (3) \\ a + d + f = A_i + B_j + C_{i,j} + D_{i,j} \ \ \ \ (4) \\ \end{cases} \)

理解一下，这些边的贡献等于割掉这些边后会失去的贡献。

解方程：\((3)+(4)-(1)-(2)\) 得到 \(e+f=C_{i,j}+D_{i,j}\)。

\(e=f\)，所以 \(e=f=\frac{C_{i,j}+D_{i,j}}{2}\)

由于方程的解需要对称，注意到当 \(a=A_i+\frac {c_{i,j}}{2}\) 时，解得：

\( \begin{cases} a = A_i+\frac {c_{i,j}}{2} , b = A_j+\frac {c_{i,j}}{2} \\ \\ c = B_i+\frac {d_{i,j}}{2} , d = B_j+\frac {d_{i,j}}{2}\\ \end{cases} \)

根据这个方程建边，跑 Dinic 求出最小割，最后用总和减去最小割容量就是答案。

反思

这个专题最近还会继续练习，做题笔记在我的博客会一直更新。

Atcoder Beginner Contest 392

这是简单场，除了 E 都没吃罚，E 交了 6 发没过。。。

E 订正完之后会补一下笔记。

D - Doubles

题目难度：clist 603

大意

给定 \(N\) 个骰子，每个骰子有不同数量的面，每个面上写着一个数字。选择两个骰子，同时掷出，计算两个骰子出现相同数字的概率。目标是找到选择哪两个骰子能使这个概率最大，并输出这个最大的概率。

做法

注意到数据范围中有一条 \(K_1 + K_2 + \dots + K_N \leq 10^5\)。

考虑使用 unordered_map 统计每个骰子各数字出现的频率，遍历每个骰子对，计算相同数字出现的概率之和，取最大值就是答案。

F - Insert

题目难度：clist 1363

大意

给定一个空数组 \(A\)，依次进行 \(N\) 次插入操作。第 \(i\) 次操作将数字 \(i\) 插入到数组 \(A\) 的第 \(P_i\) 个位置（从 \(1\) 开始计数）。输出最终的数组 \(A\)。

做法

使用树状数组维护数组 \(A\) 的空位信息，快速找到插入位置。

对于插入操作： 每个 \(i\) 从 \(N\) 到 \(1\)，使用树状数组 findKth 操作，找到第 \(P_i\) 个空位在数组 \(A\) 中的位置 \(pos\)，将数字 \(i\) 插入到数组 \(A\) 的位置 \(pos\)，在树状数组中，将位置 \(pos\) 的值更新为 \(0\)，表示该位置已被占用。

时间复杂度为 \(O(N \times \log N)\)，空间复杂度为 \(O(N)\)。

G - Fine Triplets

题目难度：clist 1773

大意

给定一个包含 \(N\) 个不同正整数的集合 \(S\)。

如果三个整数 \(A, B, C (A < B < C)\) 满足 \(B - A = C - B\)，则称 \((A, B, C)\) 为一个“好三元组”。

求集合 \(S\) 中有多少个好三元组。

做法

利用 FFT 加速卷积运算，快速统计。

使用 FFT 计算数组 \(f\) 与自身的卷积，得到数组 \(conv\)。数组 \(conv\) 的第 \(i\) 个元素表示集合 \(S\) 中有多少对数字 \((x, y)\) 满足 \(x + y = i\)。

遍历集合 \(S\) 中的每个元素 \(b\)。

对于每个元素 \(b\)，计算 \(2 \times b\) 的值。

如果 \(2\times b\) 小于数组 \(conv\) 的大小，则 \(conv_{2\times b}\) 表示集合 \(S\) 中有多少对数字 \((x, y)\) 满足 \(x + y = 2\times b\)。

由于 \(x\) 和 \(y\) 可以相同，因此需要减去 \(1\)（即 \(x = y = b\) 的情况）。

由于 \((x, y)\) 和 \((y, x)\) 算作同一种情况，因此需要除以 \(2\)。

每次计算完之后将结果累加到 ans 中。

时间复杂度 \(O(m \times \log m)\)