雷达气象学（4）——雷达参数和雷达气象方程

目录

• 4.1 与脉冲相关的参数
  • 4.1.1 电磁波的波长
  • 4.1.2 脉冲重复频率（PRF）和脉冲重复周期（PRT）
  • 4.1.3 脉冲宽度和脉冲长度
  • 4.1.4 脉冲发射功率
• 4.2 与天线相关的参数
  • 4.2.1 天线方向图和波束宽度
  • 4.2.2 天线增益
• 4.3 雷达气象方程
  • 4.3.1 单个目标的雷达气象方程
  • 4.3.2 粒子群的雷达气象方程

本篇文章将介绍雷达的几个常用参数，并给大家看看“传说”中的雷达气象方程长什么样。

4.1 与脉冲相关的参数

4.1.1 电磁波的波长

雷达波长已经在《雷达的基本知识》那篇文章已经讲过了，指的是发射电磁波的波长，是雷达的主要参数之一，一般用 \(\lambda\) 表示。雷达波长直接影响雷达的探测性能和测速范围，如下表所示：

波段	波长	探测的气象目标	备注
K波段	0.75～2.4cm	各种不产生降水的云	最常用的是Ka波段
X波段	2.4～3.75cm	探测降水	作为新一代天气雷达网的补充
C波段	3.75～7.5cm	探测降水	一般安装在西部地区和内陆地区
S波段	7.5～15cm	探测降水，最适用于探测暴雨和冰雹	一般安装在中、东部多雨地区和沿海地区
L波段	15～30cm	探测晴空大气的风场	用于风廓线雷达

4.1.2 脉冲重复频率（PRF）和脉冲重复周期（PRT）

每秒钟产生的脉冲数目，称为脉冲重复频率（Pulse Repetition Frequency, PRF），单位为 Hz。相邻脉冲之间的间隔时间，称为脉冲重复周期（Pulse Repetition Frequency, PRT），单位为 s。显然两者是一个倒数关系，即：

\[\mathrm{PRF} = \frac{1}{\mathrm{PRT}} \]

脉冲周期确定了雷达的最大探测距离。这是因为，雷达是周期性地发射脉冲波的，雷达接收到回波时，会被认为是刚刚发射的脉冲波被气象目标散射所造成的，因此位于最大探测距离上的目标的回波信号必须在下一个脉冲波发射之前回到雷达天线。由此，我们可以得出雷达的最大探测距离 \(R_{\mathrm{max}}\) 公式：

\[R_{\mathrm{max}} = \frac{1}{2} \times \mathrm{PRT} \times c = \frac{1}{2} \times \frac{c}{\mathrm{PRF}} \]

式中 \(c\) 为光速。例如，711 雷达的脉冲重复频率为 400Hz，它的最大探测距离为 300km；713 雷达的脉冲重复频率为 200Hz，它的最大探测距离为 600km。

由上式可知，脉冲重复频率越高的雷达，其最大探测距离越小。不过，脉冲重复频率高的雷达，在一定时间内雷达接收到的回波信号较多，有利于在短时间内得到比较准确的平均回波强度，同时荧光屏上显示的回波也比较明亮清晰。

4.1.3 脉冲宽度和脉冲长度

探测脉冲持续震荡的时间称为脉冲宽度 \(\tau\)。探测脉冲具有一定的持续时间，从而空间上有一定的长度，称为脉冲长度 \(h\)。它们的关系如下：

\[h = \tau c \]

注意：脉冲宽度指的是一个脉冲持续多长，而脉冲重复频率指的是一秒钟内脉冲有多少个。

为精确测定降水区的大小和内部结构，天气雷达通常采用较窄的脉冲宽度。脉冲宽度一般为 1us 或 2us。有的天气雷达为了适应探测不同距离目标的需要，有几种脉冲宽度。在探测近目标时采用较窄的脉冲宽度；在探测远目标如晴空回波时，为增大回波信号的强度，采用较宽的脉冲宽度（4us）。

4.1.4 脉冲发射功率

脉冲发射功率 \(P_t\) 是指发射机发射脉冲波期间产生的高频功率，脉冲功率也叫峰值功率。脉冲功率越大，雷达接收到来自云雨的回波就越强，且雷达可以探测距离更远的目标。平均功率 \(\overline{P}_t\) 是指脉冲发射功率在其重复周期内的平均值，其计算公式为：

\[\overline{P}_t = \frac{P_t \times \tau}{T} \]

CINRAD/SA 的脉冲发射功率在 650～800kW 之间，脉冲峰值功率大于 750kW。

4.2 与天线相关的参数

4.2.1 天线方向图和波束宽度

为了表示雷达天线向外辐射电波能量的方向性情况，绘制出天线方向图。天线方向图应该是一个以天线位置为原点的立体图，为了便于理解，一般采用原点的纵切剖面（垂直面）和横切剖面（水平面）表示。下图即为纵切剖面示意图：

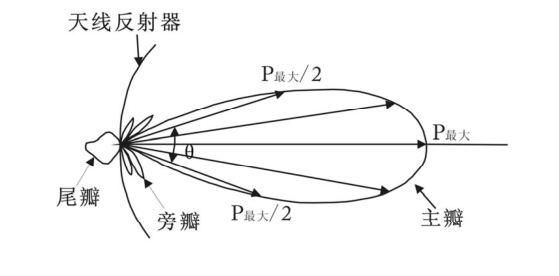
可以看到，图中水平方向的辐射最强，说明天线是被指定沿着该方向传播的，这就是定向辐射。所谓定向辐射是相对的，实际上定向天线只是在某一方向辐射最强，在其它方向辐射能量相对较少。图中，最大辐射能量的发射方向称为主瓣，侧面称为旁瓣或侧瓣，相反方向的称为尾瓣。当旁瓣较多时，从最接近主瓣的开始依次称为第一旁瓣、第二旁瓣。正因为发射的电磁波能量除了主瓣外还有旁瓣，所以在某些情况下会产生旁瓣回波，它是杂波的一种，后面文章将会介绍。

在天线方向图上，主瓣的两个半功率点（\(P_{\mathrm{max}} / 2\)）方向的夹角，称为波束宽度，也就是天线主瓣的宽度，它是天线的一个重要技术参数。在垂直面上的波数宽度用 \(\theta\) 表示，水平面上的波束宽度用 \(\phi\) 表示。波束宽度决定雷达径向探测精度，主瓣瓣宽越窄，角度分辨率越高，方向性越好，探测精度越高。

CINRAD/SA 的天线直径为 9m，波束宽度为 0.99°。

4.2.2 天线增益

天线增益是定向天线最大辐射方向上的功率密度 \(S_{\mathrm{max}}\) 和天线各向均匀辐射能量时同一距离上功率密度 \(S_{\mathrm{avg}}\) 的比值。天线增益数值越大，表示天线定向辐射的能力越强。天线增益用 \(G\) 表示，其定义式如下：

\[G = \frac{S_{\mathrm{max}}}{S_{\mathrm{avg}}} \]

除此之外，天线增益还与波束宽度存在关系：

\[G = \frac{\pi^2}{\theta \phi} \]

天线增益通常很大，一般用分贝数来表示。天线的尺寸越大，波长越短，天线增益就越高。较大的天线增益对于提高雷达探测能力和精度都是很有利的。所以，天气雷达通常具有较大的天线。CINRAD/SA 的天线增益大于 44dB。

4.3 雷达气象方程

在学习了前面的内容后，我们知道，雷达回波的强度取决于雷达参数，云雨物理特性，以及其与雷达之间的距离。那如何集中反映雷达回波强弱与雷达参数、云雨物理特性和雷达距离的关系呢？这就是雷达气象方程要做的事情。

4.3.1 单个目标的雷达气象方程

在此处我们就省略推导，直接给出对于单个目标的雷达气象方程：

\[P_r = \frac{P_t G^2 \lambda ^2}{(4 \pi)^3 r^4} \]

式中，\(P_r\) 为雷达所接收的功率，\(P_t\) 为发射功率，\(\lambda\) 为电磁波的波长，\(r\) 为气象目标和雷达的距离。可以看出，单个目标的雷达回波功率与距离成反比，随着距离的增大，回波功率迅速减小。

上述是天线辐射强度均匀分布时的雷达气象方程，事实上，我们做了个假设：天线辐射强度在两个半功率点间是均匀分布的。但实际上分布一般是不均匀的，为此需引入天线方向图函数，这里直接给出推导结果：

\[P_r = \frac{P_t G^2 \sigma \lambda ^2}{(4 \pi)^3 r^4} |f(\theta, \phi)|^4 \]

式中，\(\sigma\) 为粒子的后向散射截面，\(f(\theta, \phi)\) 即为天线方向图函数，可以与之前讲过的散射函数作类比，天线方向图函数也是反映天线辐射强度在波束宽度内的分布情况。

4.3.2 粒子群的雷达气象方程

现实情况是，雷达探测云和雨的时候，并不是单个气象目标，而是一群气象目标（即粒子群）。这些粒子相对雷达的位置作不规则运动，回波存在起伏现象。因此，需要考虑粒子群的雷达气象方程。

如果只考虑来自波束宽度 \(\theta\) 和 \(\phi\) 范围内粒子的散射，并假定在此范围内雷达的辐射强度是均匀的，则可得到雷达气象方程为：

\[\overline{P}_r = \frac{P_t G^2 \lambda ^2 h \theta \phi}{512 \pi^2 r^2} \sum_{i=1}^{N} \sigma_i \]

注意，此式求得的是来自降水区的回波功率的时间平均值 \(\overline{P}_r\)。式中 \(h\) 为脉冲长度，于 4.1.3 节介绍过。

但是天线辐射功率密度一般是不均匀的，需乘以一个订正因子 \(\frac{1}{2 \ln 2} = 0.72\)，于是上式又变为：

\[\overline{P}_r = \frac{P_t G^2 \lambda ^2 h \theta \phi}{1024(\ln 2) \pi^2 r^2} \sum_{i=1}^{N} \sigma_i \]

回忆在介绍散射那篇文章给出的雷达反射率 \(\eta\) 的定义：单位体积内全部降水粒子的雷达截面之和，因此上式可写为：

\[\overline{P}_r = \frac{P_t G^2 \lambda ^2 h \theta \phi}{1024(\ln 2) \pi^2 r^2} \eta \]

该方程对瑞利散射和米散射均适用。