一个贝塞尔曲线编辑工具(2d)

曲线在unity下如何绘制？

类似绘制圆，是用一段一段的线段拼接来模拟的，这边也是类似，可以用一段一段的线段来模拟曲线。

 

既然要模拟，那我们也得知道贝塞尔曲线的公式才行。

一般用的比较多的就是3次贝塞尔曲线，该曲线由起点p1，p1的控制点c1，终点p2，p2的控制点c2组成。

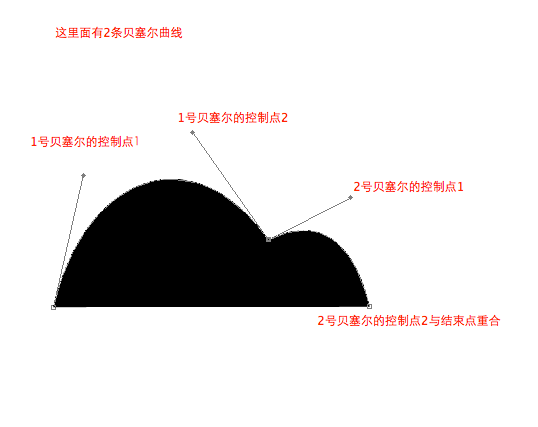
公式为：p = p1*(1-t)³ + 3*c1*t*(1-t)² + 3*c2*t²*(1-t) + p2*t³，t的范围[0, 1]

 

下面是unity下的一个贝塞尔编辑工具

 

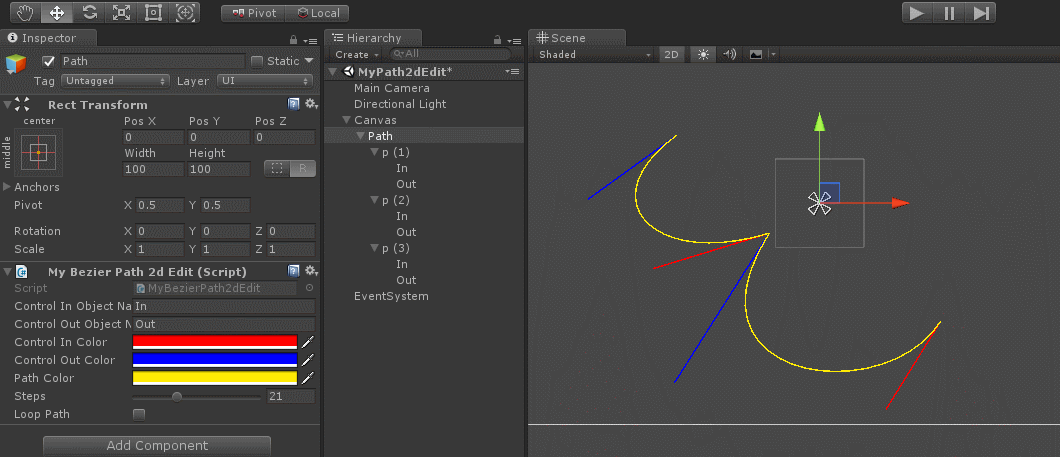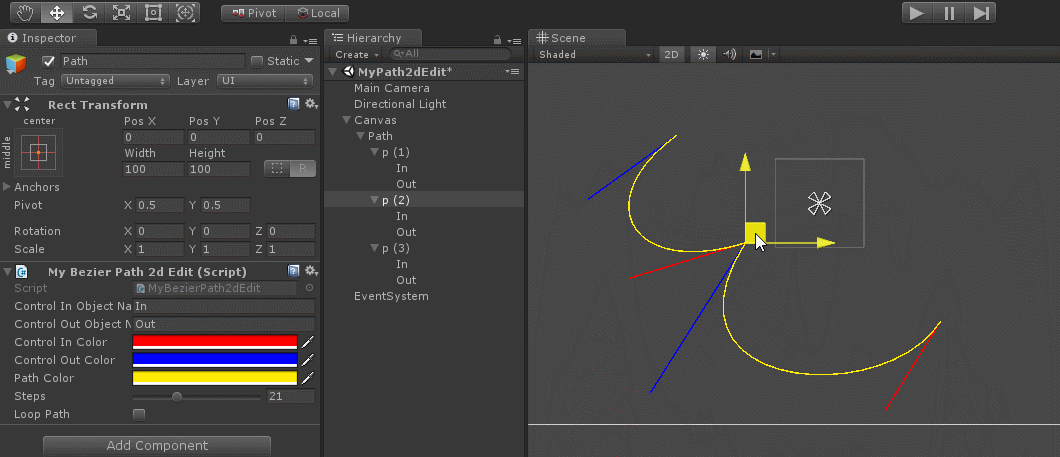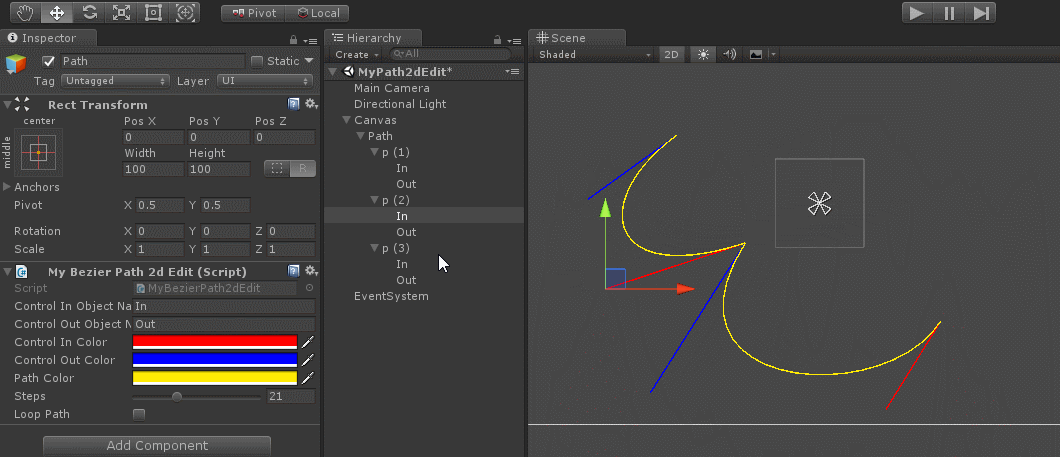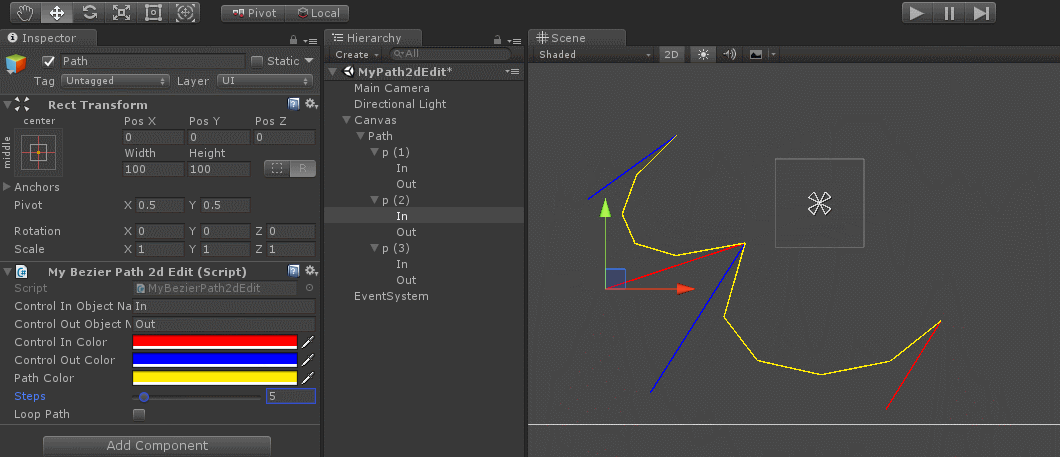
public class MyBezierPath2dEdit : MonoBehaviour
{public string m_ControlInObjectName = "In"; //作为曲线结束时, c2控制点public string m_ControlOutObjectName = "Out"; //作为曲线启示点时, c1控制点public Color m_ControlInColor = Color.red; //c2控制点连线颜色public Color m_ControlOutColor = Color.blue; //c1点连线颜色public Color m_PathColor = Color.yellow; //路径绘制颜色
[Range(1, 60)]public int m_Steps = 30; //曲线用多少个直线来模拟public bool m_LoopPath = false; //曲线是否首尾连接private void OnDrawGizmos(){var mainPoints = new List<Vector2>();var In = new List<Vector2>();var Out = new List<Vector2>();bool isAddRectTransform = null != GetComponent<RectTransform>();foreach (Transform child in transform){mainPoints.Add(child.transform.position);foreach (Transform child2 in child.transform){if (child2.name == m_ControlInObjectName)In.Add(child2.transform.position);if (child2.name == m_ControlOutObjectName)Out.Add(child2.transform.position);}//如果没有定义的点，则补充上去if (In.Count < mainPoints.Count){GameObject go = new GameObject(m_ControlInObjectName);if (isAddRectTransform)go.AddComponent<RectTransform>();go.transform.SetParent(child.transform, false);In.Add(go.transform.position);}if (Out.Count < mainPoints.Count){GameObject go = new GameObject(m_ControlOutObjectName);if (isAddRectTransform)go.AddComponent<RectTransform>();go.transform.SetParent(child.transform, false);Out.Add(go.transform.position);}}//曲线控制线for (int i = 0; i < mainPoints.Count; i++){Gizmos.color = m_ControlInColor;Gizmos.DrawLine(mainPoints[i], In[i]);Gizmos.color = m_ControlOutColor;Gizmos.DrawLine(mainPoints[i], Out[i]);}Gizmos.color = m_PathColor;if (In.Count >= mainPoints.Count && Out.Count >= mainPoints.Count){int mainPtCnt = mainPoints.Count;if (!m_LoopPath) mainPtCnt--;for (int i = 0; i < mainPtCnt; i++){int i2 = (i + 1) % mainPoints.Count;Vector3 P2 = new Vector3(0, 0, 0);float step = 1.0f / m_Steps;if (step > 0.01f){for (float t = 0; t < 1 + step; t += step){Vector3 P1 = P2;P2 = CalcBezierPathPoint(mainPoints[i], Out[i], In[i2], mainPoints[i2], t);if (t > 0){Gizmos.DrawLine(P1, P2);}}}}}}private Vector3 CalcBezierPathPoint(Vector3 P0, Vector3 C0, Vector3 C1, Vector3 P1, float t){float temp = 1 - t;Vector2 result = temp * temp * temp * P0 + 3 * temp * temp * t * C0 + 3 * temp * t * t * C1 + t * t * t * P1;return result;}}