【逆运动学2】damped least squares method阻尼最小二乘法

逆运动学

 逆运动学，就是从操作空间的end effector position and orientation，求关节空间的joint position的问题。在之前的文章，我们简单提到求逆运动学解的解析解法和优化解法，详细讲解了用逆瞬时（或说微分）运动学即雅可比矩阵法迭代求解逆运动学的方法。这篇文章我们继续讲雅可比矩阵求逆法存在的问题、用以对付Singularity问题的阻尼最小平方法，并详细地讲讲雅可比矩阵转置法。

雅可比矩阵求逆法复习

 雅可比矩阵求逆法，就是利用下面式子所示的关节速度与end effector速度的关系，迭代求解逆运动学问题的方法。

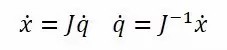
 我们可以用一个控制框图来表示这个求解过程：

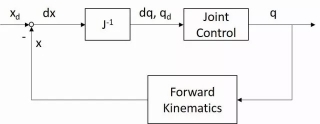
 这个方法把复杂的逆运动学运算（解析法和优化法）转化为求解线性方程的运算，具有很好的通用性；然而这个方法也存在一些问题。

雅可比矩阵求逆法存在的问题

 从原理上讲，使用这个方法最明显的一点要求是——dx不能过大。因为Jacobian是随着关节位置变化不断在变化的，一旦关节位置变化很大，算出来的Jacobian Inverse就不再准确了。这个问题通常我们可以用轨迹线性插值（linear interpolation）或限制dx的大小（clamping）来避免。

 这个方法的第二个难点是雅可比矩阵求逆运算。矩阵求逆是一个非常消耗计算资源的运算（在写程序时能避免就绝对不要求逆！）。当然，我们总是可以使用各种各样的解线性方程的方法来避开求逆运算，比如LU分解、Chelosky分解、QR分解、SVD（Singular Value Decomposition）等等——这个以后也可以考虑用来填几篇干货了……

 这个方法最大的问题还是在于它无法很好地对付机器人Singularity或接近Singularity的情况。从线性方程的角度看，当机器人接近Singularity时，雅可比矩阵也越来越“病态”（ill-conditioned），很小的dx可能求得很大的dq，方程对数值误差也更加敏感；而当机器人处于Singularity时，线性方程可能无解、也可能有无数多个解。

DLS（Damped Least Square，阻尼最小平方法）

 为了避免利用雅可比矩阵求逆法控制机械臂时由于接近Singularity而产生非常大的关节速度，一个自然的想法就是在求解过程中限制关节速度——既要尽可能地满足方程条件、也要尽可能地让关节速度不要太大。

 对于前者，我们可以用最小平方法求解方程，这时问题可以这样表述：

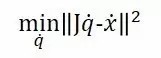
 即求一个dq，使Jdq - dx的norm（向量范数，可以理解为衡量向量距离的一种指标）的平方最小；理想情况下等式左右相等，这个norm则为0。

 对于后者，即是希望||dq||尽可能小（但显然通常情况下不能为0），此时我们可以把上面的式子后面再加一个“阻尼”项，变成这样：

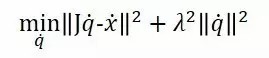
 即求一个dq，使Jdq-dx的norm的平方，加上乘以一个系数的dq的norm的平方，它们的和最小。这个时候，λ的大小决定了你更“看重”哪一个条件：如果λ很大，那可能你求得一个很小的关节运动速度，但这个速度却不能准确地让end effector按照你所希望的轨迹走；如果λ很小，小到接近于0，那这个方法跟之前的最基础的Jacobian Inverse算法也没有什么两样了。在实际使用，λ的大小往往需要仔细选择。

 求解上面那个式子的最小值，还是用我们伟大的导数求极值法：

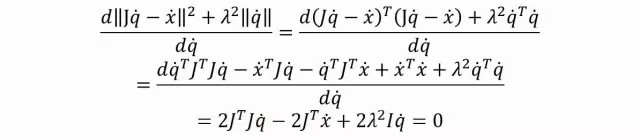
（这么详细的求导过程就算看不懂也要记住啊！极其重要，随处可见）

 于是我们得到一个等效方程：

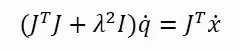
 能够证明左边的系数矩阵是可逆的，于是我们就有了解：

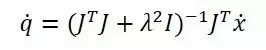
 能看出显然以下式子也是相等的：

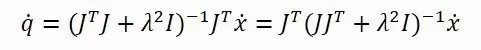
 知道这个有什么用呢？因为左边需要求逆的矩阵大小为n×n，n为关节数量，要多大有多大；右边需要求逆的矩阵大小为m×m，m为操作空间的自由度大小，最大肯定不超过六。这个小小的转换，就限制了需要求逆运算的矩阵大小，提高了总体的运算速度。

雅可比矩阵转置法

 上次我们简单地讲到说，我们可以用雅可比矩阵的转置代替求逆运算来求逆运动学问题：

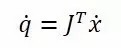
 今天我们详细地讲下这个看起来很随便的方法是怎么推导出来的。

 首先明确求解逆运动学问题，我们的终极目标是控制机械臂的各个关节，让机械臂的end effector运动到我们想要它到达的位置及朝向。我们把这个“理想位置”计为xd，我们的目标就是要让当前end effector位置xc与xd的“距离”最短。于是我们又有了一个数学问题：

 注意上面式子中我们要求的是q，而不是dq。乘上1/2是为了求导后不要有讨厌的系数2。

 用正运动学的表达式可以把xc用f(q)表示：

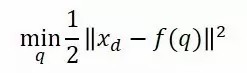
（也许你已经发现了这个就是把逆运动学转化为优化问题的优化法）。

 由于正运动学的表达式f(q)通常比较复杂，导数极值法在这里不太好用。所以我们祭出求极值的另一个伟大工具：梯度下降法（Gradient Descent）。

 梯度下降法说，每一步我都要沿着下降最快的那个方向走，而这个方向可以由梯度的反方向求得，所以我们有：

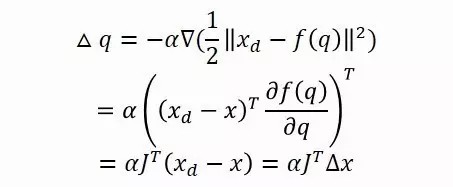
 这个推导证明了如果我们用梯度下降大法，每一步都用J的转置乘dx求出dq，那么机械臂迭代几步以后end effector将无限趋近指定的xd。它的迭代框图其实与雅可比矩阵求逆法是一样的，只是J-1换成了JT。

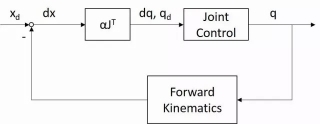
 上面的α也是梯度下降法的一个系数，叫“步长”（step size）或“学习速率”（learning rate)。这个值太小，则迭代速度可能太慢；这个值太大，则可能“走过头”或要多绕一些弯路，最终还是使迭代速度变慢（甚至无法收敛到最小值）。

 采用雅可比矩阵转置而不是求逆的方法，最大的好处当然是避免了求逆运算；不过与求逆相比，它的迭代收敛速率反而慢些。另外，用这个方法控制的机械臂，离end effector较远的关节常常需要输出更大的扭矩。

 关于逆运动学的这两篇文章，可以说讲了机器人学家们与逆运动学问题斗智斗勇的过程；我们简单提到解析法和优化法，讲了雅可比矩阵求逆迭代法、阻尼最小平方法、以及实质上也是优化和迭代方法的雅可比矩阵转置法。然而这只是逆运动学问题求解方法中比较有代表性的一小部分。

摘抄自WX公众号：Robotics