【学习笔记】并查集应用

【学习笔记】并查集应用

以 NOI 2001 食物链 为例の两种并查集用法。

题目大意：

规定每只动物有且仅有三种可能的种类 \(A、B、C\)，\(A\) 会吃 \(B\)，\(B\) 会吃 \(C\)，\(C\) 会吃 \(A\)。

给定 \(N\) 只动物，\(K\) 个语句。每个语句有如下两种可能的表达：

1. 1 X Y 表示动物 \(X\) 与动物 \(Y\) 是同类。

2. 2 X Y 表示动物 \(X\) 吃 \(Y\)。

每个语句可能是真话也可能是假话，每个语句是假话有三种可能：

1. \(X\) 或 \(Y\) 比 \(N\) 大。

2. 表达为 \(X\) 吃 \(X\)。

3. 当前的话与前面的某些真的话冲突。

请求出 \(K\) 个语句里假话的总数。

种类并查集（扩展域并查集）

先推一个讲解。

并查集能维护连通性、传递性，通俗地说，亲戚的亲戚是亲戚。

然而当我们需要维护一些对立关系，比如敌人的敌人是朋友时，正常的并查集就很难满足我们的需求。

这时，种类并查集就诞生了。

在同个种类的并查集中合并，表达他们是朋友这个含义。

在不同种类的并查集中合并，表达他们是敌人这个含义。

---

此题关系有三类（\(A、B、C\)），所以我们考虑建立 3 倍大小的并查集。其中 \(1 \sim n\) 表示种类 \(A\)，\(n+1 \sim 2n\) 表示种类 \(B\)，\(2n+1 \sim 3n\) 表示种类 \(C\)。

如果两只动物 \(x\) 和 \(y\) 是同类，那么就将 \(A_x\) 与 \(A_y\)，\(B_x\) 与 \(B_y\)，\(C_x\) 与 \(C_y\) 各并入一个集合内。

如果两只动物 \(x\) 吃 \(y\)，那么就将 \(A_x\) 与 \(B_y\)，\(B_x\) 与 \(C_y\)，\(C_x\) 与 \(A_y\) 各并入一个集合内。

此时如果要表示动物 \(x\) 吃动物 \(y\)，就说明 \(A_x\) 与 \(B_y\) 在同一集合中，根据对称性，其它的也一样，所以判断时只需要判一组。

• \(x\) 与 \(y\) 同类与 \(x\) 吃 \(y\) 或 \(y\) 吃 \(x\) 矛盾。
• \(x\) 吃 \(y\) 与 \(x\) 与 \(y\) 同类或 \(y\) 吃 \(x\) 矛盾。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 5e4+5;int fa[N*3];int find(int x){if(fa[x] == x) return x;return fa[x] = find(fa[x]);
}int main(){ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);int n, k, ans = 0; cin>>n>>k;for(int i=1; i<=n*3; i++)fa[i] = i;while(k--){int op, x, y; cin>>op>>x>>y;if(x==y&&op==2 || x>n || y>n){ans++;continue;}if(op==1){if(find(x)==find(y+n) || find(y)==find(x+n)){ans++;continue;}fa[find(x)] = fa[find(y)];fa[find(x+n)] = fa[find(y+n)];fa[find(x+n+n)] = fa[find(y+n+n)];} else if(op==2){if(find(x)==find(y) || find(y)==find(x+n)){ans++;continue;}fa[find(x)] = fa[find(y+n)];fa[find(x+n)] = fa[find(y+n+n)];fa[find(x+n+n)] = fa[find(y)];}}cout<<ans;return 0;
}

带权并查集

每个点与其集合的根都有权重，以此来表达关系。

以此题为例，0 代表 \(x\) 与 \(fa_x\) 同类，1 代表 \(x\) 吃 \(fa_x\)，2 代表 \(x\) 被 \(fa_x\) 吃。

重点在于如何更新权值和判断关系。权值更新肯定伴随并查集的更新。在下面的图中就如向量一般计算。

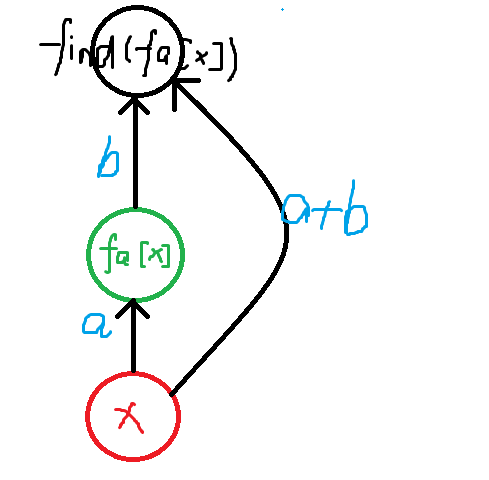
查找（路径压缩）：

知道 \(x\) 与其根 \(fa[x]\) 的关系，\(fa[x]\) 与其根 \(fa[fa[x]]\) 的关系，可以推出 \(x\) 与 \(fa[fa[x]]\) 的关系。

注意这里要先更新 \(fa[x]\) 的权值（先 find(fa[x])），在更新 \(x\) 的权值（得先存下 \(fa[x]\)，不然 \(fa[x]\) 会变）。

\[rel[x \rightarrow rt] = rel[x \rightarrow fa]+rel[fa \rightarrow rt] \]

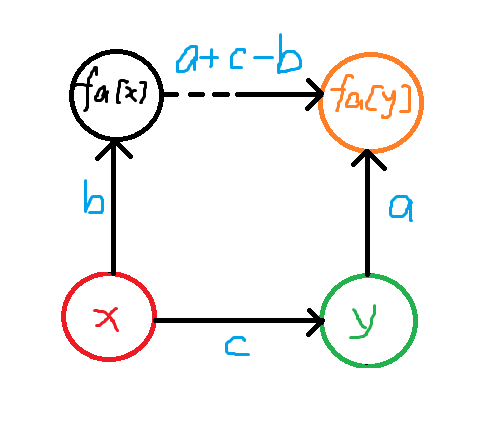
合并：

知道 \(x\) 与 \(fa[x]\) 的关系，\(y\) 与 \(fa[y]\) 的关系，以及 \(x\) 与 \(y\) 之间的关系，就可以知道 \(fa[x]\) 和 \(fa[y]\) 的关系。

注意是 \(fa[x]\) 并到 \(fa[y]\) 上还是 \(fa[y]\) 并到 \(fa[x]\) 上。以下是 \(fa[x]\) 并到 \(fa[y]\) 上。

\[rel[fa[x]] = rel[y]-rel[x]+rel[x \rightarrow y] \]

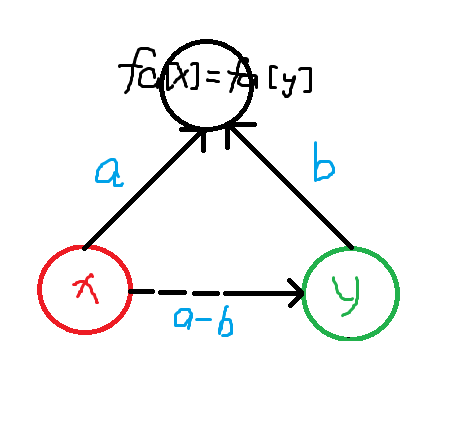
判断关系（是否矛盾）：

知道 \(x、y\) 与根的关系，就能推出 \(x\) 与 \(y\) 的关系。（此时 \(x\) 与 \(y\) 已经在同一个集合内）

\[rel[x \rightarrow y] = rel[x]-rel[y] \]

以上操作取模时注意减法，显然此题模数为 \(3\)。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 50005;int fa[N], rel[N];
// relation 存与根的关系
// 0--同类，1--能吃，2--被吃
const int p = 3;
int n, k, ans;void init(){for(int i=1; i<=n; i++){fa[i] = i;rel[i] = 0;// 初始化跟自己的关系是同类}
}int find(int x){if(fa[x] == x) return x;// 知道 x 与 fa[x] 的关系，fa[x] 与根的关系，可以推出 x 与根的关系// rel[x->rt] = rel[x->fa]+rel[fa->rt]int f = fa[x];fa[x] = find(fa[x]);rel[x] = (rel[x]+rel[f])%p;// 必须得分开写，因为原来的 fa[x] 与根的关系会在 find(fa[x]) 的时候更新return fa[x];
}void merge(int u, int v, int r){// U与rtU的关系，V与rtV的关系，以及UV之间的关系，就可以知道rtU和rtV的关系。// rtU 并到 rtV 上// rel[ru] = rel[v]-rel[u]+rel[u->v]int ru = find(u), rv = find(v);if(ru != rv){fa[ru] = rv;rel[ru] = (rel[v]-rel[u]+r+p)%p;}
}bool check(int x, int y, int r){if(x>n || y>n) return false; // 不能比 n 大if(x==y && r==1) return false; // 不能吃自己if(find(x)==find(y)){// 知道x、y与根的关系，就能推出 x 与 y 的关系// rel[x->y] = rel[x]-rel[y]return r == (rel[x]-rel[y]+p)%p;}return true;// 还没明确的关系就是可行的
}int main(){ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin>>n>>k;init();while(k--){int op, x, y; cin>>op>>x>>y;if(check(x, y, op-1)){merge(x, y, op-1);} else{ans++;}}cout<<ans;return 0;
}