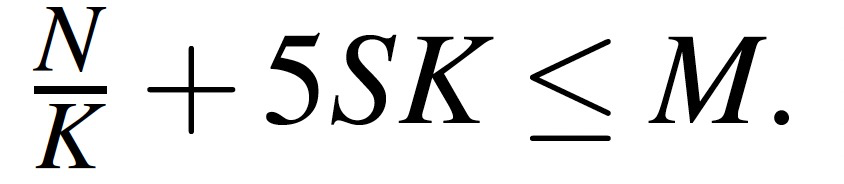The Normal Distributions Transform: A New Approach to Laser Scan Matching
正态分布变换:激光扫描匹配的新方法
摘要:匹配 2D 范围扫描是许多定位和建图算法的基本组成部分。大多数扫描匹配算法需要找到所使用的特征(即点或线)之间的对应关系。我们提出了范围扫描的替代表示法,即正态分布变换。与占用网格类似,我们将 2D 平面细分为单元。对于每个单元格,我们分配一个正态分布,该分布对测量点的概率进行局部建模。变换的结果是分段连续且可微的概率密度,可用于使用牛顿算法匹配另一次扫描。因此,不必建立明确的对应关系。我们详细介绍了该算法,并展示了其在相对位置跟踪以及同步定位和地图构建 (SLAM) 中的应用。真实数据的初步结果表明,即使不使用里程计数据,该算法也能够可靠且实时地绘制未修改的室内环境(参见视频)。
一、引言
毫无疑问,同步定位与建图(SLAM)是移动机器人系统的基本能力。激光测距扫描仪是获得所需输入的流行传感器,主要是因为它们在国外的情况下具有高可靠性和低噪声。许多 SLAM 算法基于匹配两个范围扫描或将范围扫描与地图匹配的能力。在这里,我们提出了一种扫描匹配低级任务的新方法,并展示了我们如何使用它来构建地图。
本文的主要目的是介绍正态分布变换(以下称为NDT)及其在一次扫描与另一次扫描或一次扫描与多个其他扫描的匹配中的应用。 NDT 将从单次扫描重建的离散 2D 点集转换为在 2D 平面上定义的逐个连续且可微的概率密度。该概率密度由一组可以轻松计算的正态分布组成。然后将第二次扫描与 NDT 匹配定义为最大化第二次扫描在该密度上的对齐点得分的总和。
我们还提出了一种针对 SLAM 问题的简单算法,该算法很好地融入了我们的匹配方案。然而,所提出的匹配方案并不依赖于该算法。因此,我们仅回顾第二节相关工作中有关两次扫描匹配的方法,而不回顾像 Thrun [15] 或 Gutmann [6] 的方法那样构建整个地图的方法。然而,这种方法的一个组成部分是感知模型,即给定 amap 和 apose 估计的单次扫描的可能性。由于我们的方法可以精确测量此类模型,因此我们相信,我们的扫描匹配器也可以集成到更复杂的 SLAM 算法中。
本文的其余部分组织如下:第三节介绍了 NDT,第四节概述了扫描匹配方法,并定义了将 ascan 与 aNDT 进行比较的度量,该度量在第五节中使用牛顿算法进行了优化。扫描匹配器应用于第六节中的位置跟踪和第七节中的简单 SLAM 方法。我们最终展示了一些真实数据的结果,并对未来的工作进行了展望。
II.P 先前工作
匹配两个范围扫描的目标是找到进行扫描的两个位置之间的相对位置。最成功算法的基础是在两次扫描的基元之间建立对应关系。由此,可以导出误差测量并将其最小化。 Cox 使用点作为基元并将它们与先验模型中给出的线相匹配 [3]。在阿莫斯项目 [7] 中,这些线条是从扫描中提取的。 Gutmann 将从 ascan 中提取的线条与模型中的线条进行匹配 [8]。 Lu 和 Milios [9] 提出了最通用的方法,即点对点匹配。这本质上是应用于激光扫描匹配的 ICP(迭代最近点)算法 ([1]、[2]、[18]) 的变体。我们与 Lu 和 Milios 分享我们的映射策略。如[10]中所示,我们不构建显式地图,而是使用选定扫描的集合及其恢复的姿势作为隐式地图。
在所有这些方法中,必须建立明确的对应关系。我们的方法在这一点上有所不同,因为我们永远不需要在基元之间建立对应关系。还有其他方法可以避免解决对应问题。在[12]中,Mojae v 将局部极地占用网格的相关性与概率测距模型相结合,用于姿态确定(使用激光扫描仪和声纳)。 Weiss 和 Puttkammer [17] 使用角度直方图来恢复两个姿势之间的旋转。然后使用找到最常见方向后计算的 x 和 y 直方图来恢复平移。这种方法可以通过使用第二个主要方向来扩展[7]。
我们的工作也受到计算机视觉技术的启发。如果用图像强度代替单词概率密度,我们的方法与特征跟踪[13]或全景图合成[14]具有相似的结构。这些技术使用每个相关位置的图像梯度来估计参数。这里,使用正态分布的导数。与图像梯度相反,这些可以通过分析计算。
III.正态分布变换
本节描述单次激光扫描的正态分布变换(NDT)。这意味着本文的核心贡献。使用 NDT 进行位置跟踪和 SLAM(在以下各节中描述)相对简单。 NDT 通过局部正态分布的集合对一次激光扫描的所有重建 2D 点的分布进行建模。首先,机器人周围的二维空间被规则地细分为大小恒定的单元。然后,对于每个包含至少三个点的单元格,执行以下操作:

现在,在该单元中包含的 2D 点 x 处测量样本的概率由正态分布 N (q; ∑) 建模:

与占用网格类似,NDT 建立了平面的常规细分。但是,占用网格表示单元被占用的概率,而 NDT 则表示测量单元内每个位置的样本的概率。我们使用 100 厘米 x 100 厘米的单元尺寸。
这个表示有什么用呢?我们现在以概率密度的形式对二维平面进行了分段连续且可微的描述。在展示示例之前,我们必须注意两个实现细节。为了最大限度地减少离散化的影响,我们决定使用四个重叠的网格。也就是说,首先放置一个边长为 l 的单个单元格,然后放置第二个网格,水平移动 L/2 ,第三个,垂直移动 L/2 ,最后移动第四个,水平和垂直移动 L/2 。没有一个 2D 点落入四个单元格中。本文的其余部分不会明确考虑这一点,我们将描述我们的算法,就好像每个点只有一个单元格一样。所以计算一个点的概率密度时,默认是对所有四个单元格的密度进行评估,然后将结果相加。
第二个问题是,对于无噪声的测量世界线,协方差矩阵将变得奇异并且无法反转。在实践中,协方差矩阵有时会接近奇异值。为了防止这种影响,我们检查的较小特征值是否至少是较大特征值的 0:001 倍。如果不是,则设置为此值。

图 1. NDT 示例:原始激光扫描和生成的概率密度。
图 1 显示了激光扫描示例和所得 NDT 的可视化。可视化是通过评估每个点的概率密度创建的,明亮区域表示高概率密度。下一节将展示如何使用此转换来对齐双激光扫描。
IV.扫描对准
两个机器人坐标系之间的空间映射 T 由下式给出

其中 ![]() 描述两个帧之间的平移和旋转。扫描对准的目标是使用在两个位置进行的激光扫描来恢复这些参数。考虑到两次扫描(第一次和第二次),所提出的方法的概要如下:
描述两个帧之间的平移和旋转。扫描对准的目标是使用在两个位置进行的激光扫描来恢复这些参数。考虑到两次扫描(第一次和第二次),所提出的方法的概要如下:
1) 建立第一次扫描的NDT。
2) 初始化参数的估计(通过零或使用里程计数据)。
3)对于第二次扫描的每个样本:根据参数将重建的二维点映射到第一次扫描的坐标系中。
4) 确定每个映射点对应的正态分布。
5) 参数的得分是通过评估每个映射点的分布并对结果求和来确定的。
6) 通过尝试优化分数来计算新的参数估计。这是通过执行牛顿算法的一个步骤来完成的。
7) 转到3,直到满足收敛标准。
前四个步骤很简单:上一节描述了构建 NDT。如上所述,里程计数据可用于初始化估计。使用 T 完成第二次扫描的映射,并在 NDT 网格中进行简单查找即可找到相应的正态分布
现在使用以下符号详细描述其余部分:

如果评估具有参数 ∑i 和 qi 的所有点 xi 的正态分布之和最大,则根据 p 的映射可以被认为是最优的。我们将此总和称为 p 的分数。定义为:

该分数将在下一节中进行优化。
V.使用牛顿算法进行优化
由于优化问题通常被描述为最小化问题,因此我们将采用我们的符号来表示此约定。因此,本节中要最小化的函数是分数。牛顿算法迭代地找到参数 p =( pi)t ,从而最小化函数 f 。每次迭代都求解以下方程:

其中 g 是 f 与条目的转置梯度

H 是 f 的 Hessian 矩阵,有条目

该线性系统的解是一个增量 p,它被添加到当前估计中:

如果 H 是正定的,f (p) 最初将沿 p 的方向减小。如果不是这种情况,则将 H 替换为 H0 = H + I,选择这样的方式,使得 H0 安全地为正定。有关最小化算法本身的实际细节可以在 [4] 中找到。
该算法现在应用于函数得分。通过收集方程3的所有被加数的偏导数来构建梯度和Hessian矩阵。为了更简短的表示法并避免混淆参数编号i和激光扫描样本i的索引,省略了样本编号的索引i。另外,我们写

很容易验证,q 对 p 的偏导数等于 x0i 的偏导数。得分的一个被加数 s 由下式给出

对于这样的被加数,梯度的条目是(使用链式法则):

q 对 pi 的偏导数由 T 的雅可比矩阵 JT 给出(参见方程 2):

Hessian H 中的被加数条目由下式给出:

q 的二阶导数为(参见方程式 11):

从这些方程可以看出,构建梯度和 Hessian 矩阵的计算成本很低。每个点只需调用一次指数函数和少量乘法。三角函数仅取决于(角度的当前估计),因此每次迭代只能调用一次。接下来的两节将使用该算法进行位置跟踪和 SLAM。
VI.位置跟踪
本节描述如何应用扫描匹配算法来从给定时间 t = tstart 开始跟踪当前位置。下一节将这种方法扩展到 SLAM。此时全局参考坐标系由机器人局部坐标系定义。相应的激光扫描在下文中被称为关键帧。跟踪是针对该关键帧执行的。在时间 tk 时,算法执行以下步骤:
1) 让 为时间 tk 1 和 tk 之间运动的估计(例如来自里程计)。
2) 根据 绘制时间 tk 1 的位置估计。
3) 使用当前扫描、关键帧的NDT和新位置估计来执行优化算法。
4) 检查关键帧是否足够“接近”当前扫描。如果是的话,迭代。否则将最后一次成功匹配的扫描作为新的关键帧。
ascan 是否仍然足够接近的决定基于一个简单的经验标准,涉及关键帧和当前帧之间的平移距离和角距离以及所得分数。为了对位置跟踪有用,该算法必须实时执行:在 1.4 GHz 机器上构建 ascan 的 NDT 需要大约 10 毫秒。对于扫描之间的小移动,优化算法通常需要大约 1-5 次迭代(很少超过 10 次)。一次迭代需要2ms左右,所以实时性没有问题。
VII. SLAM 的应用
我们将地图定义为关键帧及其全局姿势的集合。本节描述当机器人到达未知区域时如何相对于该地图进行定位以及如何扩展和优化该地图。
A.关于多次扫描的定位
对于地图中的每个扫描i,角度i(或旋转矩阵Ri)和平移向量(tx;t y)it=Ti相关联。这些描述了全局坐标系中扫描 i 的位姿。当前机器人位姿由旋转矩阵 R 和平移向量 T 表示。从机器人坐标系到扫描 i 的坐标系的映射 T 0 由下式给出:

只需要进行一些小的改变即可使第五节的算法适应这种情况。扫描 i 的二维点的映射现在通过应用 T 0 来计算。此外,T 0 的雅可比行列式和二阶偏导数现在变得稍微复杂一些。映射的雅可比行列式现在由下式给出:

T 0 的二阶偏导数现在由下式给出:

优化算法的梯度和 Hessian 矩阵可以通过对所有重叠扫描求和来构建。但我们找到了一种替代方案,速度更快,并且产生同样好的结果:对于在机器人位置采集的每个扫描样本,确定扫描,其中评估概率密度的结果最大。仅此扫描用于此样本和当前迭代。这样,除了找到上述最大值之外,为优化算法构建梯度和 Hessian 矩阵所需的操作与重叠关键帧的数量无关。
B. 添加新的关键帧并优化地图
在每个时间步,地图由一组关键帧组成,其姿态位于全局坐标系中。如果当前扫描与地图的重叠太小,则地图将由上次成功匹配的扫描扩展。然后,每个重叠扫描都分别与新的关键帧进行匹配,从而产生两次扫描之间的相对姿势。维护一个图,其中保存成对匹配结果的信息。
在此图中,每个关键帧都由阳极表示。节点保存全局坐标系中关键帧姿态的估计。两个节点之间的边表示相应的扫描已成对匹配,并保持两个扫描之间的相对位置。
添加新的关键帧后,通过优化在所有关键帧的参数上定义的误差函数来细化地图。成对配准的结果用于为每个匹配对定义二次误差模型,如下所示: 两次扫描的全局参数也定义两次扫描之间的相对位置。令 p 为全局参数定义的相对位姿与成对匹配结果定义的相对位姿之间的差。然后我们对分数进行建模使用二次模型将这两次扫描作为 p 的函数

因此,score 是两两匹配收敛时的最终分数,H 是由此获得的 Hessian 矩阵。该模型是通过分数在 p = 0 到二次项之间的泰勒展开而导出的。请注意,线性项缺失,因为我们围绕极值点展开。现在,该分数在所有边缘上求和并进行优化。
如果关键帧的数量变大,则无法再在实时条件下执行这种最小化(自由参数的数量为 3N 3,其中 N 是关键帧的数量)。因此,我们仅对地图的子图进行优化。该子图是通过收集所有关键帧来构建的,从新关键帧的节点出发,遍历不超过三个边即可到达该子图。我们现在仅针对属于该子图中包含的关键帧的参数来优化上面的误差函数。当然,如果必须关闭循环,我们就必须对所有关键帧进行优化。
八、结果
我们现在展示的结果(以及第 6 节中的示例)是在不使用里程计的情况下执行的。这应该证明该方法的稳健性。当然,正如 Thrun 在[15]中已经指出的那样,只要世界上存在任何二维结构,这才有可能。
图2 中呈现的构建地图。 2是通过驾驶机器人离开实验室,沿着走廊,沿着走廊,然后返回实验室而获得的。

图 2:使用我们的扫描匹配器构建的地图。长度以厘米为单位。显示的是关键帧集和估计轨迹(参见视频)。更多视频可以在作者的主页上找到[11]。
因此,这种情况既需要地图的扩展,又需要相对于地图的定位。该机器人在 20 分钟的行程中收集了 28430 次激光扫描,行程约 83 米。使用 SICK 激光扫描仪进行扫描,覆盖范围为 180 度,角分辨率为 1 度。为了模拟更高的速度,仅使用每第五次扫描。模拟速度约为 35 cm=s,每秒扫描次数约为 23 次。地图是使用组合策略构建的。第 4 节的位置跟踪器应用于每次扫描,而我们通过推断结果来初始化参数最后一个时间步是线性的。每第十次扫描,应用第七节的程序。
图 2 显示了生成的地图。显示的是最终地图包含的 33 个关键帧。仔细观察还发现,我们的扫描匹配算法可以容忍环境中的微小变化,例如打开或关闭的门。在 1.4 GHz 机器上处理 ine 的所有帧需要 58 秒,即每秒扫描 97 次。通过将我们当前的实现从 Java 移植到更快的语言,也许可以获得更快的速度。
IX. 结论和未来工作
我们提出了范围扫描的一种新表示方法,即正态分布变换(NDT)。该变换可用于导出用于匹配另一扫描的分析表达式。我们还展示了如何将我们的扫描匹配器应用于位置跟踪问题和 SLAM 问题。我们的方法的主要优点是:
- 不必在点或特征之间建立明确的对应关系。由于这是大多数方法中最容易出错的部分,因此我们在没有对应关系的情况下更加稳健。
- 所有导数都可以通过分析计算。这既快速又正确。
问题当然是:一切都可以通过局部正态分布很好地建模吗?
到目前为止,我们的测试都是在室内环境中进行的,这从来都不是问题。计划在结构较少的环境(最好是室外)中进行进一步的测试。我们还打算系统地比较我们的方法与 Lu 和 Milios 的方法的收敛半径。
X.致谢
Peter Biber 得到了巴登符腾堡州的资助,对此深表谢意。我们还要感谢 Andreas Zell 教授和 Achim Lilienthal 教授让我们能够使用机器人和数据采集软件。我们还要感谢 Sven Fleck 进行了多次富有成效的讨论并为视频提供了帮助。