性质一:最小圆覆盖是唯一的
证:若存在两个最小圆,如下
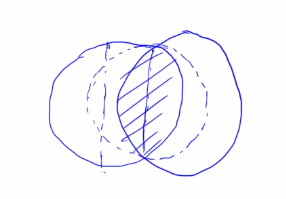
显然所有点只能存在于两个圆的交集中,于是以中间那条实心蓝线为直径做一个圆,这个圆显然更小而且能够覆盖所有点
性质二:若我们已经用最小覆盖圆覆盖了所有点,设这些点的点集为\(S\),现在我们新加入一个点\(p\),若\(p\)不在\(S\)的最小覆盖圆的内部,则\(p\)一定在{\(p\)}∪\(S\)的边上
证明:假设\(p\)在最小覆盖圆的外部,如下图:
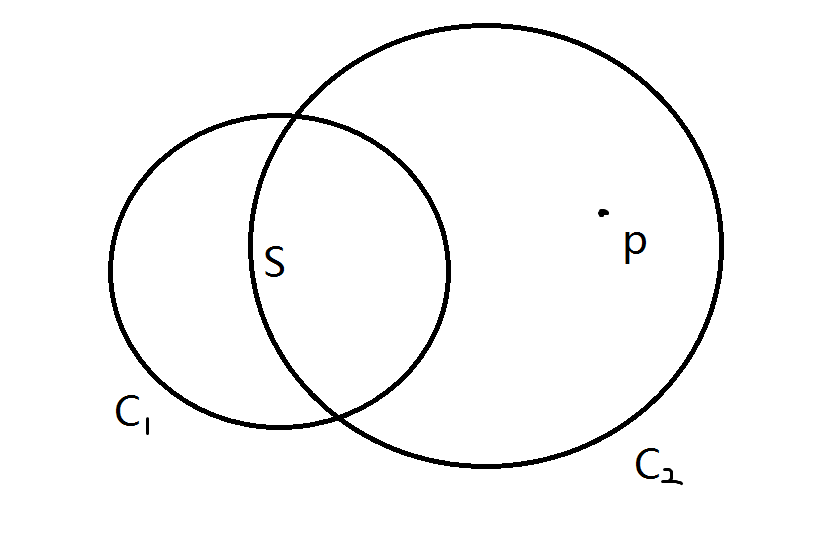
由于\(C_2\)覆盖了\(S\),所以\(r_{C_2}≥r_{C_1}\),由性质一,有\(r_{C_2}>r_{C_1}\),于是可以将\(C_2\)不断缩小,使其同时包含\(S\)和\(p\),这与\(C_2\)是最小圆覆盖矛盾
求最小覆盖圆思路:首先将点随机化保证复杂度。然后循环,假设循环到\(i\),我们已经求出了\(1\) ~ \(i-1\)的最小覆盖圆,如果\(i\)在这个最小覆盖圆内部,则圆不变,否则的话由性质二可以知道\(i\)一定在新的最小覆盖圆的边上。开一个内层循环,假设循环到\(j\),我们已经求出了\(1\) ~ \(j-1\)且\(i\)在圆边上的最小覆盖圆(我们要求的是\(1\) ~ \(j\)且\(i\)在圆边上的最小覆盖圆),如果\(j\)在这个最小覆盖圆内部,则圆不变(此时即使多了条件\(i\)在圆边上,我们仍然可以类似证明性质一),否则的话\(j\)一定在新的最小覆盖圆的边上(此时即使多了条件\(i\)在圆边上,我们仍然可以类似证明性质二)。再开一个内层循环,假设循环到\(k\),我们已经求出了\(1\) ~ \(k-1\)且\(i,j\)在圆边上的最小覆盖圆(我们要求的是\(1\) ~ \(k\)且\(i,j\)在圆边上的最小覆盖圆),如果\(k\)在这个最小覆盖圆内部,则圆不变(此时即使多了条件\(i,j\)在圆边上,我们仍然可以类似证明性质一),否则的话\(k\)一定在新的最小覆盖圆的边上(此时即使多了条件\(i,j\)在圆边上,我们仍然可以类似证明性质二),而此时我们已经确定了三个点在圆边上,于是可以唯一确定圆,从而求出了\(1\) ~ \(j\)且\(i\)在圆边上的最小覆盖圆,进而可以求出\(1\) ~ \(i\)的最小覆盖圆
时空复杂度都是\(O(n)\)(具体证明见视频39:30)
如果要求最小覆盖球,则是“四点确定一个球”,其余类似