原题链接在这里:https://leetcode.com/problems/number-of-ways-to-build-house-of-cards/description/
题目:
You are given an integer n representing the number of playing cards you have. A house of cards meets the following conditions:
- A house of cards consists of one or more rows of triangles and horizontal cards.
- Triangles are created by leaning two cards against each other.
- One card must be placed horizontally between all adjacent triangles in a row.
- Any triangle on a row higher than the first must be placed on a horizontal card from the previous row.
- Each triangle is placed in the leftmost available spot in the row.
Return the number of distinct house of cards you can build using all n cards. Two houses of cards are considered distinct if there exists a row where the two houses contain a different number of cards.
Example 1:
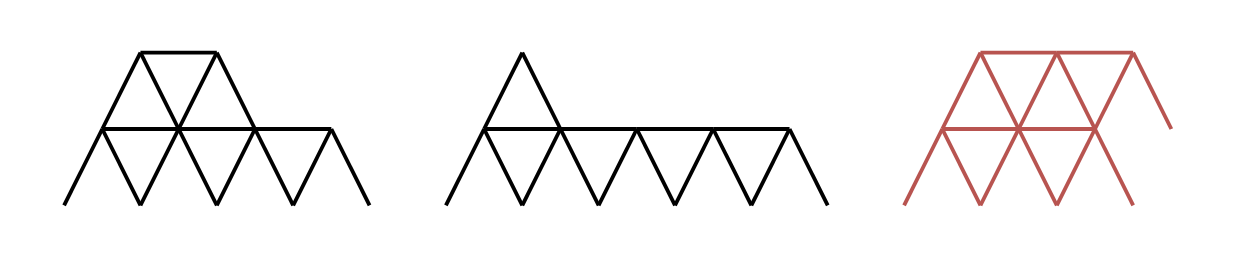
Input: n = 16 Output: 2 Explanation: The two valid houses of cards are shown. The third house of cards in the diagram is not valid because the rightmost triangle on the top row is not placed on top of a horizontal card.
Example 2:

Input: n = 2 Output: 1 Explanation: The one valid house of cards is shown.
Example 3:
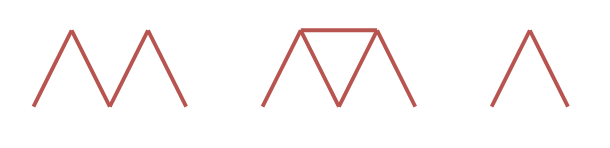
Input: n = 4 Output: 0 Explanation: The three houses of cards in the diagram are not valid. The first house of cards needs a horizontal card placed between the two triangles. The second house of cards uses 5 cards. The third house of cards uses 2 cards.
Constraints:
1 <= n <= 500
题解:
The lower layer must be larger than upper layer.
Say the layer has k triangles, it needs totally 2k + k - 1 cards, which is 3k - 1.
the number of triganles could be 1, 2, 3, 4, 5...
the corresponding card could be 2, 5, 8, 11, 14...
We can see each time it increased by 3.
Now it is like Coin Change II, with value 2, 5, 8, 11, 14... how many ways to make up n. But the difference is each value could only be used once.
Note: i goes down from n to card. Because each value could only be used once. e.g. dp[4], if we go up, dp[2] = 1, dp[4] = dp[2 + 2] = 1, but we know dp [4] should be 0. That is because dp[2] already used value 2.
Time Complexity: O(n ^ 2).
Space: O(n).
AC Java:
1 class Solution { 2 public int houseOfCards(int n) { 3 int[] dp = new int[n + 1]; 4 dp[0] = 1; 5 for(int card = 2; card <= n; card += 3){ 6 for(int i = n; i >= card; i--){ 7 dp[i] += dp[i - card]; 8 } 9 } 10 11 return dp[n]; 12 } 13 }

![[rCore学习笔记 021]多道程序与分时任务](https://img2024.cnblogs.com/blog/3071041/202408/3071041-20240804001732642-496479821.png)