静电场 恒定电流场 知识梳理

前言

最近琢磨了一下Markdown插入LaTeX数学公式，感觉效果确实很不错🧐

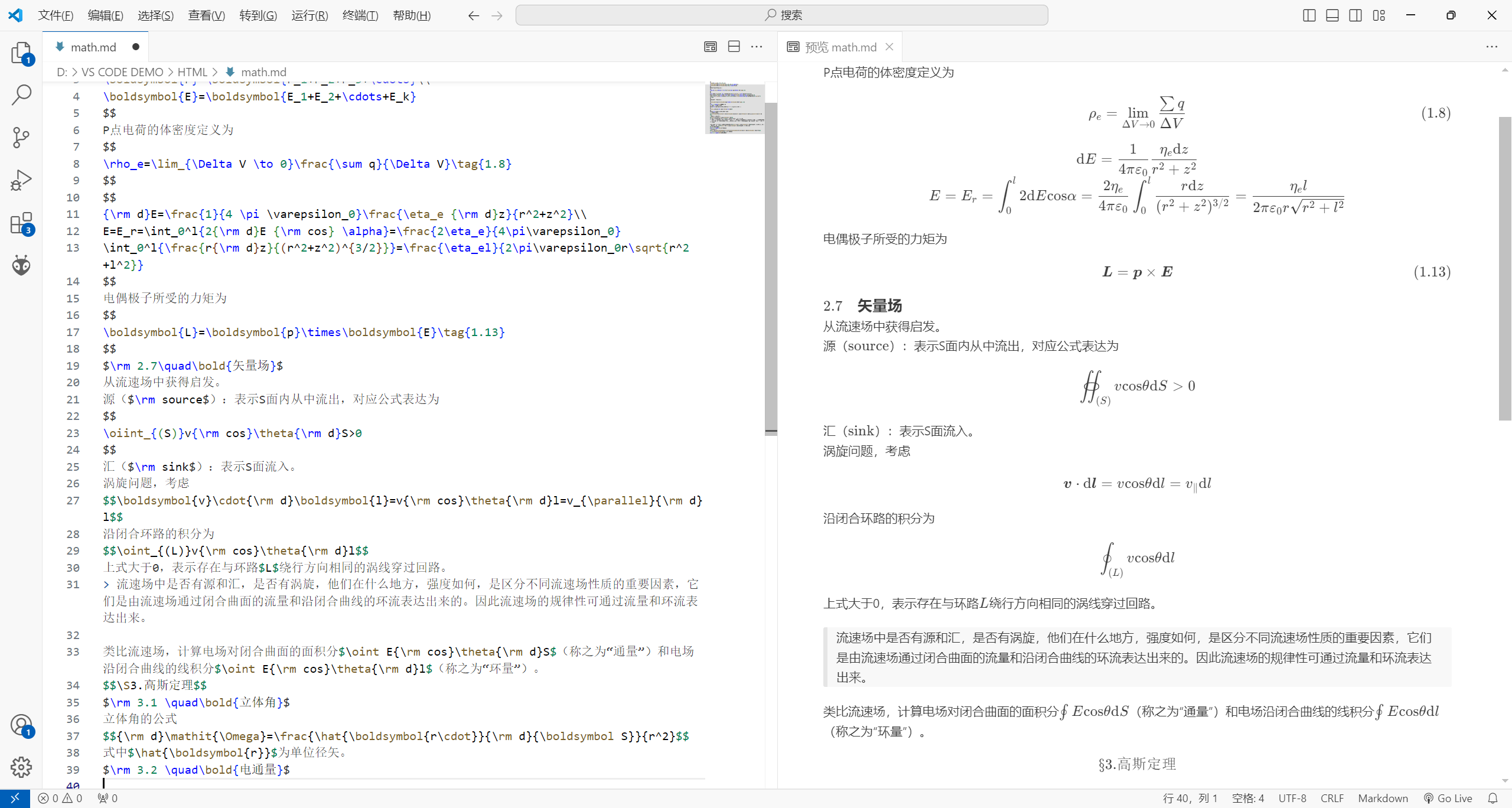
刚好最近比较闲，正想把新概念物理电磁学仔细看一遍，那就拿它来练手好了。下面主要把自己不太熟悉的知识详细解释了一下，比较简单的就一笔带过了。

\[\def\ooint{{\bigcirc}\kern-11.5pt{\int}\kern-6.5pt{\int}} \def\oooint{{\bigcirc}\kern-12.3pt{\int}\kern-7pt{\int}\kern-7pt{\int}} \]

§矢量场

从流速场中获得启发。
源（\(\rm source\)）：表示S面内从中流出，对应公式表达为

\[\ooint_S v \cos \theta{\rm d}S>0 \]

汇（\(\rm sink\)）：表示S面流入。
为了描述涡旋现象，考虑

\[\boldsymbol{v}\cdot{\rm d}\boldsymbol{l}=v\cos\theta{\rm d}l=v_{\parallel}{\rm d}l \]

沿闭合环路的积分为

\[\oint_{(L)}v\cos\theta{\rm d}l \]

上式大于0，表示存在与环路\(L\)绕行方向相同的涡线穿过回路。反过来，上式小于0，表示存在与环路\(L\)绕行方向相反的涡线穿过回路。

流速场中是否有源和汇，是否有涡旋，他们在什么地方，强度如何，是区分不同流速场性质的重要因素，它们是由流速场通过闭合曲面的流量和沿闭合曲线的环流表达出来的。因此流速场的规律性可通过流量和环流表达出来。

类比流速场，计算电场对闭合曲面的面积分\(\oint E\cos\theta{\rm d}S\)（称之为“通量”）和电场沿闭合曲线的线积分\(\oint E\cos\theta{\rm d}l\)（称之为“环量”）。

§高斯定理

立体角

立体角的公式

\[{\rm d}\mathit{\Omega}=\frac{\hat{\boldsymbol{r\cdot}}{\rm d}{\boldsymbol S}}{r^2} \]

式中\(\hat{\boldsymbol{r}}\)为单位径矢。

电通量

定义如下物理量为通过面元\({\rm d}{\boldsymbol S}\)的电通量：

\[{\rm d}{\mathit{\Phi}_E} = E \cos\theta{\rm d}S = \boldsymbol{E\cdot}{\rm d}\boldsymbol{S}\\ \Phi_E=\iint_{(S)}\boldsymbol{E\cdot}{\rm d}\boldsymbol{S} \]

法向矢量的约定：对于闭合曲面，总是取它的外法向矢量。

高斯定理

公式表述

\[\Phi_E=\ooint_{(S)}\boldsymbol{E\cdot}{\rm d}\boldsymbol{S}=\ooint_{(S)}E\cos\theta{\rm d}S=\frac{1}{\varepsilon_0}\sum_i q_i\tag{1.18} \]

其中\(\boldsymbol E\)是带点体系所有电荷（无论是在高斯面内还是高斯面外）产生的总场强，而\(\sum q\)只是对高斯面内的电荷求和，这表明高斯定理表述的内容是高斯面外的电荷对总通量没有贡献，但不是对总场强\(\boldsymbol{E}\)没有贡献。

§电势及其梯度

静电场力所做的功与路径无关。这是静电场的一个很重要的基本性质。另一种等价表述：在静电场中取一任意闭合环路\(L\)，考虑场强\(\boldsymbol{E}\)沿此闭合环路的线积分\(\mathit{\Gamma}_E=\oint\boldsymbol{E\cdot}{\rm d}\boldsymbol{l}\)（\(\mathit{\Gamma}_E\)称为环量）。由于做功与路径无关，故

\[\oint\boldsymbol{E\cdot}{\rm d}\boldsymbol{l}=0\tag{1.28} \]

上式表示，静电场中场强沿任意闭合环路的线积分，即环量恒等于0。我们且把它叫做静电场的环路定理。
电势\(U\)的梯度与电场强度之间的关系为

\[\boldsymbol{E} = -\boldsymbol\nabla U \]

§静电能

我们设想，带电体系中的电荷可以无限分割为许多小部分，这些部分最初都分散在彼此相距很远的位置上。通常规定，处在这种状态下的带电体的静电能为0。进一步，带电体系的静电能\(W_e\)等于把各部分电荷从无限分散的状态聚集成现有带电体系时抵抗静电力所作的全部功\(A'\)。

\[W_e=W_互+W_自 \]

其中：
\(W_e\)：带电体系的总静电能
\(W_互\)：各带电体之间的相互作用能 ，即把每个带电体看作一个不可分割的整体，把各带电体从无限远移到现在位置所作的功。
\(W_自\)：各个带电体的自能，即把各个带电体上的各部分电荷从无限分散的状态聚集起来时所作的功。需要注意的是，不是所有的带电体都有自能一说，例如点电荷和线电荷的自能为无穷大。在这两种情况下只考虑他们的相互作用能。

真空中点电荷的相互作用能

(1)两个点电荷的情形
不妨设将带电体系中的所有点电荷从无穷远处移动到应在的位置，克服静电力做功为\(A'\)，则

\[A'=q_2U_{12}=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{r_{12}} \]

(2)多个点电荷的情形
将上述结果推广到多个点电荷。设点电荷有\(n\)个。依次将这些点电荷由无穷远的地方搬运到它们应在的位置，则搬运各个点电荷的功分别是

\[\begin{cases}A_1'=0,\\A_2'=q_2U_{12},\\A_3'=q_3{(U_{13}+U_{23})},\\\cdots\\A_n'=q_n(U_{1n}+U_{2n}+\cdots+U_{n-1,n}). \end{cases} \]

用通式来表达，则有

\[A_i'=q_i\sum_{j=1}^{i-1}U_{ji},(i=1,2,\cdots,n) \]

其中

\[U_{ji}=\frac{1}{4\pi\varepsilon_0}\frac{q_j}{r_{ij}} \]

建立带电系统的总功为

\[A'=\sum_{i=1}^n A_i'=\sum_{i=1}^n q_i\sum_{j=1}^{i-1}U_{ji}=\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^n\sum_{j=1}^{i-1}\frac{q_iq_j}{r_{ij}} \]

利用对称性，\(A'\)可写成

\[A'=\frac{1}{2}\sum_{i=1}^nq_iU_i\tag{1.59} \]

其中\(U_i\)是除了\(q_i\)以外其余各点在\(q_i\)的位置上产生的电势

\[U_i=\sum_{j=1(j\not ={i})}^n U_{ji} \]

以上是新概念物理中给出的推导过程，实际上通过类似于数学归纳法的方式可以更直观地得到(1.59)式。不管怎么说，最重要的还是最后这一个式子。

连续电荷分布的静电能

推广式(1.59)，以体电荷分布为例,将体电荷无限分割

\[W_e=\frac{1}{2}\sum_i \rho_e\Delta V_i U_i \]

取\(\Delta V_i \to 0\)的极限，有

\[We = \frac{1}{2}\iiint\rho_e U {\rm d}V \]

写出上述积分，就意味着带电体的电荷已经被无限分割，因而得到的也是总静电能\(W_e\)。

面电荷分布的静电能

设面电荷分布密度为\(\sigma_e\)，将面电荷无限分割为圆状面电荷元\(\sigma_e {\rm d}S\)，其自身产生的电势随\({\rm d}S\)趋近于零，总静电能为

\[W_e = \frac{1}{2} \iint_S\sigma_e U {\rm d}S \]

线电荷分布的静电能

注意，不能将线电荷的静电能写为

\[W_e = \frac{1}{2}\int\lambda_e U {\rm d}l \]

这是因为线电荷元\(\lambda_e{\rm d}l\)在自身处产生的电势不仅不零，还会按照\({\rm{ln}}r\)趋于无穷。这在物理上意味着：要把电荷从极端分散状态压缩到一条几何线上，外界需要作无穷大的功。这显然是办不到的。因此，在计算静电能时，无论线径怎样小的带电体均不能当作线电荷处理。《新概念物理：电磁学》的59页直接套用公式给出了线电荷静电能的表达式，可能有误。

多个带电体组成的系统的静电能

设有\(N\)个带电体，则总静电能为

\[W_e=W_互+W_自 \]

如前文所述，点电荷间、线电荷间可以计算互能。但是，不能计算点电荷、线电荷的自能（为无穷大）。

*静电场边值问题的唯一性定理*

表述：
给定各带电体的几何形状、相互位置和下列条件之一：

1. 每个导体的电势\(U_k\)；
2. 每个导体上的总电量\(Q_k\)；

空间里的电场的恒定分布被唯一地确定。

几个引理

 (1)引理一 在无电荷的空间里电势不可能有极大值和极小值。
(2)引理二 若所有导体的电势为0，则导体以外空间的电势处处为0。
(2)引理三 若所有的导体都不带电，则各导体的电势都相等。
由引理二和引理三可以推出，在所有导体都不带电的情况下，空间各处的电势也和导体一样，等于同一常量。

叠加原理

  电势可以直接代数叠加。在给定各导体的几何形状、相互位置后，考虑下面这两种不同的情况：
(1)给定每个导体的电势为\(U_{Ⅰk}\)（或总电量为\(Q_{Ⅰk}\)）
(2)给定每个导体的电势为\(U_{Ⅱk}\)（或总电量为\(Q_{Ⅱk}\)）
在以上这两种条件下，得到的电势分布分别为\(U_{Ⅰ}、U_{Ⅱ}\)。设这两种电势分布的线性组合为\(U=aU_{Ⅰ}+bU_{Ⅱ}\)，那么这一电势分布结果一定反过来对应初始条件：给定每个导体的电势为\(U_k=aU_{Ⅰk}+bU_{Ⅱk}\)。这就是所谓叠加原理。
如果取一个特例：

\[U_{Ⅰk}=U_{Ⅱk},a=1,b=-1 \]

那么线性组合后的电势分布对应的边界条件为

\[U_k=U_{Ⅰk}-U_{Ⅱk}=0 \]

即，给定每个导体的电势为0。

唯一性定理

  (1)给定每个导体电势的情形
不妨假设对于同一组边界条件\(U_k(k=1,2,\cdots)\)（即，第\(k\)个导体的电势为\(U_k\)，这作为边界条件），可以求出两种电势分布\(U_Ⅰ\)和\(U_Ⅱ\)，也就是说空间里的电场分布不唯一。现在取两种电势分布的线性组合

\[U_k=U_{Ⅰk}-U_{Ⅱk} \]

  由于\(U_Ⅰ\)和\(U_Ⅱ\)的边界条件相同，那么\(U_k\)描述的就应当是所有导体上的电势为0的恒定电势分布。再根据上式和引理二，此时空间电势恒等于0，即\(U_Ⅰ\)恒等于\(U_Ⅱ\)。又因为电场强度就是电势的负梯度(\(\boldsymbol{E}=-\boldsymbol\nabla U\))，所以电场分布其实只有唯一解。
(2)给定每个导体上总电量的情形
思路与(1)完全相同，只要先建立起第\(k\)个导体上的总电量\(Q_k\)和电势\(U\)之间的关系

\[Q_k=\varepsilon_0 \oint_{S_k} E_n{\rm d}S = -\varepsilon_0\oint_{S_k} \frac{\partial U}{\partial n}{\rm d}S \]

然后根据引理三推导即可。
把上述证明推广到混合边界条件（即部分导体给定电势、部分给定总电量）的情形是不难的，证明从略。
静电场的唯一性定理的应用：
  静电屏蔽——接地闭合空腔导体把空间分成互不影响的两部分，接地空腔以外空间的场强仅由外部的电荷分布决定，不受内部电荷变化的影响。导体空腔以内空间的场强仅由内部的电荷分布决定，不受外部电荷变化的影响。
电像法

§恒定电流场

电流密度矢量

  单位时间内通过导体任意横截面的电量，叫做电流，记作\(I\)。
电流密度是一个矢量，大小等于通过该点垂直截面的电流。在导体中某点取一个与电流方向垂直的截面元\({\rm d}S\)，则通过\({\rm d}S\)的电流\({\rm d}I\)与该点的电流密度\(j\)的关系是

\[{\rm d }I = j{\rm d}S \]

写成矢量形式

\[{\rm d}I={\boldsymbol{j\cdot}}{\rm d}\boldsymbol{S} \]

或

\[I=\iint_S \boldsymbol{j\cdot}{\rm d}\boldsymbol{S} \]

欧姆定律的微分形式

\[\boldsymbol{j}=\sigma\boldsymbol{E} \]

电流的连续方程

  电流场的一个重要的基本性质是它的连续方程，其实质是电荷守恒定律。
设想在导体内取任一一闭合曲面S，则在某段时间里从这个面流出的电荷量应当等于这段时间里S面内所包含的电量的减少。前者可以通过电流密度矢量\(\boldsymbol j\)积分得到，后者则等于总电荷量\(q\)对时间的变化率，二者数值相等，用数学公式描述为

\[\ooint_S \boldsymbol{j\cdot}{\rm d}\boldsymbol{S}=-\frac{{\rm d}q}{{\rm d}t} \]

  在恒定电流的条件下，电流场不随时间变化，也就是说电荷的分布不随时间变化，即对于任一闭合曲面\(S\)，上式右侧电量对时间的变化率为0。即

\[\ooint_S \boldsymbol{j\cdot}{\rm d}\boldsymbol{S}=0 \]

此式叫做电流的恒定条件。电流线有进入必有对应流出，恒定电流的电流线不可能在任何地方中断，他们永远是闭合曲线（有点像磁力线）。

两种导体分界面上的边界条件

主要是处理不同导电率的大块导体相连的情况。主要的边界条件有两条：

1. 电流密度\(j\)的法向分量连续
2. 电场强度\(\boldsymbol{E}\)的切向分量连续

其中，(1)可以由分界面上电流密度的积分连续得到，(2)可以在分界面上由静电场的环路定理得到。

电流线在导体界面上的折射

电场线与分界面的夹角分别为\(\theta_1\)和\(\theta_2\)，如下图所示

\[j_{1n}=j\cos\theta_1,\quad j_{2n}=j\cos\theta_2 \]

\[E_{1t}=E\sin\theta_1,\quad E_{2t}=E\sin\theta_2 \]

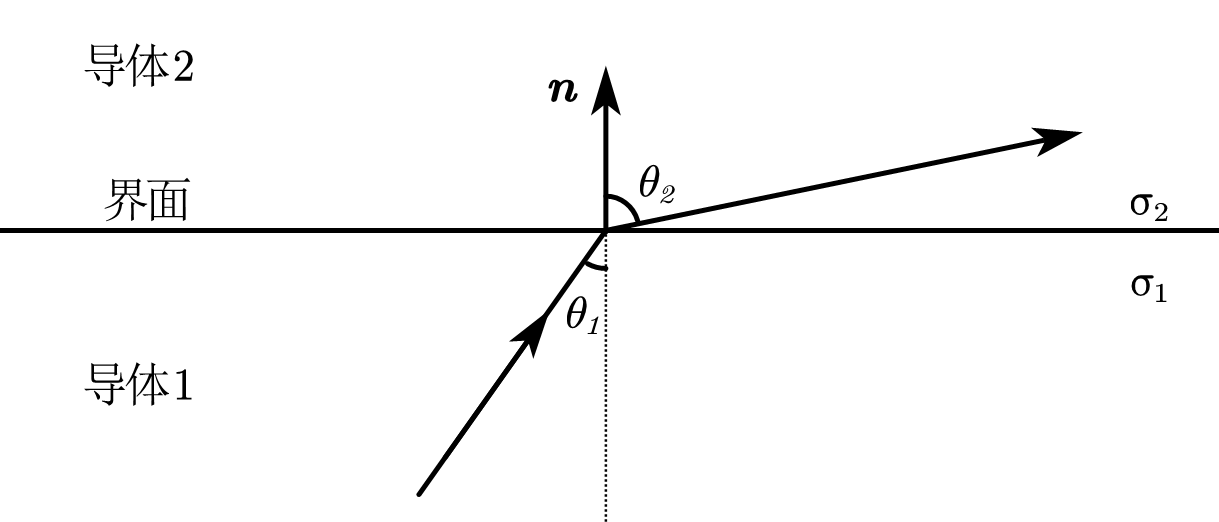
由边界条件得

\[j_{1n}=j_{2n},\quad E_{1t}=E_{2t} \]

两式相除得

\[\frac{E_1}{j_1}\tan\theta_1=\frac{E_2}{j_2}\tan\theta_2 \]

再由欧姆定律得微分形式得

\[\frac{{\rm tan}\theta_1}{{\rm tan}\theta_2} = \frac{\sigma_1}{\sigma_2} \]

即导体界面两侧电流线与法线夹角的正切之比等于两侧电导率之比。一些有趣的推论：如果导体1为不良导体或者绝缘体，导体2为良导体，则在不良导体一侧电流线和电场线几乎与界面垂直，而在良导体一侧电流线和电场线几乎与界面平行，从而电流线非常密集。这样，高导电率的物质就把电流集中到自己内部。