OI学习笔记（C++）

笔记完整版链接（洛谷）——暂无，正在维护

笔记完整版链接（博客）

参照 oi.wiki 整理的一些笔记：

学习笔记+模板（Adorable_hly）

（自己结合网络和做题经验总结的，dalao勿喷）

第一大板块：DP

动态规划适用场景：

1. 最优化原理：若该问题所包含的子问题解是最优的，就称该问题具有最优子结构，满足最优化原理。

2. 无后效性：指某一阶段的状态一旦确定，就不受以后决策的影响，换而言之，某状态不会影响之前的状态，只与当前状态有关。

3. 有重叠子问题：子问题之间不独立，一次决策可能会在往后的决策中多次使用（这一条是动规相较于其他算法的最大优势，是dp的必要条件）。

---

动态规划五大要素：

1. 状态

2. 状态转移方程

3. 普遍决策

4. 初始状态

5. 边界条件

---

背包dp

一，0-1背包

例题（模板）：

题意概要：有 \(n\) 个物品和一个容量为 \(W\) 的背包，每个物品有重量 \(w_{i}\) 和价值 \(v_{i}\) 两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。

对于每种物品，我们有取（1）与不取（0）两种策略，所以称为01背包问题。

状态：设一个 $dp[i][j] → dp_{i,j} $ 数组，表示只考虑前 \(i\) 个物品的情况下（考虑，不一定放，表示最优解），容量为 \(j\) 的背包可以获得的最大总价值。

状态转移方程：对于第i个物品，考虑两种决策：

1. 不放入背包，背包总量保持上一步不变，即 \(dp_{i,j} = dp_{i-1,j}\)

2. 放入背包，背包容量减少 \(w_i\) ，加入新物品的价值 \(v_i\) ,即 \(dp_{i,j} = dp_{i-1,j-w_i} + v_i\)
   综上，可以得出状态转移方程（考虑最优，所以取最大值）

\[dp_{i,j} = max(dp_{i-1,j},dp_{i-1,j-w_i}+v_i) \]

当然，还要加上判断，当 \(j \ge w_i\) 时，才能取决策二，否则 \(dp\) 的第一维可能会变成负数。

但是，如果直接用二维数组表示状态，会 MLE（即爆内存），应考虑用滚动数组的形式来优化（减少一维）。

因为在本题中，状态数组中只有上一次的决策被使用，所以
不用把每次的 \(dp_{i-1,j}\) 都记录下来，可以减少一维，直接用 \(dp_{i}\) 来表示处理到当前物品时背包容量为 \(i\) 的最大价值，得到：

\[dp_{j} = max(dp_{j-1},dp_{j-w_i}+v_i) \]

模板：

for (int i = 1;i<=n;++i)for (int j = W;j>=w[i];--j) //不要写递增的f[j] = max(f[j],f[j - w[i]] + v[i]);

二，完全背包

与01背包类似，不同点在于完全背包每件物品有无限个，即可以选无限次，二01背包每件物品只能选一次。

状态：设 \(dp_{i,j}\) 为只能选前 i 个物品时，容量为 j 的背包可以达到的最大价值。

最暴力的 \(dp\) 就是和0-1背包思路差不多的， \(k\) 为拿的数量，一个个枚举来转移，方程如下：

\[dp_{i,j}=\max_{k=0}^{+\infty}(dp_{i-1,j-k\times w_i}+v_i\times k) \]

这个做法的复杂度为：\(O(n^3)\)

---

↑ 理解了， ↓ 没理解

---

考虑一下优化，引用自 oi.wki-完全背包 (略微改动)

没理解优化，但是还是背下来吧:

---

考虑做一个简单的优化。可以发现，对于 \(f_{i,j}\)，只要通过 \(f_{i,j-w_i}\) 转移就可以了。因此状态转移方程为：

\[dp_{i,j}=\max(dp_{i-1,j},dp_{i,j-w_i}+v_i) \]

理由是当我们这样转移时，\(dp_{i,j-w_i}\) 已经由 \(dp_{i,j-2\times w_i}\) 更新过，那么 \(dp_{i,j-w_i}\) 就是充分考虑了第 i 件物品所选次

例题（模板）：

题意概要：有 \(n\) 种物品和一个容量为 \(W\) 的背包，每种物品有重量 \(w_{i}\) 和价值 \(v_{i}\) 两种属性，要求选若干个物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。

例题代码
#include<bits/stdc++.h>
using namespace std;const int maxn = 1e4+5,maxm = 1e7+5;
int n, W, w[maxn], v[maxn];
long long dp[maxm];int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);cin>>W>>n;for(int i = 1; i<=n;++i) cin>>w[i]>>v[i];for(int i = 1; i<=n;++i)for(int j = w[i];j<=W;j++)if(dp[j-w[i]]+v[i]>dp[j]) dp[j]=dp[j-w[i]]+v[i];cout<<dp[W]<<endl;return 0;
}

---

三，多重背包

从多重背包是0-1背包的变式，多重背包每种物品有 \(k_i\) 个，不是一个。

朴素的想法：把「每种物品选 \(k_i\) 次」等价转换为「有 \(k_i\) 个相同的物品，每个物品选一次」。就成了01背包的板子
状态转移方程：

\[dp_{i,j}=\max_{k=0}^{k_i}(dp_{i-1,j-k\times w_i}+v_i\times k) \]

时间复杂度为 $ O(W\sum_{i=1}^nk_i)$ 。

模板：

for(int i = 1;i<=n;++i)for(int weight = W;weight>=w[i];--weight)for(int k = 1;k*w[i]<=weight && k<=cnt[i];++k)dp[weight] = max(dp[weight],dp[weight-k*w[i]]+v[i]*k);

这个方法的复杂度还是不低的，我们考虑优化：
我看不懂，粘一下 oi.wiki 上的解释：

二进制分组优化：

考虑优化。我们仍考虑把多重背包转化成 0-1 背包模型来求解。

显然，复杂度中的 \(O(nW)\) 部分无法再优化了，我们只能从 \(O(\sum k_i)\) 处入手。为了表述方便，我们用 \(A_{i,j}\) 代表第 i 种物品拆分出的第 \(j\) 个物品。

在朴素的做法中，\(\forall j\le k_i，A_{i,j}\) 均表示相同物品。那么我们效率低的原因主要在于我们进行了大量重复性的工作。举例来说，我们考虑了「同时选 \(A_{i,1},A_{i,2}\)」与「同时选 \(A_{i,2},A_{i,3}\)」这两个完全等效的情况。这样的重复性工作我们进行了许多次。那么优化拆分方式就成为了解决问题的突破口。

过程
我们可以通过「二进制分组」的方式使拆分方式更加优美。

具体地说就是令 \(A_{i,j}\left(j\in\left[0,\lfloor \log_2(k_i+1)\rfloor-1\right]\right)\) 分别表示由 2\(^{j}\) 个单个物品「捆绑」而成的大物品。特殊地，若 \(k_i+1\) 不是 \(2\) 的整数次幂，则需要在最后添加一个由 \(k_i-2^{\lfloor \log_2(k_i+1)\rfloor-1}\) 个单个物品「捆绑」而成的大物品用于补足。

举几个例子：

\(6 =1+2+3\)
\(8 = 1+2+4+1\)
\(18 = 1+2+4+8+3\)
\(31 = 1+2+4+8+16\)

显然，通过上述拆分方式，可以表示任意 \(\le k_i\) 个物品的等效选择方式。将每种物品按照上述方式拆分后，使用 0-1 背包的方法解决即可。

时间复杂度 \(O(W\sum_{i=1}^n\log_2k_i)\)。

二进制分组代码 （看不懂） :

index = 0;
for(int i = 1;i<=m;++i)
{int c = 1,p,h,k;cin>>p>>h>>k;while(k>c){k -= c;list[++index].w = c * p;list[index].v = c * h;c *= 2;}list[++index].w = p*k;list[index].v = h*k;
}

---

dp未完待续……

---

------------------------华丽的分割线---------------------------

---

第二大板块：树状数组

一，概念
手搓了两张草图：
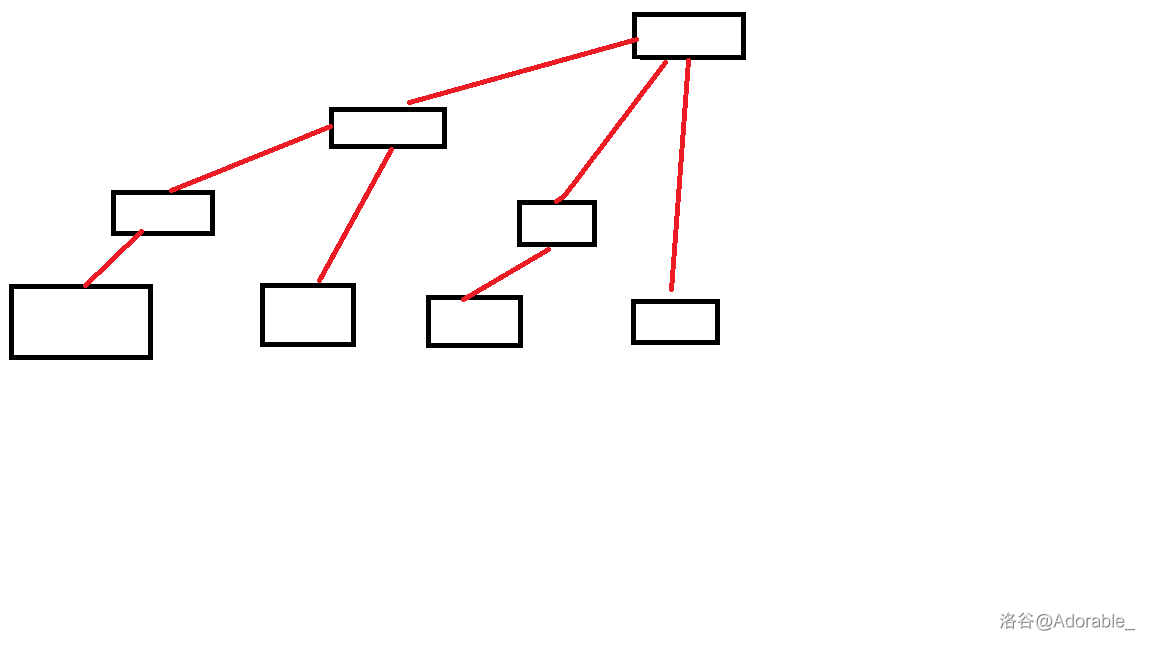图一 ↑ ↑ ↑

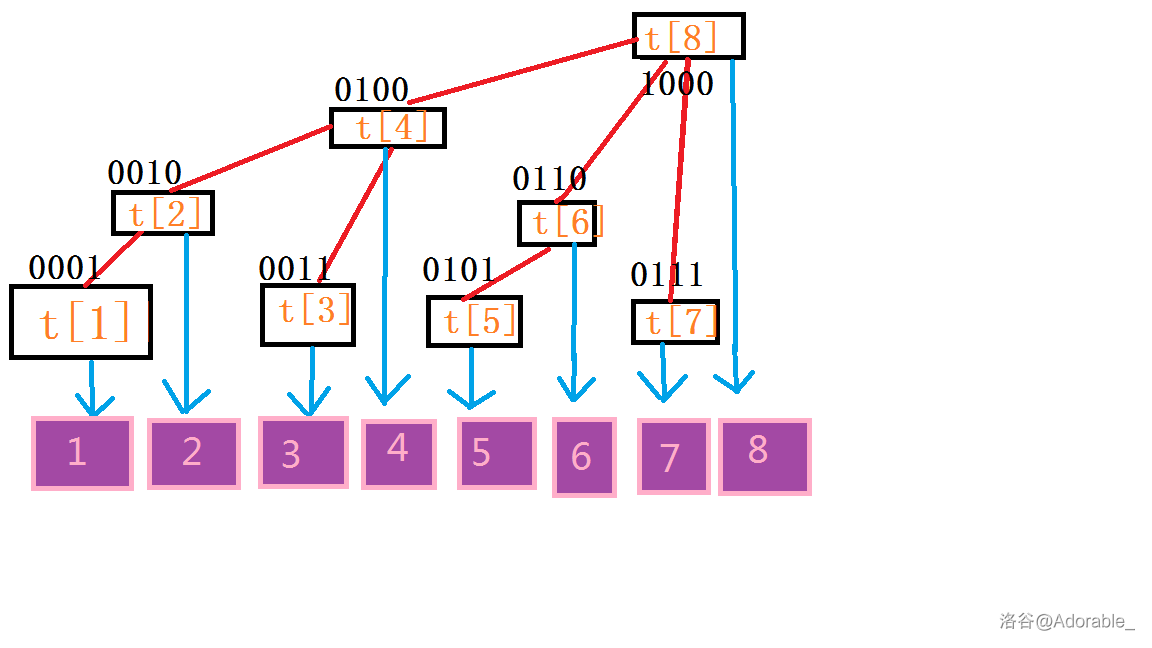图二 ↑ ↑ ↑（请不要在意颜色，瞎整的）

关于储存大概就是这个结构，和线段树的功能有点像。

• 功能：

1. 单点修改，单点查询(这个就不要需要树状数组了)
2. 区间修改，单点查询（本版块重点）
3. 单点修改，区间查询（本版块重点）
4. 区间修改，区间查询（建议线段树实现）
5. 等等

优点：相较于线段树好写，省时省力（杀鸡焉用宰牛刀， 而且我现在也不会线段树 ）。

缺点：扩展性弱，换而言之，线段树能解决的问题用树状数组可以解决大部分，但不是全部。

先记一下 lowbit 的用法：

计算非负整数 n 在二进制下，从右到左第一个1到最右边构成的数，等价于删去从左到右最后一个1到最左边所有的数（最后一个1不删）

例如：

a = 1010100;
lowbit(a) = 100;//删去了左边的“1010”

• 实现：对 \((x)_2\) 取反，再与原数 \((x)_2\) 进行按位与运算。

• 写法1：

int lowbit(int x)
{ return ((x)&(-x)); }//因为篇幅，稍微压一下行

• 写法2：

#define lowbit(x) ((x)&(-x))

注：带一堆括号只是为了保险 （虽然我也知道没必要，但写上肯定不会错）

如图2，用t[i]表示以x为根的子数中叶子节点值的和，原数组为a[]。容易发现：

\[t_4 = t_2+t_3+a_4 = t_1+a_2+t_3+a_4 = a_1+a_2+a_3+a_4 \]

观察一下二进制数，发现每一层末尾的0个数是相通的（可能我画的不太形象，第一层是 \(t_1,t_3,t_5,t_7\),第二层是 \(t_2,t_6\) ,第三层是 \(t_4\) ,第四层是 \(t_8\) ）

再观察，树状数组中节点x的父亲节点为 x + lowbit(x)
eg:对于 t[2] (父亲节点为 t[4] )，

\[t[4] = t[2+lowbit(2)] , 4 = 2+lowbit(2) \]

原理大致介绍完了，记一下例题吧

例题

洛谷P3374 树状数组模板1

---

• 大意：输入n，m（该数列数字的个数和操作的总个数）
  输入n个数表示第 i 项的初始值。
  接下来 m 行每行包含 3 个整数，表示一个操作:
  1 x k 含义：将第 x 个数加上 k
  2 x y 含义：输出区间 [x,y] 内每个数的和

对于每次2操作输出一次区间和。

---

一道很板的题，要考虑两个：单点修改和区间查询

1. 单点修改，区间查询

1.1 单点修改

单点修改时，可以吧 t[i]理解为前缀和，例如，如果我们对 a[1]+k，那么对于 t[1],t[2],t[4],t[8]（即全部祖先）都需要+k更新，此时就可以使用上面关于 lowbit 的结论了，

• 模板：

int add(int x,int k)//对第x项进行+k操作
{for(int i = x;i<=n;i+=lowbit(i))t[i]+=k;
}

1.2 区间查询

我们先找例子，再由一般到特殊：
eg:查询 1~7的和

还是从图2，很容易看出：答案就是 \(t[7]+t[6]+t[4]\)

进一步观察，

\[6 = 7-lowbit(7),4 = 6-lowbit(6) \]

所以可以循环不断 -lowbit(),一直减到最底层来实现

int sumout(x)
{int sum = 0;for(int i=x;i;i-=lowbit(i))sum+=t[i];return sum;
}//算了压行码风太丑，就不了。。。

这个模板只能求区间 [1，x] 的和，当然求 [l,r] 的区间和基本同理，利用前缀和相减的性质就可以了，

\[[l,r] = [1,r]-[1,l-1] \]

• 实现1：
  利用上述函数

return sumout(1,r)-sumout(1,l-1);

• 实现2：

重新手搓一个
也是前缀和思想，同上

int sumout(int l,int r)
{int sum = 0;for(int i = r;i;i-=lowbit(i)) sum+=t[i];for(int i = l-1;i;i-=lowbit(i)) sum-=t[i];return sum;
}

洛谷P3368 树状数组模板2

2. 区间修改，单点查询

2.1 区间修改

差分的原理，构造一个差分数组 c，用树状数组维护 c 即可，利用差分数组的性质，只需要更新 \(add(l,k),add(r+1,-k)\) 即可

• 模板：

void change(int loc,int k)//把loc及其后面的点+k
{for(int i = loc;i<=n;i+=lowbit(i))c[i]+=k;
}

• 实现：

change(l,k);
change(r+1,-k);

2.2 单点查询

单点查询即求出 c 的前缀和即可；

\(a[x] = c[1] + c[2] + ... + c[x]的前缀和\)（依据差分数组的性质）

int findd(int loc)
{int ans = 0;for(int i = loc;i;i-=lowbit(i)) ans+=c[i];return ans;
}

lowbit 原理同上

3.区间修改，区间查询

用树状数组过于复杂，建议使用线段树 （虽然我不会）
你好我叫郭旭东

---

------------------------华丽的分割线---------------------------

---

第三大板块：图论

先整理一下基本概念（部分引用自 oi.wiki ）

只介绍比较简单的定义：

图（graph）是一个二元组 \(G = (V(G),E(G))\)。其中 V(G) 是非空集，称为 点集 (vertex set)，对于 V 中的每个元素，我们称其为 顶点 (vertex) 或 节点 (node)，简称 点；E(G) 为 V(G) 各结点之间边的集合，称为 边集 (edge set)。

常用 G=(V,E) 表示图。
当 V,E 都是有限集合时，称 G 为 有限图。
当 V 或 E 是无限集合时，称 G 为 无限图。

若 G 为无向图，则 E 中的每个元素为一个无序二元组 (u, v)，称作 无向边 (undirected edge)，简称 边 (edge)，其中 u, v \in V。设 e = (u, v)，则 u 和 v 称为 e 的 端点 (endpoint)。

若 G 为有向图，则 E 中的每一个元素为一个有序二元组 (u, v)，有时也写作 u \(\to\) v，称作 有向边 (directed edge) 或 弧 (arc)，在不引起混淆的情况下也可以称作 边 (edge)。设 e = u \(\to\) v，则此时 u 称为 e 的 起点 (tail)，v 称为 e 的 终点 (head)，起点和终点也称为 e 的 端点 (endpoint)。并称 u 是 v 的直接前驱，v 是 u 的直接后继。

若 G 为混合图，则 E 中既有 有向边，又有 无向边。

若 G 的每条边 e_k=(u_k,v_k) 都被赋予一个数作为该边的 权，则称 G 为 赋权图。如果这些权都是正实数，就称 G 为 正权图。

形象地说，图是由若干点以及连接点与点的边构成的。

路径

\(途径 (walk)：途径是连接一连串顶点的边的序列，可以为有限或无限长度。形式化地说，一条有限途径 w 是一个边的序列 e_1, e_2, \ldots, e_k，使得存在一个顶点序列 v_0, v_1, \ldots, v_k 满足 e_i = (v_{i-1}, v_i)，其中 i \in [1, k]。这样的途径可以简写为 v_0 \to v_1 \to v_2 \to \cdots \to v_k。通常来说，边的数量 k 被称作这条途径的 长度（如果边是带权的，长度通常指途径上的边权之和，题目中也可能另有定义）。\)

\(迹 (trail)：对于一条途径 w，若 e_1, e_2, \ldots, e_k 两两互不相同，则称 w 是一条迹。\)

\(路径 (path)（又称 简单路径 (simple path)）：对于一条迹 w，若其连接的点的序列中点两两不同，则称 w 是一条路径。回路 (circuit)：对于一条迹 w，若 v_0 = v_k，则称 w 是一条回路。\)

\(环/圈 (cycle)（又称 简单回路/简单环 (simple circuit)）：对于一条回路 w，若 v_0 = v_k 是点序列中唯一重复出现的点对，则称 w 是一个环。\)

连通

无向图

对于一张无向图 G = (V, E)，对于 u, v \in V，若存在一条途径使得 v_0 = u, v_k = v，则称 u 和 v 是 连通的 (connected)。由定义，任意一个顶点和自身连通，任意一条边的两个端点连通。

若无向图 G = (V, E)，满足其中任意两个顶点均连通，则称 G 是 连通图 (connected graph)，G 的这一性质称作 连通性 (connectivity)。

若 H 是 G 的一个连通子图，且不存在 F 满足 H\subsetneq F \subseteq G 且 F 为连通图，则 H 是 G 的一个 连通块/连通分量 (connected component)（极大连通子图）。

有向图

对于一张有向图 G = (V, E)，对于 u, v \in V，若存在一条途径使得 v_0 = u, v_k = v，则称 u 可达 v。由定义，任意一个顶点可达自身，任意一条边的起点可达终点。（无向图中的连通也可以视作双向可达。）

若一张有向图的节点两两互相可达，则称这张图是 强连通的 (strongly connected)。

若一张有向图的边替换为无向边后可以得到一张连通图，则称原来这张有向图是 弱连通的 (weakly connected)。

与连通分量类似，也有 弱连通分量 (weakly connected component)（极大弱连通子图）和 强连通分量 (strongly connected component)（极大强连通子图）。

相关算法请参见 强连通分量。

割

相关算法请参见 割点和桥 以及 双连通分量。

在本部分中，有向图的「连通」一般指「强连通」。

对于连通图 G = (V, E)，若 V'\subseteq V 且 G\left[V\setminus V'\right]（即从 G 中删去 V' 中的点）不是连通图，则 V' 是图 G 的一个 点割集 (vertex cut/separating set)。大小为一的点割集又被称作 割点 (cut vertex)。

对于连通图 G = (V, E) 和整数 k，若 |V|\ge k+1 且 G 不存在大小为 k-1 的点割集，则称图 G 是 k- 点连通的 (k-vertex-connected)，而使得上式成立的最大的 k 被称作图 G 的 点连通度 (vertex connectivity)，记作 \kappa(G)。（对于非完全图，点连通度即为最小点割集的大小，而完全图 K_n 的点连通度为 n-1。）

对于图 G = (V, E) 以及 u, v\in V 满足 u\ne v，u 和 v 不相邻，u 可达 v，若 V'\subseteq V，u, v\notin V'，且在 G\left[V\setminus V'\right] 中 u 和 v 不连通，则 V' 被称作 u 到 v 的点割集。u 到 v 的最小点割集的大小被称作 u 到 v 的 局部点连通度 (local connectivity)，记作 \kappa(u, v)。

还可以在边上作类似的定义：

\(对于连通图 G = (V, E)，若 E'\subseteq E 且 G' = (V, E\setminus E')（即从 G 中删去 E' 中的边）不是连通图，则 E' 是图 G 的一个 边割集 (edge cut)。大小为一的边割集又被称作 桥 (bridge)。\)

\(对于连通图 G = (V, E) 和整数 k，若 G 不存在大小为 k-1 的边割集，则称图 G 是 k- 边连通的 (k-edge-connected)，而使得上式成立的最大的 k 被称作图 G 的 边连通度 (edge connectivity)，记作 \lambda(G)。（对于任何图，边连通度即为最小边割集的大小。）\)

\(对于图 G = (V, E) 以及 u, v\in V 满足 u\ne v，u 可达 v，若 E'\subseteq E，且在 G'=(V, E\setminus E') 中 u 和 v 不连通，则 E' 被称作 u 到 v 的边割集。u 到 v 的最小边割集的大小被称作 u 到 v 的 局部边连通度 (local edge-connectivity)，记作 \lambda(u, v)。\)

点双连通 (biconnected)

\(几乎与 2- 点连通完全一致，除了一条边连接两个点构成的图，它是点双连通的，但不是 2- 点连通的。换句话说，没有割点的连通图是点双连通的。\)

边双连通 (2-edge-connected)

\(与 2- 边双连通完全一致。换句话说，没有桥的连通图是边双连通的。\)

\(与连通分量类似，也有 点双连通分量 (biconnected component)（极大点双连通子图）和 边双连通分量 (2-edge-connected component)（极大边双连通子图）。\)

Whitney 定理：

\(对任意的图 G，有 \kappa(G)\le \lambda(G)\le \delta(G)。（不等式中的三项分别为点连通度、边连通度、最小度。）\)

其他更详细的 森林 之类的，详情见 OI.WIKI-图论相关概念

1.0 图的存储

1.1 直接存边

使用一个数组来存边，数组中的每个元素都包含一条边的起点与终点（带边权的图还包含边权）。（或者使用多个数组分别存起点，终点和边权。）

模板：

#include<bits/stdc++.h>
using namespace std;struct Edge
{int u, v;
};
int n, m;
vector<Edge> e;
vector<bool> vis;bool find_edge(int u, int v)
{for(int i = 1; i <= m; ++i){if(e[i].u == u && e[i].v == v){return true;}}return false;
}
void dfs(int u)
{if(vis[u]) return;vis[u] = true;for(int i = 1;i<=m;++i)if(e[i].u == u)dfs(e[i].v);
}
int main()
{cin>>n>>m;vis.resize(n + 1,0);e.resize(m + 1);for(int i = 1; i <= m; ++i) cin>>e[i].u>>e[i].v;return 0;
}

复杂度：

查询是否存在某条边： \(O(m)\) 。

遍历一个点的所有出边： \(O(m)\) 。

遍历整张图： \(O(nm)\) 。

空间复杂度： \(O(m)\) 。

1.2 邻接矩阵：

用edge[][]来储存边，若 u 到 v 存在边，让 edge[u][v] = 1 ，反之设为 0 ，若图存在边权，可以直接储存边权。
模板：

#include<bits/stdc++.h>
using namespace std;const int N = 1e5+5;
bool edge[N][N];
int m;int main()
{cin>>m;for (int i = 1;i<=m;++i){int u, v;cin>>u>>v;edge[u][v] = 1;}return 0;
}
//带边权版本 
#include<bits/stdc++.h>
using namespace std;const int N = 1e5+5;
int edge[N][N];
int m;int main()
{cin>>m;for (int i = 1;i<=m;++i){int u,v,w;cin>>u>>v>>w;edge[u][v] = w;}return 0;
}
/*
遍历·摘自oi.wiki 
void dfs(int u) {if (vis[u]) return;vis[u] = true;for (int v = 1; v <= n; ++v) {if (adj[u][v]) {dfs(v);}}
}
*/

复杂度：

查询是否存在某条边： \(O(1)\) 。

遍历一个点的所有出边： \(O(n)\) 。

遍历整张图： \(O(n^2)\) 。

空间复杂度： \(O(n^2)\) 。

1.3 链式前向星

实质：链表

实现：

void add(int u, int v)
{nxt[++cnt] = head[u];  // 当前边的后继head[u] = cnt;         // 起点 u 的第一条边to[cnt] = v;           // 当前边的终点
}

遍历 u 的出边：

for (int i = head[u]; i!=-1; i = nxt[i])
{int v = to[i];
}

模板：

#include<bits/stdc++.h> 
using namespace std;int n,m;
vector<bool> vis;
vector<int> head, nxt, to;void add(int u,int v)
{nxt.push_back(head[u]);head[u] = to.size();to.push_back(v);
}
bool find_edge(int u,int v)
{for(int i = head[u];i!=-1;i = nxt[i])if(to[i] == v)return true;return false;
}
void dfs(int u)
{if(vis[u]) return;vis[u] = true;for(int i = head[u]; ~i; i = nxt[i]) dfs(to[i]); //~i 等效 i!=-1
}int main()
{cin>>n>>m;vis.resize(n + 1,false);head.resize(n + 1,-1);for(int i = 1;i<=m;++i){int u, v;cin>>u>>v;add(u,v);}return 0;
}

复杂度:

查询是否存在 u 到 v 的边： \(O(d^+(u))\) 。

遍历点 u 的所有出边： \(O(d^+(u))\) 。

遍历整张图： \(O(n+m)\) 。

空间复杂度： \(O(m)\) 。

2.0 最短路算法

记号：
为了方便叙述，这里先给出下文将会用到的一些记号的含义。

• \(n\) 为图上点的数目，\(m\) 为图上边的数目；

• \(s\) 为最短路的源点；

• \(D(u)\) 为 \(s\) 点到 \(u\) 点的 实际 最短路长度；

• \(dis(u)\) 为 \(s\) 点到 \(u\) 点的估计最短路长度。任何时候都有 \(dis(u) \geq D(u)\)。特别地，当最短路算法终止时，应有 \(dis(u)=D(u)\)。

• \(w(u,v)\) 为 \((u,v)\) 这一条边的边权。

性质：

对于边权为正的图，有：

1. 任意两个结点之间的最短路，不会经过重复的结点。
2. 任意两个结点之间的最短路，不会经过重复的边。
3. 任意两个结点之间的最短路，任意一条的结点数不会超过 \(n\)，边数不会超过 \(n-1\)。

2.1 \(Floyd\) 算法

特点：

复杂度高，常熟小，易实现。

使用场景：

不能有负环，必须存在负环且不被有无向和边权正负影响

实现：

定义一个数组：\(f[k][x][y]\)，表示只允许经过结点 \(1\) 到 \(k\)（也就是说，在子图 \(V'={1, 2, \ldots, k}\) 中的路径，注意，\(x\) 与 \(y\) 不一定在这个子图中），结点 \(x\) 到结点 \(y\) 的最短路长度。

所以节点 \(x\) 到 \(y\) 的最短距离就是 \(f[n][x][y]\)。

f[0][x][y]：\(x\) 与 \(y\) 的边权，或者 \(0\) 或者 \(+\infty\)
（当 \(x = y\) 的时候为零，因为到本身的距离为零；当 \(x\) 与 \(y\) 没有直接相连的边的时候，为 \(+\infty）\)。）

所以公式就是：

\[f[k][x][y] = min(f[k-1][x][y],f[k-1][x][k]+f[k-1][k][y]) \]

因为第一维的参数只会使用到k-1，可以使用滚动数组优化掉一维。

即为：

\[f[x][y] = f[x][k]+f[k][y] \]

时间复杂度为：\(O(n^3)\)

模板：

for(int k = 1;k<=n;k++){for(int x = 1;x<=n;x++){for(int y = 1;y<=n;y++){f[x][y] = min(f[x][y], f[x][k] + f[k][y]);}}
}

.