做题小结 dp训练4

第一个

我按dp找 结果是个二分 我还想半天 这怎么dp
不过 这题目 也很有意义

首先我一直以为vector的low或者upp下标只能用distance求
现在看来是错的 不要再写auto 迭代器写法 用int就行 减初始指针就行

然后二分的话 思路也很好

先存进去 然后在跑t的时候 先开一个指针 然后对于一个字符判断当前指针与他的下标对比 发现够用更新指针 不够用ans++ 更新指针即可
非常好的一道二分

树形dp

这是我自己想出来的 ac了感觉很开心
首先这是一颗二叉树

然后思考dp如何建立

对于一个节点而言
如果他有两个孩子 那么我们要算出他和孩子的总数
还要算出最大儿子子树的数量 还要算出如果切这个枝条那他的贡献（记住-1）
一个孩子的话 没得选
所以我们开二维表示

//0 自己子树的所有节点数  
//1 表示其中某个节点的最大儿子数   
//2 表示选择了一颗子树后，
//另一颗子树选了其中一颗最大子树后的值 dp[u][0]=1;dp[u][1]=0;dp[u][2]=0;for(auto v:e[u]){if(v==fa)continue;dfs(v,u);dp[u][0]+=dp[v][0];dp[u][1]=max(dp[u][1],dp[v][0]);//删的是u 不是儿子 		}

下面就开始分析孩子 一个孩子的话 就只好选下去了

	int w;if(u==1)w=e[u].size();else  w=e[u].size()-1;if(w==1){int one=0;for(auto i:e[u]){if(i!=fa)one =i;}dp[u][2]=dp[one][0]-1;}

这边细节蛮多的

	if(i!=fa)one =i;一开始没想到 后面看答案有问题才调出来 

两个的

	else if(w==2){int one=0,two=0;for(auto i:e[u]){if(i!=fa&&!one)one=i;else if(i!=fa&&one)two=i;}
感觉自己太牛逼了 if(dp[one][0]+dp[two][2]>dp[two][0]+dp[one][2]){dp[u][2]=dp[one][0]+dp[two][2]-1;}else {dp[u][2]=dp[two][0]+dp[one][2]-1;}}	

压轴登场

神题

首先给出我的思路 我开了个三维dp
二维表示此时a选的 三维表示此时b选的
发现要4个for循环吧 反正肯定要超时 然后我也没想优化
主要是脑子也没优化的概念 看了题解才知道可以优化

		for (jt=1;jt<=n;jt++)for (j2=n;j2>=jt;j2--)for (j3=1;j3<=jt;j3++)for (j4=max(j3,j2);j4<=n;j4++)f[i][jt][j2]+=f[i-1][j3][j4];

那么我们该怎么优化呢 我们可以使用二维前缀和的思想
我们令sum[n][i][j]表示小于等于i 大于等于j的所有方案
那么可以怎么转移呢 很明显 我们可以由i-1 j ,i j+1 转移过来
其实二维前缀和转移 为什么j+1是因为我们毕竟算大于等于j
和j-1无关 然后你会发现重复了一段 i-1 j+1 因为二者都包含了这个
所以减去 然后呢 我们还要加上此前就有的n-1 i j 因为可以等于嘛

提前预处理1的值 后续转移要用

cin>>n>>m;for(int i=1;i<=n;i++){		for(int j=n;j>=i;j--){//i是a j是b j必须大于ie[1][i][j]=(e[1][i-1][j]+e[1][i][j+1]+mod-e[1][i-1][j+1]+1+mod)%mod;//二维前缀和 dp[1][i][j]=1;	//n=1 就不怕了 		}}for(int i=2;i<=m;i++){for(int j=1;j<=n;j++){for(int k=n;k>=j;k--){//这一步很重要dp[i][j][k]=e[i-1][j][k];e[i][j][k]=(((e[i][j-1][k]+e[i][j][k+1])%mod-e[i][j-1][k+1]+mod)%mod+e[i-1][j][k]+mod)%mod;	
要累加 所以是i	  }}}int ans=0;for(int i=1;i<=n;i++){for(int j=n;j>=i;j--){ans=(ans+dp[m][i][j])%mod;}}cout<<ans<<endl;

第二种 固定长度不下降序列的写法
可以观察到其实就是一个

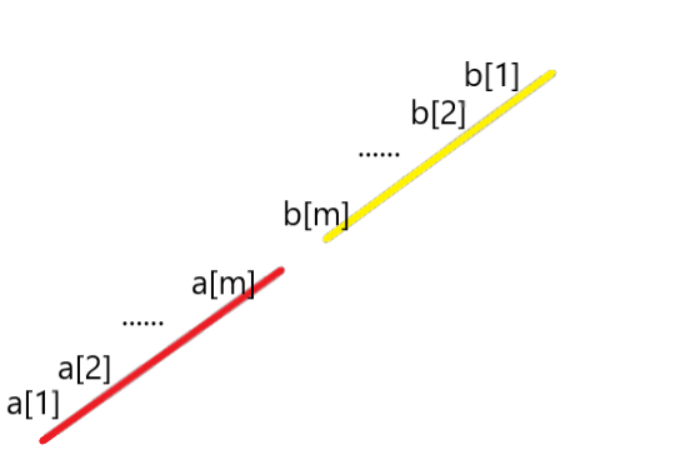
写要怎么写呢
先m*2
dp数组表示第i位以j结尾
加上选j 那么j-1我们是要知道 j也是要知道

所以开一个sum记录 i-1以j结尾的 i-1以j结尾的答案 当然此时dp是等于
i-1 j-1 因为此时选的j嘛 不过sum要加上去 毕竟是前缀和

int n;int m;
int a[range];
int mod=1e9+7;
int dp[1005][1005];
int sum[1005][1005];
void solve()
{ //open my eyes in morning rain//Clouds are slowly drifting by who is crying under the skycin>>n>>m;m=2*m;sum[0][0]=1;int ans=0;for(int i=1;i<=n;i++){dp[1][i]=1;sum[1][i]=sum[1][i-1]+1;}for(int i=2;i<=m;i++){for(int j=1;j<=n;j++){			dp[i][j]=sum[i-1][j];//i-1以j结尾 sum[i][j]=(dp[i][j]+sum[i][j-1])%mod;//表示i位时所有小于等于j的方案数 }}//跟我第一个写法好像啊 这个写法 不过更简便了 
//	cout<<m<<endl;for(int i=1;i<=n;i++){
//	 cout<<dp[m][i]<<endl;ans=(ans+dp[m][i])%mod;}	cout<<ans<<endl;
}

写完了 休息下吧