六、决策树-编程知识

六、决策树

news/2024/11/16 18:30:25/文章来源:https://www.cnblogs.com/pgl6/p/18351028

决策1：如何选择在每个节点上分割什么特征？

最大限度地提高纯度（或最小限度地减少不纯）。

决策2：什么时候停止拆分？

当一个节点是一个单一类时
当拆分一个节点会导致树超过最大的深度
当纯度分数的改进低于一个阈值（获得的信息增益很小小于阈值）
当一个节点中的例子数量低于一个阈值

6.1 衡量纯度、熵entropy、Gini指数

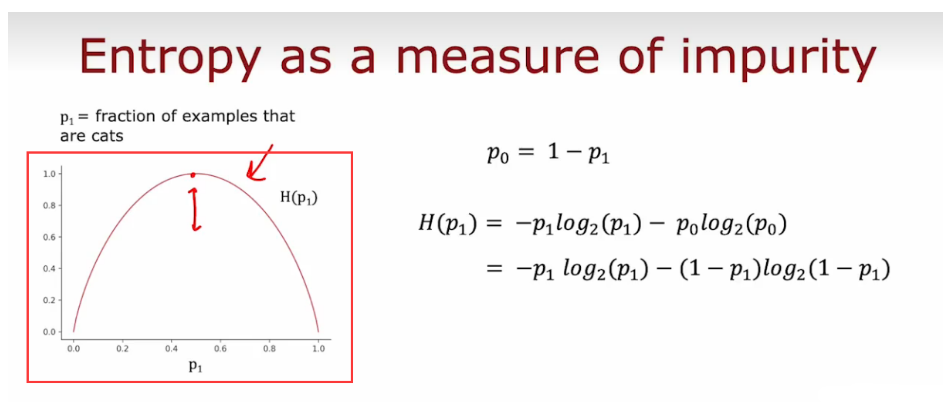
熵（Entropy）通常用于衡量样本集合的不确定性和纯度，也可以理解为样本集合中随机选取一个样本，其所包含的信息量，混乱程度。

可以发现，当正例和反例比例相等时，即p₊ = p₋ = 0.5 时，此时的熵取最大值1，表明此时样本集合最不确定，样本集合越不纯，熵值越大；而当样本集合中只包含一类样本（即纯样本集合）时，熵值为0，表明此时样本集合已经完全确定，很纯。
在决策树算法中，熵常常被用来选择最优划分点，即在样本的某个特征上根据熵的变化选取最优的划分点，使得划分后的样本子集中的熵最小。

Gini指数

Gini指数是一种用于衡量数据集纯度的指标，通常用于决策树算法中。在分类问题中，假设有K个类别，数据集D中第k类样本所占的比例为p_k，则Gini指数的计算公式如下：

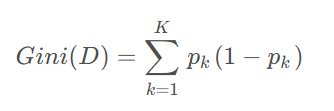
Gini指数衡量的是从数据集D中随机选取两个样本，其类别不一致的概率，因此Gini指数越小，数据集的纯度越高，分类效果越好。与熵类似，Gini指数也是在0到1之间取值，取值越小表示数据集的纯度越高。

在决策树算法中，选择划分特征时，通常会计算每个特征的Gini指数或信息增益，以选取最佳的划分特征。

6.2 信息增益

p1表示样本集合中正例也即猫的比例，wleft指的是占样本的权重，p1 left 代表左枝正例的比例

在决策树算法中，我们希望通过选择最优特征来划分数据集，从而使划分后的数据集更加纯净，即熵减少。而这个熵减少的量就被称为信息增益

信息增益是一种用于衡量一个特征对分类任务的贡献程度的指标，通常用于决策树算法中。在决策树算法中，我们需要在每个节点上选择一个特征，使得选定特征后能够最大程度地提高数据的纯度（即分类的准确性）。信息增益的计算方法是：首先计算数据集的熵，然后计算选定特征后的条件熵，两者相减即为该特征的信息增益。信息增益越大，代表该特征对分类任务的贡献越大。

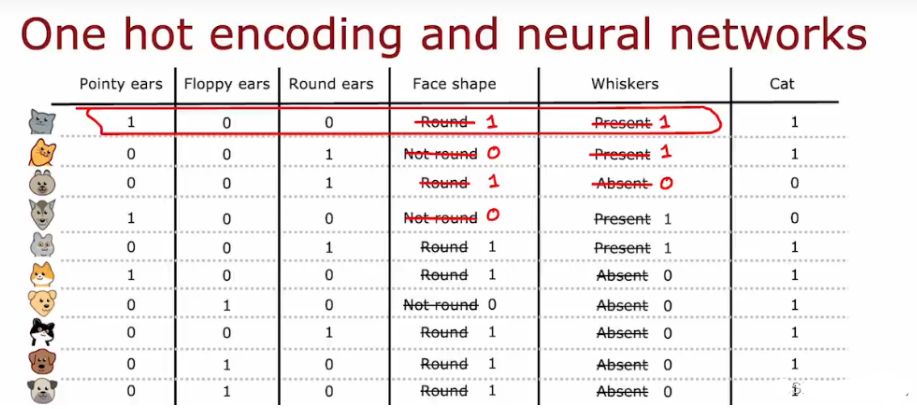
6.3 独热编码One-hot

前面的例子，每个特征只能取两个不同的值，如胡子有、无
，耳朵的尖、椭圆，对于有两个以上的离散值的特征，使用one hot编码

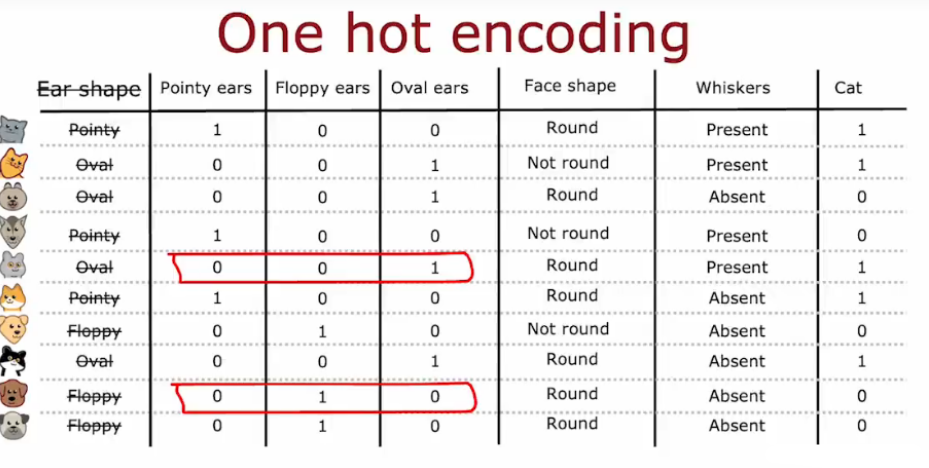
独热编码会将分类特征转换为多维二进制向量，一般适用于当分类特征（较少时）没有自然顺序时，如颜色、城市名称等。
不仅仅适用于决策树，可以对分类特征进行编码，以便作为输入送入神经网络

6.4 当存在连续值特征时

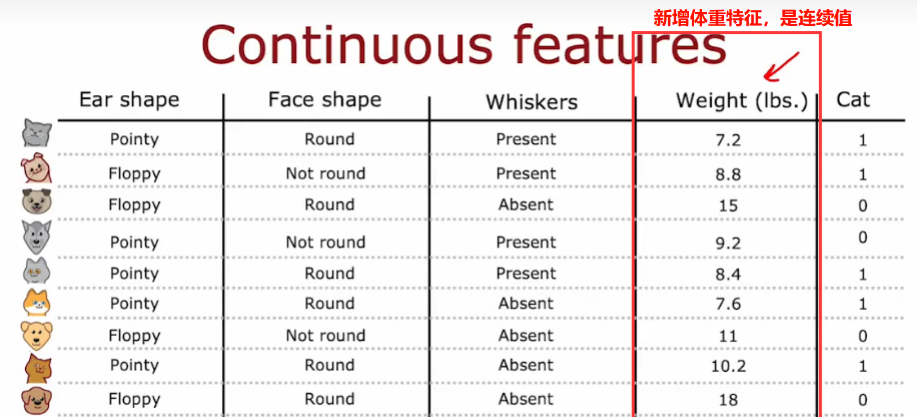
将特征划分，考虑不同的值，计算分隔后的信息增益，选择一个最好的，能获得最好信息增益的那个阈值！一般是对所有的样本排序，根据体重大小排序，取中点值，作为这个阈值的候选值

6.5 回归树 regression tree

泛化到回归问题，预测一个数字，而不是分类问题

eg：

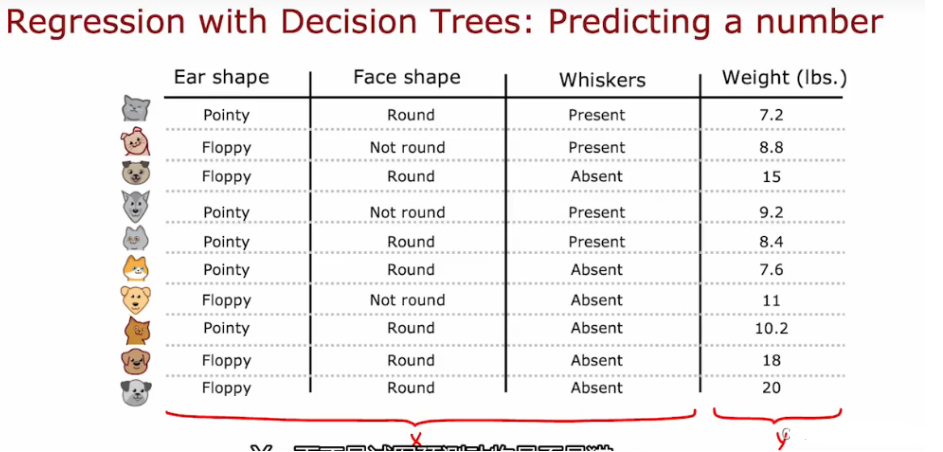
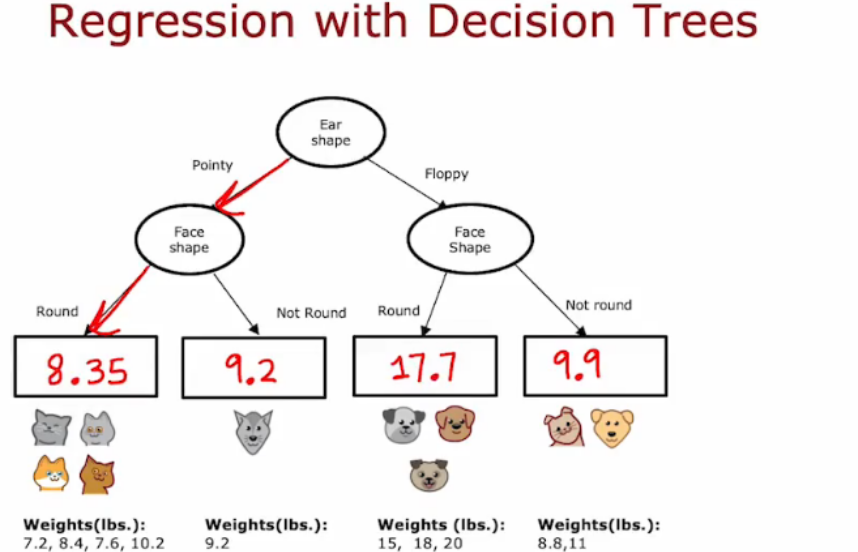
重新选择划分的标准，重新生成

在划分时，不再计算信息增益和纯度，计算减少数据的方差，类似信息增益，我们测量的是方差的减小，选择方差减少最大的那个特征分类标准

6.6 树集合 Tree ensemble

单个决策树受到数据变化的影响很大，导致不同的划分，形成可能不同的树，让算法的鲁棒性变低；
使用树集合，让每一颗树投票。

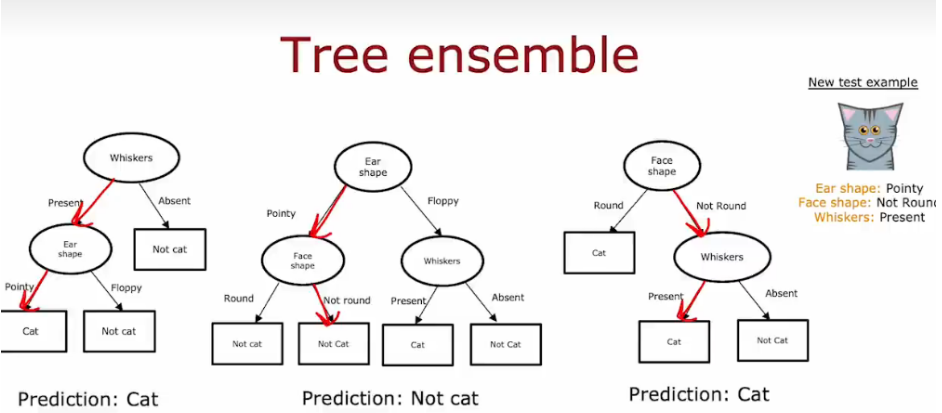
每棵树单独对样本进行预测，然后通过投票机制得出最终的预测结果。
最终，两个“Cat”对一个“Not cat”，通过投票机制，最终的分类结果是“Cat”。

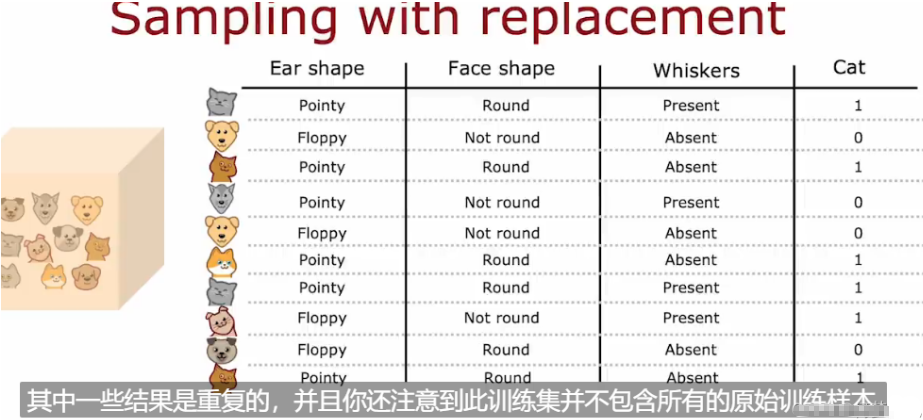
6.6.1 有放回抽样 sampling with replace（构造多个随机的训练集）

构建树集合的方式如下：构建多个随机的训练集，都与我们最初的训练集略有不同

6.6.2 随机森林算法

图中提到，当算法在决策树的每个节点选择用于分裂的特征时，是从个特征中随机选择一个子集，这个子集的大小为 $k$ ，且 。从这k个特征中选收获最大信息增益的特征作为分割特征
图中给出了一个常见的建议，即子集大小的默认值通常设置为特征总数的平方根。

6.6.3 XGBoost

理解boost的思想

此时我们关注的是还没做好的地方，在构建下一个决策树时，把更多的注意力放在做得不好的例子上，不是以相等的(1/m)概率从所有的例子中选取，而是更有可能选取以前训练的树所错误分类的例子。

- 展示了在提升树方法中如何通过有放回抽样（sampling with replacement）来逐步改进模型的过程。
- 在提升树中，不同于随机森林算法中的平等抽样概率，这里会根据样本的难度（即前一轮中被错误分类的样本）来调整抽样概率。
XGBoost extreme gradient boosting 极端梯度提升
- XGBoost的训练过程是一个逐步迭代的过程。它通过不断训练多棵决策树，并使用梯度下降来对每棵树的权重进行优化，以最小化损失函数。
- XGBoost是一种基于梯度提升的强大算法，可以轻松地将XGBoost应用于分类和回归任务中，从而构建高性能的机器学习模型。