lg-dp3
计数的东西有什么特点、转化/好的刻画方式
A Farthest City
题面关键信息:权值为1的最短路 --- bfs --- 分层
那么显然加一个点他只能与上一层连,和一层内部连。则设 \(f_{i,j}\) 为 [点数,最后一层点数]
有
B CSA [1]
题目关键信息:排列。等价于求数的拓扑序个数。
计数对象性质:父亲位置 < 儿子位置
则如果确定根 \(r\) ,那么可以设 \(f_x\) 为 \(x\) 子树中的答案。
本题还有结论为 \(\frac{n!}{\prod sz_x}\)
C [AGC030D] Inversion Sum
计数对象性质:很好维护
其实你要不就是一直维护这个序列(整体来看),要不就是一对一对看。
那么变成概率,再变成期望就很自然了。所以现在我们要求 \(f(i,j)=\mathbf P(a_i>a_j)\)
考虑在交换的时候维护 \(f\) 。
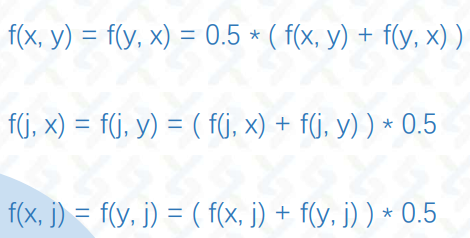
当然不转化可不可以做,是可以的,但是其实很像的。
-
期望有线性性
-
对概率的维护其实融合了所有的情况
D Shopping
题目关键信息:买东西的点必须是连通块
淀粉质可以处理连通块,但是本题也可以按 dfn dp
E [CEOI2016] kangaroo
计数对象特征:波浪形的(wavy);
排列要是波浪形的,最后一个要是 T,第一个要是 S。
考虑连续段 dp,本质上是我们按照某个顺序加数,只确定了相对顺序,然后按照某种方式刻画连续段来维护某种限制。
从小到大加入数,设 \(f_{i,j}\) 表示 [当前加到i,有j段]
此时,有三种方案:
-
新开一段 \(f_{i,j}=(j-[i>S]-[i>T])f_{i-1,j-1}\) (S前面和T后面不能插入段)
-
加在某一段前面/后面 非法(分类讨论一下可以证明)
-
合并两端 \(f_{i,j}=jf_{i-1,j-1}\)
F Tenzing and Random Operations
容易得到式子,但是没啥用,考虑组合意义


这个问题就更具有 dp 多层决策的特征。令 \(f_{i,j}\) 表示 [走过 \(1\to i\),已经用了 \(j\) 个工具]。
那么:
-
不放置新的工具,直接走 \(a_{i+1}f_{i,j}\to f_{i+1,j}\)
-
用获得过的工具,\(jvf_{i,j}\to f_{i+1,j}\)
-
再放置一个工具,\(f_{i,j}\times\frac{i+1}{n}\times(m-j)\times v\to f_{i+1,j+1}\)
G PERIODNI
由于原来这个表格是不规则的,这是不好处理的,考虑划分成若干矩形建笛卡尔树。
在一个小矩形内部的填数方案是容易处理的,对于列的限制,建一棵笛卡尔树,然后做树形 dp 处理。
H Distributing Integers
等价于前面 B 题 CSA
I #(subset sum = K) with Add and Erase
要求动态维护 K 的拆分数。只有加入是很简单的,如果存在删除,我们就强制从 \(-x\) 转移。
可撤销背包,多项式理解方法:
加一个----两项的多项式乘法,删一个----两项的多项式除法。
J [COCI2006-2007#3] BICIKLI
到达不了环就 dp,有环就分讨:
-
若环可以到达2 INF (取反图判断)
-
不可以就不必访问环
K [HNOI2019] 校园旅行
大boss BLACK
\(30\%\)

\(\mathcal O(m^2)\)
\(100\%\)
Hint: 缩减边的数量,使其与点数同级
现在考虑对于两边,我们要做的就是同色来连续子串对应长度相等。
考虑如何能做到。
从变化的角度看,其实对于一个同色联通块来说,它为连入的点提供的能力就在于:
-
如果他是偶环,那么你可以无损地获得任何一个更大的、相同奇偶性连续段,然而如果在保证联通性的同时,即使只有一条边,也可以达到这个目的。
-
如果他是奇环,那么你可以获得改变奇偶性的机会,你可以无损地到达任何一个更大的连续段,如果是这样,那么在保证连通性的时候,连续走一个自环也能达到相同的效果
所以我们可以根据上面的观察削减边数。
本题与下面 H 题等价。 ↩︎