Rank
致敬传奇不挂分 Rank5 模拟赛

A. Mortis
原[ABC302G] Sort from 1 to 4
签,致敬传奇 abc_g 作签到题。
虽然但是还是想了 1h,好在最后成功切了。
具体解释看看题解,求个赞。
点击查看代码
#include<bits/stdc++.h>
using namespace std;const int Ratio=0;
const int N=2e5+5;
int n,ans;
int num[5],to[5][5];
struct rmm{int x,id;}a[N];
bool cmp(rmm a,rmm b){return a.x<b.x;}namespace Wisadel
{short main(){scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&a[i].x),a[i].id=i,num[a[i].x]++;sort(a+1,a+1+n,cmp);// 按元素大小排序for(int i=1;i<=n;i++)if(a[i].id>=1&&a[i].id<=num[1]) to[a[i].x][1]++;else if(a[i].id>=num[1]+1&&a[i].id<=num[1]+num[2]) to[a[i].x][2]++;else if(a[i].id>=num[1]+num[2]+1&&a[i].id<=num[1]+num[2]+num[3]) to[a[i].x][3]++;else if(a[i].id>=num[1]+num[2]+num[3]+1) to[a[i].x][4]++;// 找到所占位置元素值,即连边for(int i=1;i<=4;i++) for(int j=i+1;j<=4;j++){int sum=min(to[i][j],to[j][i]);ans+=sum,to[i][j]-=sum,to[j][i]-=sum;}// 找大小为 2 的环,直接交换int sum=0;for(int i=1;i<=4;i++){int tot=0;for(int j=1;j<=4;j++)if(i!=j&&to[i][j]>0)tot+=to[i][j];ans+=tot,sum=max(sum,tot);// 找环的数量}// 操作的最少次数即为 当前混乱的数的个数-环的数量printf("%d\n",ans-sum);return Ratio;}
}
int main(){return Wisadel::main();}
B. 生活在hzoi上
原[WC2019] 数树 问题 1
致敬传奇 T2 放黑。
虽然但是只是问题 1 应该到不了黑,不过:


跟黑也差不了多少吧www。
C. 嘉然今天吃什么
原[Ynoi Easy Round 2021] TEST_68
致敬传奇 T3 放毒瘤题。
不过好像会了套路还不是很难?
赛时打的 \(\mathcal{O(n^3)}\) 暴力,拿了 10pts,就是先进行一遍 dfs,找到每个点的子树的 dfs 序范围,然后对于每个点,先 \(\mathcal{O(n)}\) 找到除该点子树以外的所有点存起来,然后 \(\mathcal{O(n^2)}\) 暴力找最大异或和。
暴力代码
#include<bits/stdc++.h>
#define fo(x,y,z) for(register int (x)=(y);(x)<=(z);(x)++)
#define fu(x,y,z) for(register int (x)=(y);(x)>=(z);(x)--)
using namespace std;
typedef long long ll;
#define lx ll
inline lx qr()
{char ch=getchar();lx x=0,f=1;for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);return x*f;
}
#undef lx
#define qr qr()
const int Ratio=0;
const int N=2e5+5;
const int mod=998244353;
int n,zct;
int fx[N],L[N],R[N],dfn[N],pos[N],tot;
int hh[N],to[N],ne[N],cnt;
ll a[N],zc[N],ans[N];
namespace Wisadel
{void Wadd(int u,int v){to[++cnt]=v;ne[cnt]=hh[u];hh[u]=cnt;}void Wdfs(int u){dfn[u]=L[u]=++tot,pos[tot]=u;for(int i=hh[u];i!=-1;i=ne[i]){int v=to[i];Wdfs(v);}R[u]=tot;}short main(){// freopen(".in","r",stdin),freopen(".out","w",stdout);n=qr;memset(hh,-1,sizeof hh);fo(i,2,n) fx[i]=qr,Wadd(fx[i],i);fo(i,1,n) a[i]=qr;Wdfs(1);fo(i,1,n){zct=0;fo(j,1,L[i]-1) zc[++zct]=a[pos[j]];fo(j,R[i]+1,tot) zc[++zct]=a[pos[j]];if(!zct){ans[i]=0;continue;}zct=unique(zc+1,zc+1+zct)-zc-1;fo(j,1,zct) fo(k,j+1,zct){ll p=zc[j]^zc[k];if(p>ans[i]) ans[i]=p;}}fo(i,1,n) printf("%lld\n",ans[i]);return Ratio;}
}
int main(){return Wisadel::main();}
求最大异或和,想到 01-trie。开始插入数时直接更新找到全局最大值,并找到最大值对应的一组下标 \(x\) 和 \(y\)。显然,若 \(x\) 和 \(y\) 都不在一个点的子树里,该点答案等于全局最大值,因此,我们只需考虑如何得到 \(x\) 和 \(y\) 所在链上的点答案。
一种可行的办法是,清空 01-trie,进行两次 dfs。从 \(x\) 向上先跳到根节点,根据当时 trie 上的最大值更新该点答案,然后返回前将其所有不在 \(x\) 这条链上的子树内的点加入 trie,最后走到 \(x\) 结束。\(y\) 点同理,记得每次清空 01-trie。
点击查看代码
#include<bits/stdc++.h>
#define fo(x,y,z) for(register int (x)=(y);(x)<=(z);(x)++)
#define fu(x,y,z) for(register int (x)=(y);(x)>=(z);(x)--)
using namespace std;
typedef long long ll;
#define lx ll
inline lx qr()
{char ch=getchar();lx x=0,f=1;for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);return x*f;
}
#undef lx
#define qr qr()
const int Ratio=0;
const int N=5e5+5;
const int mod=998244353;
int n,zct;
int fx[N],hh[N],to[N],ne[N],cnt;
ll a[N],zc[N],maxx;
int tr[N*60][2],pos[N*60],tot=1,ax,ay;
int x,y;
ll mx;
bool yz[N];
namespace Wisadel
{void Wadd(int u,int v){to[++cnt]=v;ne[cnt]=hh[u];hh[u]=cnt;}void Wclear(){fo(i,1,tot) tr[i][0]=tr[i][1]=pos[i]=0;tot=1,mx=0;}void Wins(int i,ll x){int now=1;fu(i,59,0){int tt=(x>>i)&1;if(!tr[now][tt]) tr[now][tt]=++tot;now=tr[now][tt];}pos[now]=i;now=1;fu(i,59,0){int tt=(x>>i)&1;if(tr[now][tt^1]) now=tr[now][tt^1];else if(tr[now][tt]) now=tr[now][tt];else return;}if((x^a[pos[now]])>mx) mx=x^a[pos[now]],ax=i,ay=pos[now];}void Wdfs(int u){Wins(u,a[u]);for(int i=hh[u];i!=-1;i=ne[i]){int v=to[i];Wdfs(v);}}void Wdfss(int u,int fa){if(u==0) return;Wdfss(fx[u],u);zc[u]=mx;yz[u]=1;Wins(u,a[u]);if(u!=fa) for(int i=hh[u];i!=-1;i=ne[i]){int v=to[i];if(v!=fa) Wdfs(v);}}short main(){// freopen(".in","r",stdin),freopen(".out","w",stdout);n=qr;memset(hh,-1,sizeof hh);fo(i,2,n) fx[i]=qr,Wadd(fx[i],i);fo(i,1,n) a[i]=qr,Wins(i,a[i]);x=ax,y=ay,maxx=mx;Wclear();Wdfss(x,x);Wclear();Wdfss(y,y);fo(i,1,n)if(yz[i]) printf("%lld\n",zc[i]);else printf("%lld\n",maxx);return Ratio;}
}
int main(){return Wisadel::main();}
D. APJifengc
原[AGC036D] Negative Cycle
致敬传奇 @APJifengc 小姐的 b20,以及一场模拟赛两道黑。
感觉目前不太可做,粘个题解润了。


末
致敬传奇模拟赛四道题两黑一紫。
以及逆天题目背景
鉴定为万元审完的。
T1
提前祝贺木子米酱赢得本届挺王宝座。

T2
现代OI以APJifengc的“我 b 站 20 粉丝啦”为嚆矢。滥觞于原神与嘉然的期望正失去它们的借鉴意义。但面对看似无垠的未来天空,我想循jijidawang“都人校合。比间多还”好过过早地振翮。
我们怀揣热忱的灵魂天然被赋予对超越性的追求,不屑于古旧坐标的约束,钟情于在别处的芬芳。但当这种期望流于对拜谢主义不假思索的批判,乃至走向真傻逼与cdsidi主义时,便值得警惕了。与秩序的落差、错位向来不能为越矩的行为张本。而纵然我们已有翔实的蓝图,仍不能自持已在浪潮之巅立下了自己的沉锚。
“我是舔狗”Sakura_Lu之言可谓切中了肯綮。人的op性是不可祓除的,而我们欲上青云也无时无刻不在因风借力。嘉然与原神暂且被我们把握为一个薄脊的符号客体,一定程度上是因为我们尚缺乏体验与阅历去支撑自己的认知。而这种偏见的傲慢更远在知性的傲慢之上。
在孜孜矻矻以求OI意义的道路上,对自己的期望本就是在与嘉然与原神对接中塑型的动态过程。而我们的底料便是对不同b20w、不同Delov 的 50w npy的觉感与体认。joke3579为Sakura_Lu送去爆零,又维系你说的对,但是原神。他的OI观念是厚实的,也是实践的。倘若我们在对过往借LYinMX之言“祓魅”后,又对不断膨胀的自我进行“赋魅”,那么在丢失外界预期的同时,未尝也不是丢了自我。
毫无疑问,从原神与嘉然角度一觇的自我有偏狭过时的成分。但我们所应摒弃的不是对此的批判,而是其批判的廉价,其对批判投诚中的反智倾向。在H_Kaguya的观念中,如果在成为狮子与孩子之前,略去了像骆驼一样背负前人遗产的过程,那其“永远重复”洵不能成立。
蓝图上的落差终归只是理念上的区分,在实践场域的分野也未必明晰。譬如当我们追寻文不加点时,在途中涉足挂分,这究竟是伴随着期望的泯灭还是期望的达成?在我们塑造OI的同时,OI也在浇铸我们。既不可否认原生的fst性与衡中牛子性,又承认自己的图景有轻狂的失真,不妨让体验走在言语之前。用不被禁锢的头脑去体味APJifengc的大海与风帆,并效cdsidi,对无法言说之事保持沉默。
用在hzoi上的生活方式体现个体的超越性,保持婞直却又不拘泥于所谓“遗世独立”的单向度形象。这便是LYinMX为我们提供的理想期望范式。生活在hzoi上——始终热爱大地——升上天空。
T3
关注嘉然,顿顿解馋!
T4
原文
我好想做 APJifengc 小姐的 b20 啊。
可是 APJifengc 小姐说她喜欢的是 b20w,我哭了。
我知道既不是 b20 也不是 b20w 的我为什么要哭的。因为我其实是一只多项式。
我从没奢望 APJifengc 小姐能喜欢自己。我明白的,所有人都喜欢理解余裕上手天才打钱的萌萌的 b20 或者 b20w,没有人会喜欢成天 998244353 没人写的多项式。
但我还是问了 APJifengc 小姐:“我能不能做你的 b20?”
我知道我是注定做不了 b20 的。但如果她喜欢 b20,我就可以一直在身边看着她了,哪怕她怀里抱着的永远都是 b20。
可是她说喜欢的是 b20w。
她现在还在看着我,还在逗我开心,是因为 b20w 还没有出现,只有我这多项式每天蹑手蹑脚地从计数题里爬出来,远远地和她对视。
等她喜欢的 b20w 来了的时候,我就该重新滚回我的题库了吧。
但我还是好喜欢她,她能在我还在她身边的时候多看我几眼吗?
APJifengc 小姐说接下来的每个圣诞夜都要和大家一起过。我不知道大家指哪些人。好希望这个集合能够对我做一次胞吞。
b20w 还在害怕 APJifengc 小姐。
我会去把她爱的 b20w 引来的。
我知道稍有不慎,我就会被薄纱。
那时候 APJifengc 小姐大概会把我的身体好好地装起来扔到门外吧。
那我就成了封装好的多项式,嘻嘻。
我希望她能把我扔得近一点,因为我还是好喜欢她。会一直喜欢下去的。
我的灵魂透过窗户向里面看去,挂着的 NTT 在轻轻鸣响, APJifengc 小姐慵懒地靠在沙发上,表演得非常温顺的 b20w 坐在她的肩膀。壁炉的火光照在她的脸庞,我冻僵的原根在风里微微发烫。
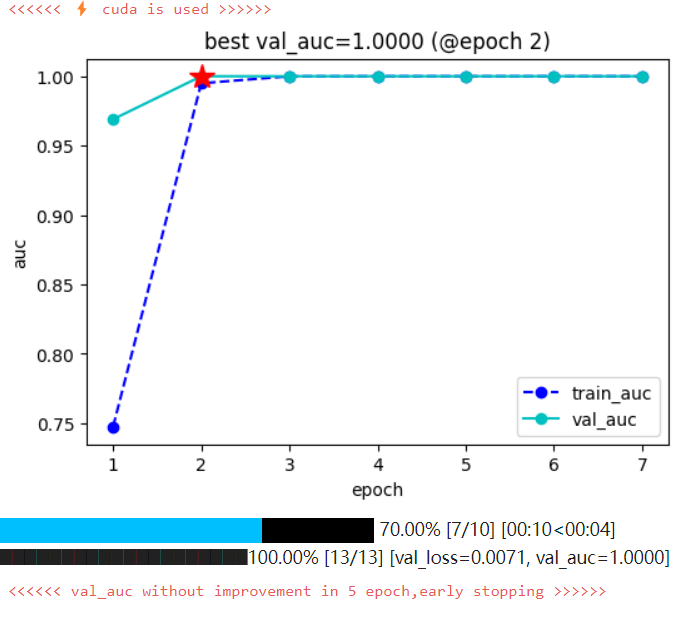
赛时不到 2h 就打了 110pts,后两小时纯坐牢,以为大蓟特蓟了,然后摆+给自己做思想工作,出分一看傻眼了,原来被ex到的不只我。
起码从 T2 还能学到一点新知识:给定 \(n\) 个点一共有 \(n^{n-2}\) 种不同的树。
完结撒花~